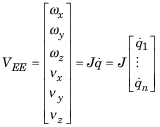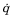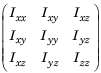geometricJacobian

ロボット コンフィギュレーションの幾何学的ヤコビアン

構文

jacobian = geometricJacobian(robot,configuration,endeffectorname)

説明

jacobian = geometricJacobian(robot,configuration,endeffectorname) は、指定されたエンドエフェクタ名のベースおよびロボット モデルのコンフィギュレーションを基準として幾何学的ヤコビアンを計算します。

例

ロボット コンフィギュレーションの幾何学的ヤコビアン

ロボットの特定のエンドエフェクタおよびコンフィギュレーションの幾何学的ヤコビアンを計算します。

Robotics System Toolbox™ loadrobotから PUMA 560 ロボットを読み込みます。rigidBodyTree オブジェクトとして指定されます。

puma = loadrobot("puma560");

ランダムなコンフィギュレーションのために、Puma ロボット上のボディ "link7" の幾何学的ヤコビアンを計算します。

geoJacob = geometricJacobian(puma,randomConfiguration(puma),"link7")

geoJacob = 6×6

   -0.0000   -0.5752   -0.5752   -0.4266   -0.7683   -0.5213
    0.0000    0.8180    0.8180   -0.3000   -0.3776    0.8377
    1.0000   -0.0000   -0.0000    0.8533   -0.5168    0.1629
    0.1696    0.0823    0.3087   -0.0407    0.0198         0
   -0.5577    0.0578    0.2171   -0.0200    0.0210         0
    0.0000    0.5538    0.2224   -0.0274   -0.0448         0

入力引数

robot — ロボット モデル

rigidBodyTree オブジェクト

ロボット モデル。rigidBodyTree オブジェクトとして指定します。

configuration — ロボット コンフィギュレーション

ベクトル | 構造体

ロボット コンフィギュレーション。ジョイント位置のベクトル、またはロボット モデル内のすべてのボディのジョイント名およびジョイント位置を含む構造体として指定します。コンフィギュレーションは、homeConfiguration(robot)、randomConfiguration(robot) を使用するか、構造体内で独自のジョイント位置を指定することによって生成できます。configuration のベクトル形式を使用するには、robot の DataFormat プロパティを "row" または "column" に設定します。

endeffectorname — エンドエフェクタ名

string スカラー | 文字ベクトル

エンドエフェクタ名。string スカラーまたは文字ベクトルとして指定します。エンドエフェクタは、ロボット モデル内の任意のボディです。

データ型: char | string

出力引数

jacobian — 幾何学的ヤコビアン

6 行 n 列の行列

指定された configuration をもつエンドエフェクタの幾何学的ヤコビアン。6 行 n 列の行列として返されます。ここで n は、ロボットの自由度の数です。ヤコビアンは、ジョイント空間の速度を、ベース座標系に対して相対的に、エンドエフェクタの速度にマッピングします。エンドエフェクタの速度は以下と等価です。

ω は角速度、υ は線形速度、 はジョイント空間の速度です。

詳細

ダイナミクス プロパティ

ロボット ダイナミクスを操作するときは、rigidBody オブジェクトの以下のプロパティを使用してマニピュレーター ロボットの個々のボディの情報を指定します。

• Mass — キログラム単位の剛体の質量。

• CenterOfMass — 剛体の重心位置。[x y z] の形式のベクトルとして指定します。このベクトルは、ボディ座標系を基準とした剛体の重心位置をメートル単位で記述します。オブジェクト関数 centerOfMass は、ロボットの重心を計算する際にこれらの剛体プロパティ値を使用します。

• Inertia — 剛体の慣性。[Ixx Iyy Izz Iyz Ixz Ixy] の形式のベクトルとして指定します。ベクトルは、キログラム平方メートル単位でボディ座標系を基準としています。慣性テンソルは、次の形式の正定値行列です。

  

  Inertia ベクトルの最初の 3 要素は、慣性テンソルの対角要素である慣性モーメントです。最後の 3 要素は、慣性テンソルの非対角要素である慣性乗積です。

マニピュレーター ロボット モデル全体に関連する情報については、以下の rigidBodyTree オブジェクト プロパティを指定します。

• Gravity — ロボットにかかる重力加速度。[x y z] ベクトルとして指定します (m/s²)。既定では重力加速度はありません。

• DataFormat — 運動学およびダイナミクス関数の入出力データ形式。"struct"、"row"、または "column" として指定します。

ダイナミクス方程式

マニピュレーターの剛体ダイナミクスは次の方程式で制御されます。

$$\frac{d}{dt}\left[\begin{array}{c}q\\ \dot{q}\end{array}\right]=\left[\begin{array}{c}\dot{q}\\ M{(q)}^{-1}\left(-C(q,\dot{q})\dot{q}-G(q)-J{(q)}^T{F}_{Ext}+\tau \right)\end{array}\right]$$

次のようにも記述されます。

$$M(q)\ddot{q}=-C(q,\dot{q})\dot{q}-G(q)-J{(q)}^T{F}_{Ext}+\tau$$

ここで、次のようになります。

• $$M(q)$$ — 現在のロボット コンフィギュレーションに基づくジョイント空間の質量行列。この行列はオブジェクト関数 massMatrix を使用して計算します。

• $$C(q,\dot{q})$$ — コリオリ項。$$\dot{q}$$ で乗算され、速度積を計算します。オブジェクト関数 velocityProduct を使用して速度積を計算します。

• $$G(q)$$ — 指定した重力 Gravity の位置を維持するためにすべてのジョイントに必要な重力トルクおよび力。重力トルクはオブジェクト関数 gravityTorque を使用して計算します。

• $$J(q)$$ — 指定したジョイント コンフィギュレーションの幾何学的ヤコビアン。幾何学的ヤコビアンはオブジェクト関数 geometricJacobian を使用して計算します。

• $$F_{Ext}$$ — 剛体にかかる外力の行列。外力はオブジェクト関数 externalForce を使用して生成します。

• $$\tau$$ — 各ジョイントにベクトルとして直接かかるジョイントのトルクと力。

• $$q,\dot{q},\ddot{q}$$ — それぞれ個々のベクトルとしての、ジョイント コンフィギュレーション、ジョイント速度、ジョイント加速度。回転ジョイントの場合は、ラジアン単位 (rad/s と rad/s²) で値をそれぞれ指定します。直進ジョイントの場合は、メートル単位 (m/s と m/s²) で指定します。

ダイナミクスを直接計算するには、オブジェクト関数 forwardDynamics を使用します。この関数は、上記の入力の指定した組み合わせに対してジョイント加速度を計算します。

特定の動きの組み合わせを得るには、オブジェクト関数 inverseDynamics を使用します。この関数は、指定したコンフィギュレーション、速度、加速度、外力を得るために必要なジョイント トルクを計算します。

参照

[1] Featherstone, Roy. Rigid Body Dynamics Algorithms. Springer US, 2008. DOI.org (Crossref), doi:10.1007/978-1-4899-7560-7.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用に関するメモと制限:

rigidBodyTree オブジェクトの作成時には、ロボット モデルにボディを追加する上限として MaxNumBodies を指定する構文を使用します。また、DataFormat プロパティを、名前と値のペアとして指定しなければなりません。次に例を示します。

robot = rigidBodyTree("MaxNumBodies",15,"DataFormat","row")

データの使用量を最小限に抑えるには、上限をモデル内の必要なボディ数に近い数にします。すべてのデータ形式がコード生成用でサポートされています。ダイナミクス関数を使用するには、データ形式を "row" または "column" に設定しなければなりません。

関数 show および showdetails ではコード生成はサポートされません。

バージョン履歴

R2016b で導入

R2024a: 静的なメモリ割り当てのサポート

geometricJacobian で、動的なメモリ割り当てを無効にしたコード生成がサポートされるようになりました。動的なメモリ割り当ての無効化の詳細については、動的メモリ割り当てしきい値の設定 (MATLAB Coder)を参照してください。

参考

getTransform | homeConfiguration | randomConfiguration | rigidBodyJoint | rigidBody

トピック

• Compute Joint Torques To Balance An Endpoint Force and Moment