深層学習を使用した転動体ベアリングの故障診断

この例では次を使用します。

この例では、深層学習の手法を使用して、転動体ベアリングの故障診断を行う方法を説明します。例では、1-D ベアリング振動信号をスカログラムの 2-D イメージに変換し、事前学習済みのネットワークを使用して転移学習を適用することにより、ベアリングの故障を分類する方法を示します。転移学習は、従来のベアリング診断手法において特徴の抽出と特徴の選択に要した時間を大幅に短縮し、この例で使用される小規模な MFPT データセットに対し良好な精度を提供します。

この例を実行するには、https://github.com/mathworks/RollingElementBearingFaultDiagnosis-Data に移動し、リポジトリ全体を ZIP ファイルとしてダウンロードして、ライブスクリプトと同じディレクトリに保存してください。

転動体ベアリングの故障

転動体ベアリングにおける局所的な故障は、外輪、内輪、ケージ、または転動体に発生する可能性があります。転動体が外輪または内輪上の局所的な故障部位に当たるか、転動体上の故障が外輪や内輪に当たると、ベアリングと応答変換器間に高周波共振が励起されます [1]。次の図は、転動体が内輪にある局所的な故障部位に当たる様子を示しています。一般的に、こうした故障を検出し識別することが問題となります。

Machinery Failure Prevention Technology (MFPT) Challenge データ

MFPT Challenge データ [2] には、さまざまな故障状態下でマシンから収集された 23 のデータセットが含まれています。最初の 20 のデータセットはベアリングテストリグから収集したもので、良好な状態が 3 つ、一定負荷での外輪の故障が 3 つ、さまざまな負荷での外輪の故障が 7 つ、さまざまな負荷での内輪の故障が 7 つ含まれています。残りの 3 つのデータセットは実際のマシン (オイルポンプベアリング、中速ベアリング、および遊星ベアリング) からのものです。故障の場所は不明です。この例では、既知の状態でテストリグから収集されたデータのみを使用します。

各データセットには、加速度信号 gs、サンプリングレート sr、シャフト回転数 rate、負荷の重み load、および異なる故障箇所を表す 4 つの臨界周波数である外輪転動体通過周波数 (BPFO)、内輪転動体通過周波数 (BPFI)、基本トレーン周波数 (FTF)、および転動体スピン周波数 (BSF) が含まれます。BPFO と BPFI の式は、以下のとおりです [1]。

BPFO:

$B P F O = \frac{n f_{r}}{2} (1 - \frac{d}{D} \cos ϕ)$

BPFI:

$B P F I = \frac{n f_{r}}{2} (1 + \frac{d}{D} \cos ϕ)$

図に示されるように、 $d$ はボールの直径、 $D$ はピッチの直径です。変数 $f_{r}$ はシャフト回転数、 $n$ は転動体の数、 $ϕ$ はベアリングの接触角です [1]。

ベアリングデータのスカログラム

事前学習済みの CNN 深層ネットワークを活用するために、補助関数 plotBearingSignalAndScalogram を使用して、MFPT データセットの 1-D 振動信号を 2-D スカログラムに変換します。スカログラムは、元の時間領域信号の、時間-周波数領域での表現です [3]。スカログラムイメージの 2 つの次元は、時間と周波数を表します。スカログラムと元の振動信号との関係を可視化するために、内輪故障に伴う振動信号を、そのスカログラムと並べてプロットします。

% Import data with inner race fault
data_inner = load(fullfile(matlabroot, 'toolbox', 'predmaint', ...
    'predmaintdemos', 'bearingFaultDiagnosis', ...
    'train_data', 'InnerRaceFault_vload_1.mat'));
% Plot bearing signal and scalogram
plotBearingSignalAndScalogram(data_inner)

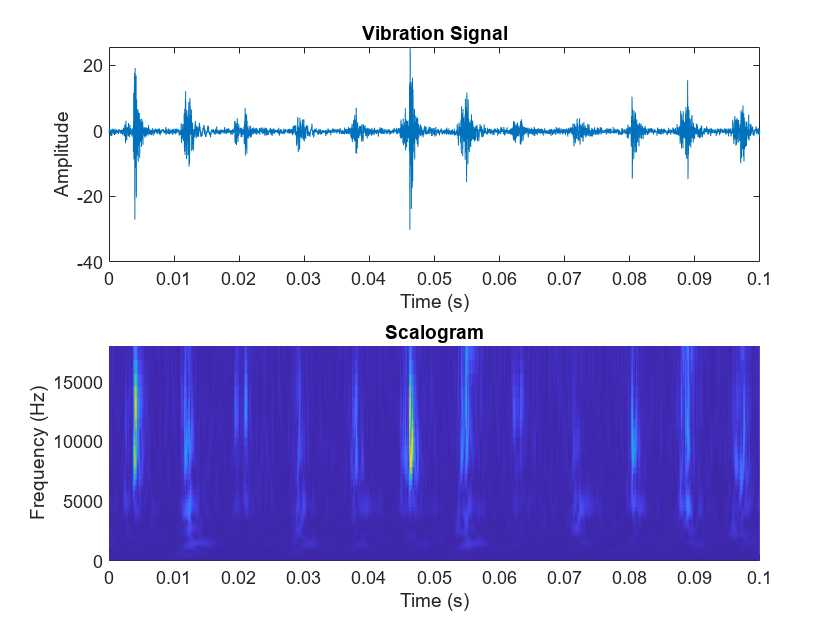
Figure contains 2 axes objects. Axes object 1 with title Vibration Signal, xlabel Time (s), ylabel Amplitude contains an object of type line. Axes object 2 with title Scalogram, xlabel Time (s), ylabel Frequency (Hz) contains an object of type surface.

テストされたベアリングの BPFI は 118.875 Hz であるため、プロットに表示されている 0.1 秒間で、振動信号には 12 のインパルスが含まれています。これに応じて、スカログラムには、振動信号のインパルスと揃った 12 の明確なピークが表示されています。次に、外輪故障のスカログラムを可視化します。

% Import data with outer race fault
data_outer = load(fullfile(matlabroot, 'toolbox', 'predmaint', ...
    'predmaintdemos', 'bearingFaultDiagnosis', ...
    'test_data', 'OuterRaceFault_3.mat'));
% Plot original signal and its scalogram
plotBearingSignalAndScalogram(data_outer)

外輪故障のスカログラムには、最初の 0.1 秒間に 8 つの明確なピークが表示され、これは、転動体通過周波数と一貫しています。時間領域信号のインパルスは、内輪故障の場合ほど圧倒的ではないため、スカログラムの明確なピークが示すバックグランドとのコントラストは弱くなっています。通常状態のスカログラムには、圧倒的に明確なピークは見られません。

% Import normal bearing data
data_normal = load(fullfile(matlabroot, 'toolbox', 'predmaint', ...
    'predmaintdemos', 'bearingFaultDiagnosis', ...
    'train_data', 'baseline_1.mat'));
% Plot original signal and its scalogram
plotBearingSignalAndScalogram(data_normal)

明確なピークの数は、内輪故障、外輪故障、および通常状態を区別するための優れた特徴です。そのため、スカログラムはベアリングの故障の分類によく適した候補となり得ます。この例では、ベアリング信号の測定値はすべて、同じシャフト回転数を使用したテストからのものです。この例を、異なったシャフト回転数でのベアリング信号に適用するには、データをシャフト回転数によって正規化する必要があります。そうしない場合、スカログラムの "柱" の数は誤ったものとなります。

学習データの準備

ダウンロードしたファイルを解凍します。

if exist('RollingElementBearingFaultDiagnosis-Data-master.zip', 'file')
    unzip('RollingElementBearingFaultDiagnosis-Data-master.zip')
end

ダウンロードしたデータセットには、14 の MAT ファイル (正常 2 つ、内輪故障 5 つ、外輪故障 7 つ) からなる学習データセットと、6 つの MAT ファイル (正常 1 つ、内輪故障 2 つ、外輪故障 3 つ) からなるテストデータセットが含まれています。

ReadFcn に関数ハンドルを割り当てることで、ファイルアンサンブルのデータストアがファイル内に移動してデータを必要な形式で取得できるようになります。たとえば、MFPT データには構造体 bearing があり、これは振動信号 gs、サンプリングレート sr、その他を含みます。構造体 bearing そのものを返す代わりに、ファイルアンサンブルのデータストアがデータ構造体 bearing 内にある振動信号 gs を返すように、関数 readMFPTBearing は記述されています。

fileLocation = fullfile('.', 'RollingElementBearingFaultDiagnosis-Data-master', 'train_data');
fileExtension = '.mat';
ensembleTrain = fileEnsembleDatastore(fileLocation, fileExtension);
ensembleTrain.ReadFcn = @readMFPTBearing;
ensembleTrain.DataVariables = ["gs", "sr", "rate", "load", "BPFO", "BPFI", "FTF", "BSF"];
ensembleTrain.ConditionVariables = ["Label", "FileName"];
ensembleTrain.SelectedVariables = ["gs", "sr", "rate", "load", "BPFO", "BPFI", "FTF", "BSF", "Label", "FileName"]

ensembleTrain = 
  fileEnsembleDatastore with properties:

                 ReadFcn: @readMFPTBearing
        WriteToMemberFcn: []
           DataVariables: [8×1 string]
    IndependentVariables: [0×0 string]
      ConditionVariables: [2×1 string]
       SelectedVariables: [10×1 string]
                ReadSize: 1
              NumMembers: 14
          LastMemberRead: [0×0 string]
                   Files: [14×1 string]

ここで、1-D 振動信号をスカログラムに変換し、イメージを学習用に保存します。各スカログラムのサイズは 227 x 227 x 3 で、SqueezeNet で必要とされる入力サイズと同じです。精度を上げるために、補助関数 convertSignalToScalogram は生の信号を囲み、複数のセグメントに分割します。以下のコマンドを実行した後、"train_image" という名前のフォルダーが現在のフォルダー内に表示されます。"RollingElementBearingFaultDiagnosis-Data-master/train_data" フォルダーにあるベアリング信号のスカログラムイメージは、すべて "train_image" フォルダーに保存されます。

reset(ensembleTrain)
while hasdata(ensembleTrain)
  folderName = 'train_image';
  convertSignalToScalogram(ensembleTrain,folderName);
end

イメージデータストアを作成し、"train_image" フォルダーのイメージの 80% を学習用に、20% を検証用に使用するよう、学習データを学習と検証のデータセットに分割します。

% Create image datastore to store all training images
path = fullfile('.', folderName);
imds = imageDatastore(path, ...
  'IncludeSubfolders',true,'LabelSource','foldernames');
% Use 20% training data as validation set
[imdsTrain,imdsValidation] = splitEachLabel(imds,0.8,'randomize');

転移学習によるネットワークの学習

次に、事前学習済みの SqueezeNet 畳み込みニューラルネットワークを微調整して、スカログラムに対し分類を実行します。SqueezeNet は 100 万を超えるイメージで学習しており、豊富な特徴表現を学んでいます。転移学習は、深層学習アプリケーションで広く使用されています。事前学習済みのネットワークを選び、それを新しいタスクの開始点として使用できます。ネットワークを転移学習を使って微調整するのは、通常、ランダムに初期化された重みを使ってゼロからネットワークに学習させるよりもはるかに速くて簡単です。比較的少数の学習イメージを使用して、学習済みの特徴をすばやく転移させることができます。SqueezeNet ネットワークを読み込んで表示します。

net = imagePretrainedNetwork("squeezenet")

net = 
  dlnetwork with properties:

         Layers: [68×1 nnet.cnn.layer.Layer]
    Connections: [75×2 table]
     Learnables: [52×3 table]
          State: [0×3 table]
     InputNames: {'data'}
    OutputNames: {'prob_flatten'}
    Initialized: 1

  View summary with summary.

analyzeNetwork(net)

SqueezeNet では、畳み込み層 'conv10' を使用してイメージの特徴を抽出し、入力イメージを分類します。この層には、特徴を組み合わせるための情報が含まれており、ネットワークはそれを抽出してクラスの確率、損失値、および予測されるラベルを生成します。SqueezeNet を新たなイメージの分類用に再度学習させるには、畳み込み層 'conv10' を、ベアリングのイメージに適応した新しい層に置き換える必要があります。

ほとんどのネットワークで、学習可能な重みをもつ最終層は全結合層です。SqueezeNet などの一部のネットワークでは、これと異なり、最終の学習可能な層は 1 行 1 列の畳み込み層となっています。ここでは、畳み込み層を、フィルター数がクラス数と等しい新たな畳み込み層に置き換えます。

numClasses = numel(categories(imdsTrain.Labels));

newConvLayer = convolution2dLayer([1, 1],numClasses,'WeightLearnRateFactor',10,'BiasLearnRateFactor',10,"Name",'new_conv');
net = replaceLayer(net,'conv10',newConvLayer);

学習オプションを指定します。転移された層での学習速度を下げるため、初期学習率を小さな値に設定します。畳み込み層を作成する際には、より高い学習率係数を含めることで、新しい最終層での学習速度を高めます。学習率設定のこの組み合わせの結果、新しい層でのみ学習が速くなり、他の層での学習はより遅くなります。転移学習を実行する場合、さほど多くのエポックで学習させる必要はありません。エポックは、学習データセット全体での 1 回の完全な学習サイクルです。ソフトウェアは学習の間、ValidationFrequency 回の反復ごとにネットワークを検証します。

options = trainingOptions('sgdm', ...
  'InitialLearnRate',0.0001, ...
  'MaxEpochs',4, ...
  'Shuffle','every-epoch', ...
  'ValidationData',imdsValidation, ...
  'ValidationFrequency',30, ...
  'Verbose',false, ...
  'MiniBatchSize',20, ...
  'Plots','training-progress');

新しいネットワークを学習させ、損失関数を 'crossentropy' ( に設定します (分類問題の場合)。既定では、Parallel Computing Toolbox™ およびサポートされている GPU デバイスがある場合、trainnet は GPU を使用します。サポートされているデバイスの詳細については、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。それ以外の場合、trainnet は CPU を使用します。また、trainingOptions の名前と値の引数 'ExecutionEnvironment' を使用して実行環境を指定することもできます。

net = trainnet(imdsTrain,net,"crossentropy",options);

テストデータセットを使用した検証

"RollingElementBearingFaultDiagnosis-Data-master/test_data" フォルダーにあるベアリング信号を使用して、学習済みネットワークの精度を検証します。テストデータは、学習データと同じ方法で処理する必要があります。

ベアリングの振動信号を格納するためのファイルアンサンブルデータストアをテストフォルダーに作成します。

fileLocation = fullfile('.', 'RollingElementBearingFaultDiagnosis-Data-master', 'test_data');
fileExtension = '.mat';
ensembleTest = fileEnsembleDatastore(fileLocation, fileExtension);
ensembleTest.ReadFcn = @readMFPTBearing;
ensembleTest.DataVariables = ["gs", "sr", "rate", "load", "BPFO", "BPFI", "FTF", "BSF"];
ensembleTest.ConditionVariables = ["Label", "FileName"];
ensembleTest.SelectedVariables = ["gs", "sr", "rate", "load", "BPFO", "BPFI", "FTF", "BSF", "Label", "FileName"];

1-D 信号を 2-D スカログラムに変換します。

reset(ensembleTest)
while hasdata(ensembleTest)
  folderName = 'test_image';
  convertSignalToScalogram(ensembleTest,folderName);
end

テストイメージを格納するためのイメージデータストアを作成します。

path = fullfile('.','test_image');
imdsTest = imageDatastore(path, ...
  'IncludeSubfolders',true,'LabelSource','foldernames');

学習済みネットワークを使ってテストイメージデータストアを分類します。

scores = minibatchpredict(net,imdsTest,'MiniBatchSize',20);
YPred = scores2label(scores,unique(imdsTrain.Labels));

予測の精度を計算します。

YTest = imdsTest.Labels;
accuracy = sum(YPred == YTest)/numel(YTest)

accuracy = 0.9807

混同行列をプロットします。

figure
confusionchart(YTest,YPred)

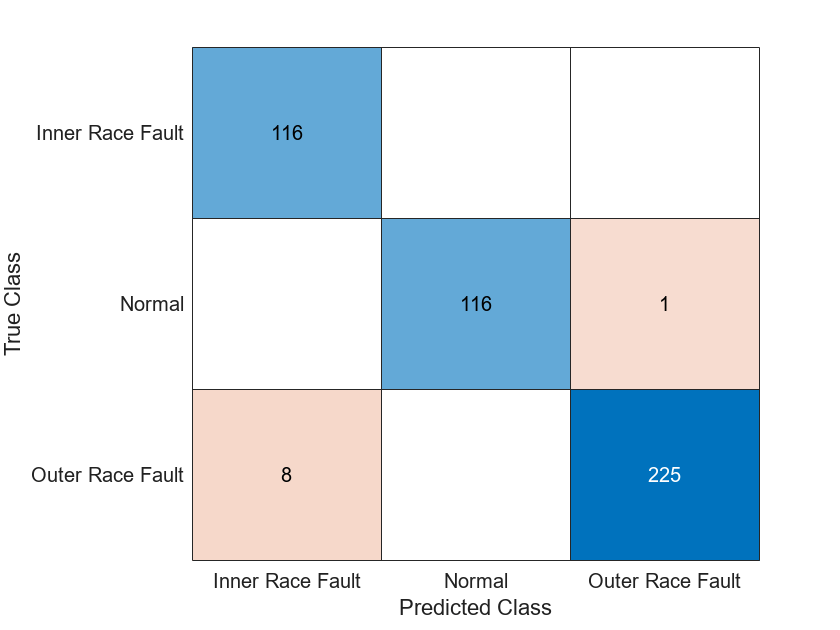
Figure contains an object of type ConfusionMatrixChart.

ネットワークに複数回学習させる場合、学習ごとに精度にいくらかの変動が見られることもありますが、平均精度は約 98% になるはずです。学習セットは極めて小さなものですが、この例では転移学習の利点を生かして、優れた精度が達成されています。

まとめ

この例は、転動体ベアリングのさまざまな故障タイプを特定するうえで、データサイズが比較的小さい場合でも、深層学習が効果的なツールであり得ることを示しています。深層学習の手法により、従来の手法で特徴量エンジニアリングに必要とされる時間が短縮されます。比較については、転動体ベアリングの故障診断の例を参照してください。

参考文献

[1] Randall, Robert B., and Jérôme Antoni. "Rolling Element Bearing Diagnostics—A Tutorial." Mechanical Systems and Signal Processing 25, no. 2 (February 2011): 485–520. https://doi.org/10.1016/j.ymssp.2010.07.017.

[2] Bechhoefer, Eric. "Condition Based Maintenance Fault Database for Testing Diagnostics and Prognostic Algorithms."2013. https://www.mfpt.org/fault-data-sets/.

[3] Verstraete, David, Andrés Ferrada, Enrique López Droguett, Viviana Meruane, and Mohammad Modarres. "Deep Learning Enabled Fault Diagnosis Using Time-Frequency Image Analysis of Rolling Element Bearings." Shock and Vibration 2017 (2017): 1–17. https://doi.org/10.1155/2017/5067651.

補助関数

function plotBearingSignalAndScalogram(data)
% Convert 1-D bearing signals to scalograms through wavelet transform
fs = data.bearing.sr;
t_total = 0.1; % seconds
n = round(t_total*fs);
bearing = data.bearing.gs(1:n);
[cfs,frq] = cwt(bearing,'amor', fs);

% Plot the original signal and its scalogram
figure
subplot(2,1,1)
plot(0:1/fs:(n-1)/fs,bearing)
xlim([0,0.1])
title('Vibration Signal')
xlabel('Time (s)')
ylabel('Amplitude')
subplot(2,1,2)
surface(0:1/fs:(n-1)/fs,frq,abs(cfs))
shading flat
xlim([0,0.1])
ylim([0,max(frq)])
title('Scalogram')
xlabel('Time (s)')
ylabel('Frequency (Hz)')
end

function convertSignalToScalogram(ensemble,folderName)
% Convert 1-D signals to scalograms and save scalograms as images
data = read(ensemble);
fs = data.sr;
x = data.gs{:};
label = char(data.Label);
fname = char(data.FileName);
ratio = 5000/97656;
interval = ratio*fs;
N = floor(numel(x)/interval);

% Create folder to save images
path = fullfile('.',folderName,label);
if ~exist(path,'dir')
  mkdir(path);
end

for idx = 1:N
  sig = envelope(x(interval*(idx-1)+1:interval*idx));
  cfs = cwt(sig,'amor', seconds(1/fs));
  cfs = abs(cfs);
  img = ind2rgb(round(rescale(flip(cfs),0,255)),jet(320));
  outfname = fullfile('.',path,[fname '-' num2str(idx) '.jpg']);
  imwrite(imresize(img,[227,227]),outfname);
end
end