境界値問題
常微分方程式の境界値問題のソルバー
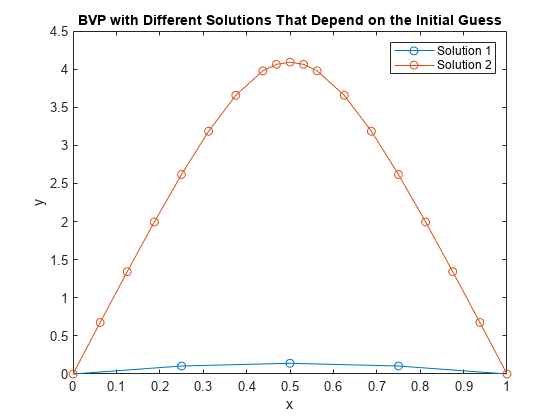
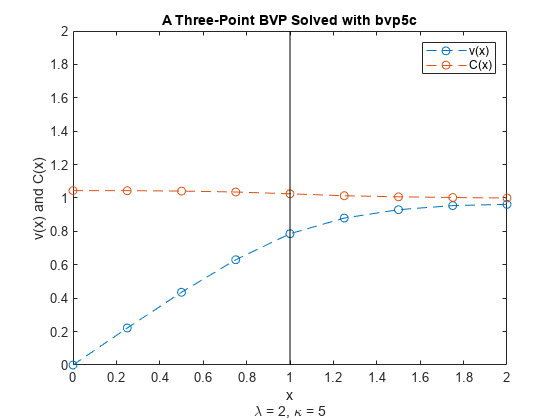
境界値問題 (BVP) は、境界条件に依存する常微分方程式です。初期値問題とは異なり、BVP には有限解がある場合、解がない場合、または解が無限に存在する場合があります。解の初期推定は BVP の求解に不可欠であり、推定の質はソルバーのパフォーマンスや、ときには問題が解けるかどうかにも大きく影響します。bvp4c ソルバーと bvp5c ソルバーは、2 点境界条件、多点条件、解の特異性、または未知のパラメーターをもつ境界値問題を扱います。詳細については、境界値問題の求解を参照してください。
関数
トピック
- 境界値問題の求解
背景情報、ソルバーの機能、アルゴリズム、例の概要。