複数の境界条件をもつ BVP を解く
この例では、多点境界値問題を解く方法、求める解が積分区間内のどこで条件を満たすかについて説明します。
における について、次の方程式を考えます。
,
.
問題の既知のパラメーターは 、、、および です。
の方程式の項 は で滑らかではないため、問題を直接解くことはできません。代わりに、問題を 2 つに分割できます。1 つは区間 に、もう 1 つは区間 に設定します。2 つの領域間の接続については、解が で連続的でなければなりません。解は次の境界条件も満たさなければなりません。
,
.
各領域の方程式は次のようになります。
領域 1:
,
.
領域 2:
,
.
境界点 は両方の領域に含まれています。この点では、ソルバーは "左" と "右" 両方の解を生成します。これらの解は、解の連続性を確保するために等しくなければなりません。
MATLAB® でこの連立方程式を解くには、方程式、境界条件、および初期推定をコード化してから、境界値問題ソルバー bvp5c を呼び出す必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。
方程式のコード作成
および の方程式は、解かれる領域によって異なります。多点境界値問題の場合、導関数は 3 番目の入力引数 region を受け入れなければなりません。この入力引数は、導関数が評価されている領域を特定するために使用されます。ソルバーは左から右の領域に 1 から始まる番号を付けます。
シグネチャ dydx = f(x,y,region,p) を使用して方程式をコード化する関数を作成します。ここでは以下のようになります。
xは独立変数です。yは従属変数です。dydx(1)によって の方程式が与えられ、dydx(2)によって の方程式が与えられます。regionは、導関数が計算されている領域の番号です (この 2 領域の問題では、regionは1または2です)。pは定数パラメーター の値を含むベクトルです。
switch ステートメントを使用して、解かれる領域に応じて異なる方程式を返します。関数は次のようになります。
function dydx = f(x,y,region,p) % equations being solved n = p(1); eta = p(4); dydx = zeros(2,1); dydx(1) = (y(2) - 1)/n; switch region case 1 % x in [0 1] dydx(2) = (y(1)*y(2) - x)/eta; case 2 % x in [1 lambda] dydx(2) = (y(1)*y(2) - 1)/eta; end end
メモ: 関数はすべて例の最後にローカル関数として含まれます。
境界条件のコード化
2 つの領域で 2 つの 1 次微分方程式を解くには、4 つの境界条件が必要です。これらの条件のうち次の 2 つは元の問題から取得します。
,
.
残りの 2 つの条件は、境界点 で左と右の解の連続性を適用します。
,
.
多点境界値問題の境界条件関数の引数 YL と YR は行列になります。特に k 番目の列 YL(:,k) は、k 番目の領域の左側の境界における解です。同様に YR(:,k) は、k 番目の領域の右側の境界での解です。
この問題では、 は YL(:,1) によって近似され、 は YR(:,end) によって近似されます。 における解の連続性では、YR(:,1) = YL(:,2) であることが求められます。
4 つの境界条件の残差値をエンコードする関数は次のようになります。
function res = bc(YL,YR) res = [YL(1,1) % v(0) = 0 YR(1,1) - YL(1,2) % Continuity of v(x) at x=1 YR(2,1) - YL(2,2) % Continuity of C(x) at x=1 YR(2,end) - 1]; % C(lambda) = 1 end
初期推定の作成
多点境界値問題の場合、境界条件は積分区間の始まりと終わりに自動的に適用されます。ただし、他の境界点では double エントリを xmesh に指定しなければなりません。境界条件を満たす単純な推定は定数の推定 y = [1; 1] です。
xc = 1; xmesh = [0 0.25 0.5 0.75 xc xc 1.25 1.5 1.75 2]; yinit = [1; 1]; sol = bvpinit(xmesh,yinit);
方程式の求解
定数パラメーターの値を定義し、それをベクトル p に入れます。構文 @(x,y,r) f(x,y,r,p) を使用して bvp5c に関数を提供して、パラメーターのベクトルを提供します。
各解を次の解に対する初期推定として使用して、 のいくつかの値について解を計算します。 の各値に対して、浸透圧濃度 の値を計算します。ループの各反復で、計算された値と近似解析解を比較します。
lambda = 2; n = 5e-2; for kappa = 2:5 eta = lambda^2/(n*kappa^2); p = [n kappa lambda eta]; sol = bvp5c(@(x,y,r) f(x,y,r,p), @bc, sol); K2 = lambda*sinh(kappa/lambda)/(kappa*cosh(kappa)); approx = 1/(1 - K2); computed = 1/sol.y(1,end); fprintf(' %2i %10.3f %10.3f \n',kappa,computed,approx); end
2 1.462 1.454 3 1.172 1.164 4 1.078 1.071 5 1.039 1.034
解のプロット
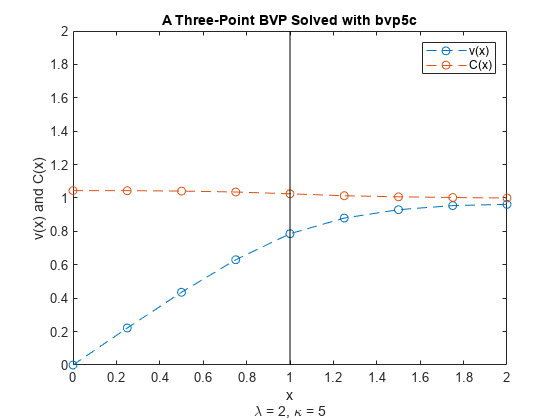
と に対する解要素と、境界点 での垂直線をプロットします。 の表示された解は、ループの最終反復から生じたものです。
plot(sol.x,sol.y(1,:),'--o',sol.x,sol.y(2,:),'--o') line([1 1], [0 2], 'Color', 'k') legend('v(x)','C(x)') title('A Three-Point BVP Solved with bvp5c') xlabel({'x', '\lambda = 2, \kappa = 5'}) ylabel('v(x) and C(x)')
ローカル関数
ここでは、BVP ソルバー bvp5c が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。
function dydx = f(x,y,region,p) % equations being solved n = p(1); eta = p(4); dydx = zeros(2,1); dydx(1) = (y(2) - 1)/n; switch region case 1 % x in [0 1] dydx(2) = (y(1)*y(2) - x)/eta; case 2 % x in [1 lambda] dydx(2) = (y(1)*y(2) - 1)/eta; end end %------------------------------------------- function res = bc(YL,YR) % boundary conditions res = [YL(1,1) % v(0) = 0 YR(1,1) - YL(1,2) % Continuity of v(x) at x=1 YR(2,1) - YL(2,2) % Continuity of C(x) at x=1 YR(2,end) - 1]; % C(lambda) = 1 end %-------------------------------------------