bvpinit

境界値問題ソルバー用の初期推定の作成

構文

solinit = bvpinit(x,yinit)

solinit = bvpinit(sol,[anew bnew])

solinit = bvpinit(___,parameters)

説明

solinit = bvpinit(x,yinit) は、初期メッシュ x と解の初期推定 yinit を使用して、境界値問題の初期推定解を作成します。その後、初期推定 solinit を bvp4c または bvp5c の入力の 1 つとして使用し、境界値問題を解きます。

solinit = bvpinit(sol,[anew bnew]) は、区間 [anew bnew] で解の初期推定を形成します。ここで、sol は bvp4c または bvp5c から得られる解の構造体です。新しい区間 [anew bnew] は、sol が定義されている前の区間より大きくなければなりません。前の解 sol は新しい区間に外挿されます。

solinit = bvpinit(___,parameters) は、境界値問題で未知の値を含むパラメーターの初期推定のベクトルを指定します。この構文は、前述のいずれかの入力引数の組み合わせと共に使用できます。

例

BVP 解の初期推定

BVP の解の初期推定を作成し、BVP を bvp4c で解いてから、解を新しい領域に拡張します。

BVP 問題の解の良好な初期推定を作成することは、おそらく問題を解く上で最も難しい部分です。BVP の解は必ずしも一意でないため、初期推定は、多くの解のうちソルバーがいずれを返すかを決める要因になる場合があります。初期推定は境界条件を満たす必要があります。また、中間の挙動は問題に関する全体的な想定を反映する必要があります (解は振動するかどうか、単純な線形関数であるかどうかなど)。

次の微分方程式を考慮します。

$${{\mathit{y}}^{\prime }}^{\prime }=-\mathit{y}$$.

この方程式は次の境界条件に従います。

$\mathit{y}\left(0\right)=\mathit{y}\left(\pi \right)=0$.

この方程式を 1 次系としてコード化する関数は次のとおりです。

function dydx = bvpfun(x,y)
dydx = [y(2)
       -y(1)];
end

同様に、境界条件をコード化する関数は次のとおりです。

function res = bcfun(ya,yb)
res = [ya(1)
       yb(1)];
end

(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB® パスのディレクトリに保存することもできます。

関数ハンドルによる初期推定

方程式の解が振動する可能性は十分あるため、解の挙動と、固定境界点間の導関数の挙動として、正弦関数と余弦関数は良好な初期推定です。

function y = guess(x)
y = [sin(x)
     cos(x)];
end

領域 $\left[0,\pi \right]$ にある等間隔のメッシュ点 10 点と初期推定関数を使用して、解の構造体を作成します。

xmesh = linspace(0,pi,10);
solinit = bvpinit(xmesh,@guess);

BVP の求解

ODE 関数、境界条件および解の推定を使用して bvp4c を呼び出します。結果をプロットします。

sol = bvp4c(@bvpfun, @bcfun, solinit);
plot(sol.x,sol.y,'-o')

ローカル関数

ここでは、BVP ソルバー bvp4c が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function dydx = bvpfun(x,y) % equation being solved
dydx = [y(2)
       -y(1)];
end
%-------------------------------------------
function res = bcfun(ya,yb) % boundary conditions
res = [ya(1)
       yb(1)];
end
%-------------------------------------------
function y = guess(x) % guess at solution behavior
y = [sin(x)
     cos(x)];
end
%-------------------------------------------

外挿による BVP の解の拡張

初期区間で BVP を解き、それぞれの解を次の区間の初期推定として使用して区間を繰り返し拡張します。

次の方程式を考えます。

${{\mathit{y}}^{\prime }}^{\prime }=\mathit{y}$.

この方程式は次の 2 つの方程式からなる連立 1 階微分方程式になります。

${{\mathit{y}}_1}^{\prime }={\mathit{y}}_2$,

${{\mathit{y}}_2}^{\prime }={\mathit{y}}_1$.

この方程式は、区間 $\left[0,3\right]$ で初期定義され、次の境界条件に従います。

$\mathit{y}\left(0\right)=0$,

$\mathit{y}\left(3\right)=1$.

この方程式を 1 次系としてコード化する関数は次のとおりです。

function dydx = bvpfun(x,y)
dydx = [y(2)
        y(1)];
end

同様に、境界条件をコード化する関数は次のとおりです。

function res = bcfun(ya,yb)
res = [ya(1)
       yb(1)-1];
end

(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

初期推定

指数関数を解の初期推定として使用します。この方程式には 2 つの解の成分があるため、ベクトルを返す y = guess(x) の形式の初期推定関数を作成します。

function y = guess(x)
y = [exp(x)
     exp(x)];
end

5 点からなるメッシュは、推定関数の挙動を十分にキャプチャできます。

xmesh = linspace(0,3,5);
solinit = bvpinit(xmesh,@guess);

方程式の求解

初期区間 $\left[0,3\right]$ で方程式を解き、${\mathit{y}}_1$ に関する結果をプロットします。

sol = bvp4c(@bvpfun, @bcfun, solinit);
plot(sol.x(1,:),sol.y(1,:),'-o')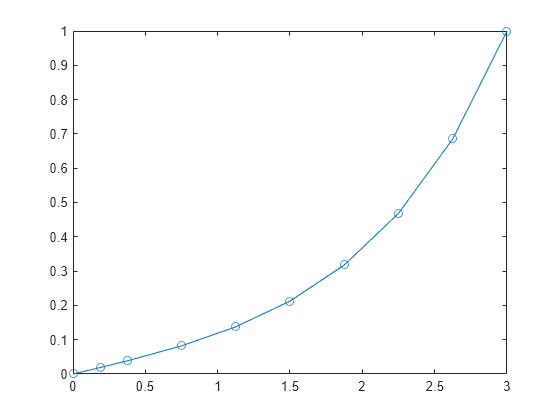

区間の拡張

次に、bvpinit を使用してループで積分区間を拡張し、新しい問題をそれぞれ解いてプロットします。反復ごとに、新しい区間 [0 k] に外挿された前の解 sol を使用して、初期推定を作成します。新しい問題のそれぞれで、bvp4c は境界条件を新しい境界 [0 k] に適用します。

hold on
for k = 4:8
    solinit = bvpinit(sol,[0 k]);
    sol = bvp4c(@bvpfun, @bcfun, solinit);
    plot(sol.x(1,:),sol.y(1,:),'-o')
end

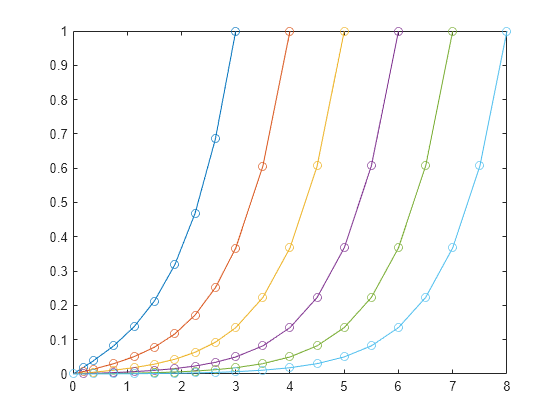
この例は、簡略化されたバージョンの "連続性" を示しています。これは、問題を小さな区間や単純な問題に分割して BVP を解く、便利な手法です。この手法の他の例については、次を参照してください。

• 連続性を使って BVP を解く

• 連続性を使用した BVP の整合性の検証

ローカル関数

ここでは、BVP ソルバー bvp4c が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function dydx = bvpfun(x,y) % equation being solved
dydx = [y(2)
        y(1)];
end
%-------------------------------------------
function res = bcfun(ya,yb) % boundary conditions
res = [ya(1)
       yb(1)-1];
end
%-------------------------------------------
function y = guess(x) % guess at solution behavior
y = [exp(x)
     exp(x)];
end
%-------------------------------------------

入力引数

x — 初期メッシュ

ベクトル

初期メッシュ。ベクトルとして指定します。この問題を区間 [a,b] で解くには、x(1) を a、x(end) を b として指定します。x のエントリは、昇順 (a < b の場合) または降順 (a > b の場合) でなければなりません。ソルバーはこのメッシュを解に合わせて (メッシュ点の追加、削除および移動により) 適切に変更するので、多くの場合、x = linspace(a,b,10) のような推定で十分です。難しい問題を処理するには、いくつかのメッシュ点を、解が急速に変化する位置に配置します。

• "2 点" 境界値問題の場合、x のエントリは一意でなければなりません。すなわち、a < b である場合、エントリは x(1) < x(2) < ... < x(end) を満たさなければなりません。a > b の場合、エントリは x(1) > x(2) > ... > x(end) を満たさなければなりません。

• "多点" 境界値問題の場合は、端点 a および b の他に、x 内でエントリを繰り返すことにより、境界条件が適用される [a,b] 内の点を指定できます。たとえば、次のベクトルについて考えます。

  x = [0 0.5 1 1 1.5 2];

  このメッシュでは、境界条件は端点 0 と 2、および繰り返されたエントリ 1 の 3 点に適用されます。一般に、繰り返されたエントリは、[a,b] 内における領域の境界点を表します。繰り返されたエントリ 1 は、区間 [0 2] を [0 1] と [1 2] の 2 つの領域に分割します。

例: solinit = bvpinit(linspace(a,b,10),yinit)

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
複素数のサポート: あり

yinit — 解の初期推定

ベクトル | 関数

解の初期推定。ベクトルまたは関数として指定します。

• ベクトル – 解の個々の成分について bvpinit は、すべてのメッシュ点における一定の推定として、ベクトルの対応する要素を複製します。すなわち、yinit(i) は、x のすべてのメッシュ点における解の i 番目の成分 yinit(i,:) に関する定数の推定です。

• 関数 – 推定関数は、指定されたメッシュ点について、解の対応する成分に関する推定を要素とするベクトルを返さなければなりません。関数は、次の形式になります。

  y = guess(x)

  x はメッシュ点、y は解の成分数と同じ長さをもつベクトルです。たとえば、yinit が関数の場合、bvpinit は各メッシュ点で次を呼び出します。

  y(:,j) = guess(x(j))

  多点境界値問題の場合、推定関数は、以下の形式でなければなりません。

  y = guess(x,k)

  y は、領域 k の x における解の初期推定です。この関数は入力引数 k を受け入れる必要があり、これは推定関数を柔軟に記述できるようにするための仕様です。とはいえ、関数内で必ず k を使用する必要はありません。

例: solinit = bvpinit(x,[sqrt(3)/2; 0])

例: solinit = bvpinit(x,@guess)

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | function_handle
複素数のサポート: あり

parameters — 未知パラメーター値の初期推定

スカラー | ベクトル

未知パラメーター値の初期推定。スカラーまたはベクトルとして指定します。

例: solinit = bvpinit(x, yinit, [0 1 sqrt(2)]) は 3 つの未知パラメーターの推定ベクトルを指定します。

例: 未知パラメーターをもつ BVP の例を表示するには、edit mat4bvp と入力します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
複素数のサポート: あり

sol — 前回の解

構造体

前回の解。bvp4c または bvp5c により返される解の構造体として指定します。sol がパラメーターを含む場合、そのパラメーターは solinit にコピーされます。

データ型: struct

出力引数

solinit — 解の初期推定

構造体

解の初期推定。構造体として返されます。この構造体は、境界値問題を解くための bvp4c または bvp5c の 3 番目の入力として使用します。

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

バージョン履歴

R2006a より前に導入

参考

bvp4c | bvp5c | bvpget | bvpset | bvpxtend | deval