連続性を使用した BVP の整合性の検証

この例では、連続性を使用して BVP 解を徐々に拡大し、より大きな区間にする方法について説明します。

Falkner-Skan 境界値問題 [1] は、平坦な平面上での粘性、非圧縮の層流の近似解に起因しています。方程式例は次のようになります。

${{{\mathit{f}}^{\prime }}^{\prime }}^{\prime }+\mathit{f}{{\mathit{f}}^{\prime }}^{\prime }+\beta \left(1-{{\mathit{f}}^{\prime }}^2\right)=0$.

問題は $\beta =0.5$ として無限区間 $\left[0,\infty \right]$ で提示されており、次の境界条件に従います。

$\mathit{f}\left(0\right)=0$,

${\mathit{f}}^{\prime }\left(0\right)=0$,

${\mathit{f}}^{\prime }\left(\infty \right)=1$.

BVP は無限区間では解くことができません。非常に大きな有限区間で BVP を解くことも現実的ではありません。代わりに、この例ではより小さい区間 $\left[0,\mathit{a}\right]$ で提示される一連の問題を解き、$\mathit{a}\to \infty$ とともに解が整合性のある動作を示すことを確認します。問題をより単純な問題に分割し、各問題の解を次の問題の初期推定としてフィード バックするこの手法は、"連続性" と呼ばれています。

MATLAB® でこの方程式系を解くには、方程式、境界条件、およびオプションをコード化してから、境界値問題ソルバー bvp4c を呼び出す必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

方程式のコード化

方程式をコード化する関数を作成します。この関数にはシグネチャ dfdx = fsode(x,f) がなければなりません。ここでは以下のようになります。

• x は独立変数です。

• f は従属変数です。

${\mathit{f}}_1=\mathit{f}$、${\mathit{f}}_2={\mathit{f}}^{\prime }$、および ${\mathit{f}}_3={{\mathit{f}}^{\prime }}^{\prime }$ の代入を使用して、3 次方程式を 1 次方程式系に書き換えることができます。方程式は次のようになります。

${{\mathit{f}}_1}^{\prime }={\mathit{f}}_2$,

${{\mathit{f}}_2}^{\prime }={\mathit{f}}_3$,

${{\mathit{f}}_3}^{\prime }=-{\mathit{f}}_1{\mathit{f}}_3-\beta \left(1-{\mathit{f}}_2^2\right)$.

対応する関数は次のようになります。

function dfdeta = fsode(x,f)
b = 0.5;
dfdeta = [ f(2)
           f(3)
          -f(1)*f(3) - b*(1 - f(2)^2) ];
end

メモ: 関数はすべて例の最後にローカル関数として含まれます。

境界条件のコード化

次に、境界点で境界条件の残差値を返す関数を記述します。この関数にはシグネチャ res = fsbc(f0,finf) がなければなりません。ここでは以下のようになります。

• f0 は、区間の始まりにある境界条件の値です。

• finf は、区間の終わりにある境界条件の値です。

残差値を計算するには、境界条件を $\mathit{g}\left(\mathit{x},\mathit{y}\right)=0$ の形式にする必要があります。この形式では、境界条件は次のようになります。

$\mathit{f}\left(0\right)=0$,

${\mathit{f}}^{\prime }\left(0\right)=0$,

${\mathit{f}}^{\prime }\left(\infty \right)-1=0$.

対応する関数は次のようになります。

function res = fsbc(f0,finf)
res = [f0(1)
       f0(2)
       finf(2) - 1];
end

初期推定の作成

最後に、解の初期推定を提供しなければなりません。5 つの点の粗いメッシュと境界条件を満たす定数の推定値を使えば、区間 $\left[0,3\right]$ で収束を得ることができます。変数 infinity は、積分区間の右側の制限を示しています。後続の反復で infinity の値が 3 から最大値の 6 まで増加するときに、前の各反復の解が次の反復の初期推定として機能します。

infinity = 3;
maxinfinity = 6;
solinit = bvpinit(linspace(0,infinity,5),[0 0 1]);

方程式を解いて解をプロット

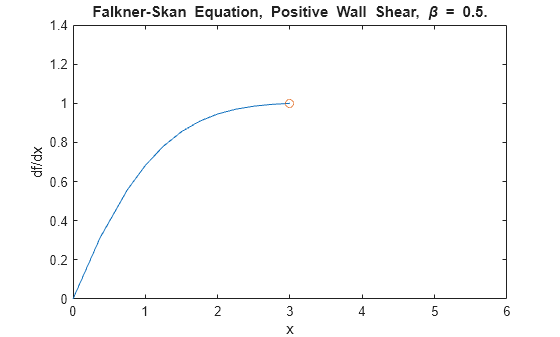
初期区間 $\left[0,3\right]$ で問題を解きます。解をプロットし、${{\mathit{f}}^{\prime }}^{\prime }\left(0\right)$ の値を解析値 [1] と比較します。

sol = bvp4c(@fsode,@fsbc,solinit);
x = sol.x;
f = sol.y;
plot(x,f(2,:),x(end),f(2,end),'o');
axis([0 maxinfinity 0 1.4]);
title('Falkner-Skan Equation, Positive Wall Shear, \beta = 0.5.')
xlabel('x')
ylabel('df/dx')
hold on

fprintf('Cebeci & Keller report that f''''(0) = 0.92768.\n')

Cebeci & Keller report that f''(0) = 0.92768.

fprintf('Value computed using infinity = %g is %7.5f.\n', ...
         infinity,f(3,1))

Value computed using infinity = 3 is 0.92915.

ここで、反復ごとに infinity の値を増やすことで、区間を徐々に大きくしながら問題を解きます。関数 bvpinit は各解を新しい区間に外挿して、infinity の次の値の初期推定として機能させます。各反復では ${{\mathit{f}}^{\prime }}^{\prime }\left(0\right)$ の計算された値を表示し、解のプロットを前の解に重ね合わせます。infinity = 6 である場合、解の整合的な動作が明らかになり、${{\mathit{f}}^{\prime }}^{\prime }\left(0\right)$ の値は予測された値と非常に近くなります。

for Bnew = infinity+1:maxinfinity
  solinit = bvpinit(sol,[0 Bnew]); % Extend solution to new interval
  sol = bvp4c(@fsode,@fsbc,solinit);
  x = sol.x;
  f = sol.y;
  
  fprintf('Value computed using infinity = %g is %7.5f.\n', ...
           Bnew,f(3,1))
  plot(x,f(2,:),x(end),f(2,end),'o');
  drawnow
end

Value computed using infinity = 4 is 0.92774.
Value computed using infinity = 5 is 0.92770.
Value computed using infinity = 6 is 0.92770.

hold off

ローカル関数

ここでは、BVP ソルバー bvp4c が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function dfdeta = fsode(x,f) % equation being solved
dfdeta = [ f(2)
           f(3)
          -f(1)*f(3) - 0.5*(1 - f(2)^2) ];
end 
%-------------------------------------------
function res = fsbc(f0,finf) % boundary conditions
res = [f0(1)
       f0(2)
       finf(2) - 1];
end
%-------------------------------------------

参照

[1] Cebeci, T. and H. B. Keller."Shooting and Parallel Shooting Methods for Solving the Falkner-Skan Boundary-layer Equation."J. Comp.Phys., Vol. 7, 1971, pp. 289-300.

参考

bvp4c | bvp5c | bvpinit

関連するトピック

• 境界値問題の求解
• 連続性を使って BVP を解く