2 つの解をもつ BVP を解く

この例は 2 つの異なる初期推定をもつ bvp4c を使用して BVP の問題に対する両方の解を求めます。

次の微分方程式を考慮します。

${y^{'}}^{'} + e^{y} = 0$ .

この方程式が制約される境界条件は次のとおりです。

$y (0) = y (1) = 0$ .

MATLAB® でこの方程式を解くには、方程式と境界条件をコード化し、解に適した初期推定を生成してから、境界値問題ソルバー bvp4c を呼び出す必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

方程式のコード化

方程式をコード化する関数を作成します。この関数にはシグネチャ dydx = bvpfun(x,y) または dydx = bvpfun(x,y,parameters) がなければなりません。ここで次のようになります。

x は独立変数です。
y は解 (従属変数) です。
parameters は未知パラメーター値のベクトルです (オプション)。

これらの入力はソルバーによって自動的に関数に渡されますが、変数名によって方程式のコード化方法が決まります。この場合、2 次方程式を次の 1 次方程式系として書き換えできます。

${y_{1}}^{'} = y_{2}$ ,

${y_{2}}^{'} = - e^{y_{1}}$ .

これらの方程式をエンコードする関数は次のとおりです。

function dydx = bvpfun(x,y)
dydx = [y(2)
        -exp(y(1))];
end

境界条件のコード化

この問題のような 2 点境界値条件の場合、未知パラメーターが含まれるかどうかによって、境界条件関数にシグネチャ res = bcfun(ya,yb) または res = bcfun(ya,yb,parameters) がなければなりません。ya と yb はソルバーが自動的に関数に渡す列ベクトルであり、bcfun は境界条件に残差を返します。

境界条件 $y (0) = y (1) = 0$ の場合、関数 bcfun は両方の境界で残差値をゼロに指定します。これらの残差値は、初期推定で bvpinit に指定するメッシュの最初と最後の点で適用されます。この問題の初期メッシュには x(1) = 0 と x(end) = 1 がなければなりません。

function res = bcfun(ya,yb)
res = [ya(1)
       yb(1)];
end

初期推定の作成

bvpinit を呼び出して解の初期推定を生成します。x のメッシュに多数の点は必要ありませんが、最初の点は 0 でなければなりません。境界条件が正しく指定されるように、最後の点は 1 でなければなりません。最初の要素がわずかに正で、2 番目の要素がゼロである y の初期推定を使用します。

xmesh = linspace(0,1,5);
solinit = bvpinit(xmesh, [0.1 0]);

方程式の求解

bvp4c ソルバーを使用して BVP を解きます。

sol1 = bvp4c(@bvpfun, @bcfun, solinit);

異なる初期推定の使用

解に異なる初期推定を使用して 2 度目の BVP を解きます。

solinit = bvpinit(xmesh, [3 0]);
sol2 = bvp4c(@bvpfun, @bcfun, solinit);

解の比較

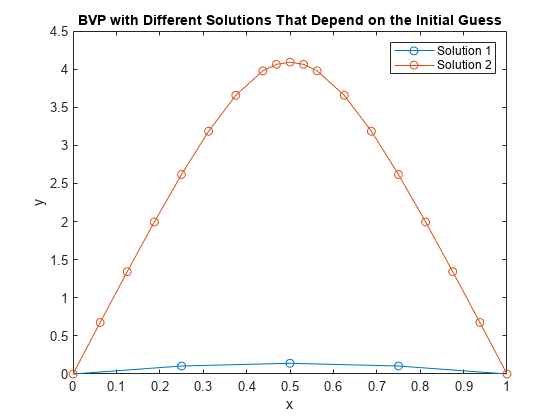
さまざまな初期条件を bvp4c が計算する解をプロットします。両方の解は指定された境界条件を満たしますが、動作は異なります。解が常に一意であるとは限らないため、さまざまな動作は解に適切な初期推定を指定する重要性を示します。

plot(sol1.x,sol1.y(1,:),'-o',sol2.x,sol2.y(1,:),'-o')
title('BVP with Different Solutions That Depend on the Initial Guess')
xlabel('x')
ylabel('y')
legend('Solution 1','Solution 2')

ローカル関数

ここでは、BVP ソルバー bvp4c が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function dydx = bvpfun(x,y) % equation being solved
dydx = [y(2)
        -exp(y(1))];
end
%-------------------------------------------
function res = bcfun(ya,yb) % boundary conditions 
res = [ya(1)
       yb(1)];
end
%-------------------------------------------

参考

bvp4c | bvp5c | bvpinit