1 次元偏微分方程式

放物型および楕円型偏微分方程式の 1 次元ソルバー

偏微分方程式には、複数の変数に依存する関数の偏微分が含まれています。MATLAB^® では、時間と 1 つの空間変数の関数について放物型偏微分方程式と楕円型偏微分方程式を解くことができます。詳細については、偏微分方程式の求解を参照してください。

Partial Differential Equation Toolbox™ は、ディリクレとノイマンの境界条件によって、この機能を 2 次元および 3 次元の問題へと拡張します。

関数

`pdepe`	1 次元の放物型および楕円型 PDE の求解
`odeget`	ODE のオプション値を抽出
`odeset`	ODE ソルバーおよび PDE ソルバーのオプション構造体を作成または変更
`pdeval`	PDE の数値解の内挿

偏微分方程式の求解
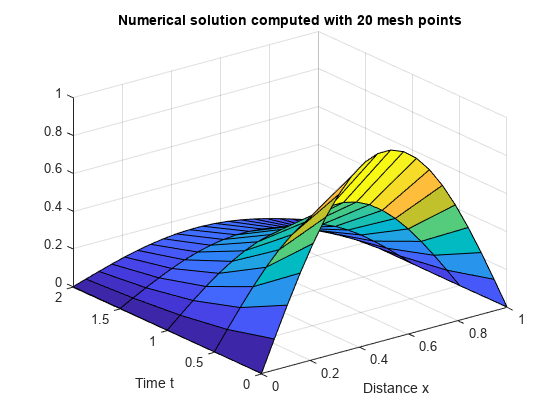
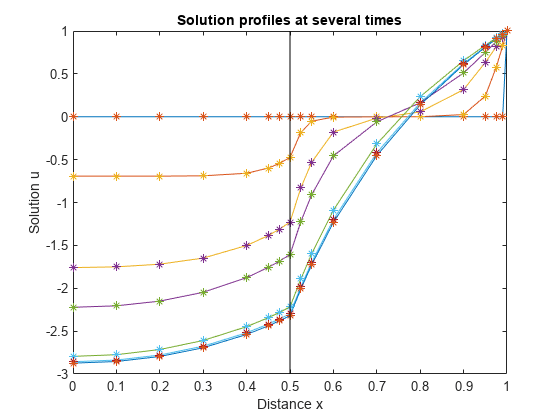
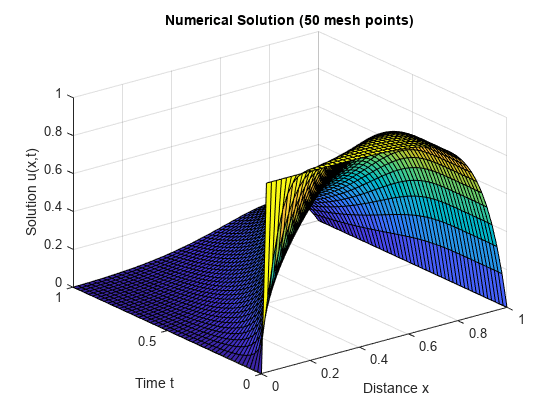
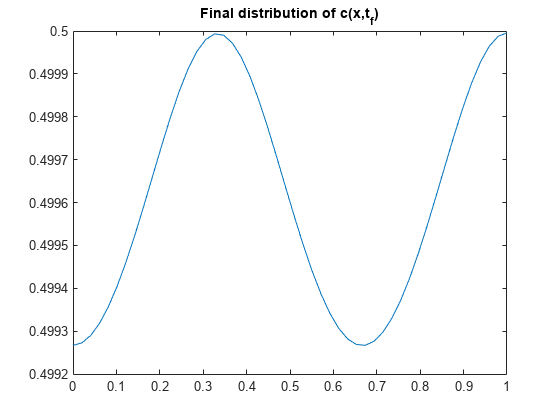
pdepe を使用して 1 次元偏微分方程式を解く。
単一の PDE の求解
この例では、単一の PDE の定式化、計算、および解のプロット方法を説明します。
不連続性をもつ PDE の求解
この例では、物質と境界を接する PDE を解く方法を説明します。
PDE の求解と偏導関数の計算
この例では、トランジスタの偏微分方程式 (PDE) を解き、その結果を使用して、より大きな問題を解くための一部をなす偏導関数を取得する方法を説明します。
PDE 系の求解
この例では、2 つの偏微分方程式系の定式化、計算、および解のプロットを行う方法を説明します。
初期条件のステップ関数をもつ PDE 系の求解
この例では、初期条件でステップ関数を使用する偏微分方程式系を解く方法を説明します。