不連続性をもつ PDE の求解

この例では、物質と境界を接する PDE を解く方法を説明します。この問題では $x = 0.5$ において物質の境界により不連続性が作成され、初期条件には右の境界 $x = 1$ に不連続性があります。

区分的な PDE を考えます。

${\begin{matrix} \frac{\partial u}{\partial t} = x^{- 2} \frac{\partial}{\partial x} (x^{2} 5 \frac{\partial u}{\partial x}) - 1000 e^{u} & (0 \leq x \leq 0.5) \\ \frac{\partial u}{\partial t} = x^{- 2} \frac{\partial}{\partial x} (x^{2} \frac{\partial u}{\partial x}) - e^{u} & (0.5 \leq x \leq 1) \end{matrix}$

初期条件は次のとおりです。

$\begin{array}{l} u (x, 0) = 0 (0 \leq x < 1), \\ u (1, 0) = 1 (x = 1) . \end{array}$

境界条件は次のとおりです。

$\begin{array}{l} \frac{\partial u}{\partial x} = 0 (x = 0), \\ u (1, t) = 1 (x = 1) . \end{array}$

この方程式を MATLAB® で解くには、方程式、初期条件、および境界条件をコード化し、適切な解のメッシュを選択してから、ソルバー pdepe を呼び出す必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

方程式のコード化

方程式をコード化する前に、それが pdepe ソルバーで想定される形式であることを確認する必要があります。pdepe で想定される標準形式は次のとおりです。

$c (x, t, u, \frac{\partial u}{\partial x}) \frac{\partial u}{\partial t} = x^{- m} \frac{\partial}{\partial x} (x^{m} f (x, t, u, \frac{\partial u}{\partial x})) + s (x, t, u, \frac{\partial u}{\partial x})$ .

この場合、PDE は適切な形式であるため、係数の値を読み取ることができます。

流束項 $f (x, t, u, \frac{\partial u}{\partial x})$ とソース項 $s (x . t, u, \frac{\partial u}{\partial x})$ の値は、 $x$ の値に応じて変化します。係数は次のようになります。

$m = 2$

$c (x, t, u, \frac{\partial u}{\partial x}) = 1$

${\begin{matrix} f (x, t, u, \frac{\partial u}{\partial x}) = 5 \frac{\partial u}{\partial x} & (0 \leq x \leq 0.5) \\ f (x, t, u, \frac{\partial u}{\partial x}) = \frac{\partial u}{\partial x} & (0.5 \leq x \leq 1) \end{matrix}$

${\begin{matrix} s (x, t, u, \frac{\partial u}{\partial x}) = - 1000 e^{u} & (0 \leq x \leq 0.5) \\ s (x, t, u, \frac{\partial u}{\partial x}) = - e^{u} & (0.5 \leq x \leq 1) \end{matrix}$

これで、方程式をコード化する関数を作成できるようになりました。この関数にはシグネチャ [c,f,s] = pdex2pde(x,t,u,dudx) がなければなりません。

x は独立空間変数。
t は独立時間変数。
u は、x および t について微分される従属変数。
dudx は空間偏導関数 $\partial u / \partial x$ 。
出力 c、f、および s は、pdepe で想定される標準 PDE 方程式形式の係数に対応。これらの係数は、入力変数 x、t、u、および dudx によってコード化されます。

結果として、この例の方程式は次の関数で表すことができます。

function [c,f,s] = pdex2pde(x,t,u,dudx)
c = 1;
if x <= 0.5
    f = 5*dudx;
    s = -1000*exp(u);
else
    f = dudx;
    s = -exp(u);
end
end

(メモ: 関数はすべて例の最後にローカル関数として含まれます。)

初期条件のコード化

次に、初期条件を返す関数を記述します。初期条件は最初の時間値において適用され、 $u (x, t_{0})$ の値を任意の $x$ の値に対して提供します。関数シグネチャ u0 = pdex2ic(x) を使用して関数を記述します。

初期条件は次のとおりです。

$\begin{array}{l} u (x, 0) = 0 (0 \leq x < 1), \\ u (1, 0) = 1 (x = 1) . \end{array}$

対応する関数は次のようになります。

function u0 = pdex2ic(x)
if x < 1
    u0 = 0;
else
    u0 = 1;
end
end

境界条件のコード化

次に、境界条件を評価する関数を記述します。区間 $a \leq x \leq b$ で提示される問題について、境界条件はすべての t、および $x = a$ または $x = b$ のいずれかに適用されます。ソルバーで想定される境界条件の標準形式は次のとおりです。

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

この例には球面対称性 ( $m = 2$ ) があるため、pdepe ソルバーは左境界条件を自動的に強制して解を原点に拘束し、境界関数内で左境界に指定された条件はすべて無視します。したがって、左境界条件には $p_{L} = q_{L} = 0$ を指定できます。右境界条件については、境界条件を標準形式で書き直し、 $p_{R}$ と $q_{R}$ の係数値を読み取ることができます。

$x = 1$ に対し、方程式は $u (1, t) = 1 \to (u - 1) + 0 \cdot \frac{\partial u}{\partial x} = 0$ になります。係数は次のようになります。

$p_{R} (1, t, u) = u - 1$
$q_{R} (1, t) = 0$

境界関数は関数シグネチャ [pl,ql,pr,qr] = pdex2bc(xl,ul,xr,ur,t) を使用しなければなりません。

入力 xl および ul は左境界の u および x に対応。
入力 xr および ur は右境界の u および x に対応。
t は独立時間変数。
出力 pl および ql は左境界 (この問題では $x = 0$ ) の $p_{L} (x, t, u)$ および $q_{L} (x, t)$ に対応。
出力 pr および qr は右境界 (この問題では $x = 1$ ) の $p_{R} (x, t, u)$ および $q_{R} (x, t)$ に対応。

この例の境界条件は次の関数で表されます。

function [pl,ql,pr,qr] = pdex2bc(xl,ul,xr,ur,t)
pl = 0; 
ql = 0; 
pr = ur - 1;
qr = 0;
end

解のメッシュの選択

空間メッシュは、不連続な境界を考慮するために $x = 0.5$ 近傍の値をいくつか含んでいなければならず、また、 $x = 1$ 近傍の点を含んでいなければなりません。これは、その点での初期値 ( $u (1, 0) = 1$ ) と境界値 ( $u (1, t) = 0$ ) が一致しないためです。小さい $t$ に対して解は急速に変化するため、この急激な変化を解決できるタイムステップを使用します。

x = [0 0.1 0.2 0.3 0.4 0.45 0.475 0.5 0.525 0.55 0.6 0.7 0.8 0.9 0.95 0.975 0.99 1];
t = [0 0.001 0.005 0.01 0.05 0.1 0.5 1];

方程式の求解

最後に、対称性 m、PDE 方程式、初期条件、境界条件、および x と t のメッシュを使用して方程式を解きます。

m = 2;
sol = pdepe(m,@pdex2pde,@pdex2ic,@pdex2bc,x,t);

pdepe は 3 次元配列 sol に解を返します。ここで、sol(i,j,k) は t(i) と x(j) で評価した解の k 番目の要素 $u_{k}$ を近似します。u0 が各解要素の初期条件を指定するため、sol のサイズは length(t) x length(x) x length(u0) となります。この問題では、u の要素は 1 つのみであるため、sol は 8 行 18 列の行列になりますが、通常はコマンド u = sol(:,:,k) を使用して k 番目の解要素を抽出できます。

最初の解要素を sol から抽出します。

u = sol(:,:,1);

解のプロット

$x$ と $t$ の選択されたメッシュ点でプロットされた解 $u$ の表面プロットを作成します。 $m = 2$ であるため、問題は球面対称性をもつ球面幾何学で提示されます。したがって、解は半径 $x$ の方向にのみ変化します。

surf(x,t,u)
title('Numerical solution with nonuniform mesh')
xlabel('Distance x')
ylabel('Time t')
zlabel('Solution u')

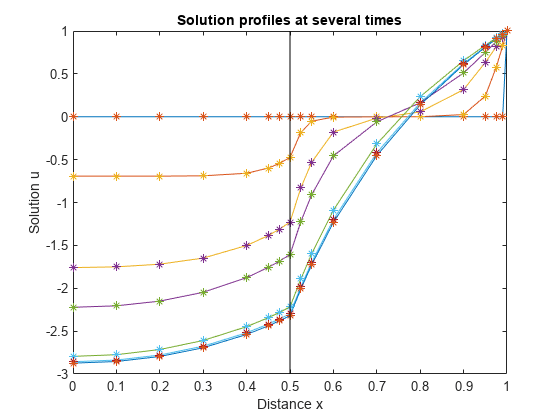
次に、 $x$ と $u$ のみをプロットして、表面プロットの等高線の側面図を取得します。 $x = 0.5$ にラインを追加して、物質の境界の影響を強調表示します。

plot(x,u,x,u,'*')
line([0.5 0.5], [-3 1], 'Color', 'k')
xlabel('Distance x')
ylabel('Solution u')
title('Solution profiles at several times')

ローカル関数

ここでは、PDE ソルバー pdepe が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function [c,f,s] = pdex2pde(x,t,u,dudx) % Equation to solve
c = 1;
if x <= 0.5
    f = 5*dudx;
    s = -1000*exp(u);
else
    f = dudx;
    s = -exp(u);
end
end
%----------------------------------------------
function u0 = pdex2ic(x) %Initial conditions
if x < 1
    u0 = 0;
else
    u0 = 1;
end
end
%----------------------------------------------
function [pl,ql,pr,qr] = pdex2bc(xl,ul,xr,ur,t) % Boundary conditions
pl = 0;
ql = 0;
pr = ur - 1;
qr = 0;
end
%----------------------------------------------

参考

pdepe