PDE の求解と偏導関数の計算

この例では、トランジスタの偏微分方程式 (PDE) を解き、その結果を使用して、より大きな問題を解くための一部をなす偏導関数を取得する方法を説明します。

次の PDE を考えます。

$$\frac{\partial \mathit{u}}{\partial \mathit{t}}=\mathit{D}\frac{{\partial }^2\mathit{u}}{\partial {\mathit{x}}^2}-\frac{\mathit{D}\eta }{\mathit{L}}\frac{\partial \mathit{u}}{\partial \mathit{x}}.$$

この方程式はトランジスタの理論 [1] で使われ、$\mathit{u}\left(\mathit{x},\mathit{t}\right)$ は PNP トランジスタのベースにおける過剰電荷キャリア ("ホール") の濃度を記述する関数です。$\mathit{D}$ と $\eta$ は物理定数です。この方程式は、時間 $\mathit{t}\ge 0$ に対して区間 $0\le \mathit{x}\le \mathit{L}$ で成立します。

初期条件には定数 $\mathit{K}$ が含まれ、次によって与えられます。

$$\mathit{u}\left(\mathit{x},0\right)=\frac{\mathit{K}\mathit{L}}{\mathit{D}}\left(\frac{1-{\mathit{e}}^{-\eta \left(1-\mathit{x}/\mathit{L}\right)}}{\eta }\right).$$

この問題の境界条件は次によって与えられます。

$$\mathit{u}\left(0,\mathit{t}\right)=\mathit{u}\left(\mathit{L},\mathit{t}\right)=0.$$

$\mathit{x}$ が固定の場合、方程式 $\mathit{u}\left(\mathit{x},\mathit{t}\right)$ の解は $\mathit{t}\to \infty$ に伴う過剰電荷の急減少を記述します。この急減少により、"エミッター放電電流" という電流が発生しますが、この電流には別の定数 ${\mathit{I}}_{\mathit{p}}$ があります。

$$\mathit{I}\left(\mathit{t}\right)={\left[\frac{{\mathit{I}}_{\mathit{p}}\mathit{D}}{\mathit{K}}\frac{\partial }{\partial \mathit{x}}\mathit{u}\left(\mathit{x},\mathit{t}\right)\right]}_{\mathit{x}=0}.$$

$\mathit{t}=0$ および $\mathit{t}>0$ の場合に $\mathit{x}=0$ での境界値が一定でないため、この方程式は $\mathit{t}>0$ の場合に有効です。PDE には、$\mathit{u}\left(\mathit{x},\mathit{t}\right)$ の閉形式の級数解があるため、エミッター放電電流を解析的および数値的に計算して、結果を比較できます。

MATLAB® でこの問題を解くには、PDE 方程式、初期条件、および境界条件をコード化し、適切な解のメッシュを選択してから、ソルバー pdepe を呼び出す必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

物理定数の定義

物理定数を追跡するために、各定数のフィールドをもつ構造体配列を作成します。後で方程式、初期条件、および境界条件に用いる関数を定義するときに、この構造体を追加の引数として渡して、関数で定数にアクセスできるようにします。

C.L = 1;
C.D = 0.1;
C.eta = 10;
C.K = 1;
C.Ip = 1;

方程式のコード化

方程式をコード化する前に、それが pdepe ソルバーで想定される形式であることを確認する必要があります。

$$\mathit{c}\left(\mathit{x},\mathit{t},\mathit{u},\frac{\partial \mathit{u}}{\partial \mathit{x}}\right)\frac{\partial \mathit{u}}{\partial \mathit{t}}={\mathit{x}}^{-\mathit{m}}\frac{\partial }{\partial \mathit{x}}\left({\mathit{x}}^{\mathit{m}}\mathit{f}\left(\mathit{x},\mathit{t},\mathit{u},\frac{\partial \mathit{u}}{\partial \mathit{x}}\right)\right)+\mathit{s}\left(\mathit{x},\mathit{t},\mathit{u},\frac{\partial \mathit{u}}{\partial \mathit{x}}\right).$$

この形式では、PDE は次のようになります。

$$\frac{\partial \mathit{u}}{\partial \mathit{t}}={\mathit{x}}^0\frac{\partial }{\partial \mathit{x}}\left({\mathit{x}}^0\mathit{D}\frac{\partial \mathit{u}}{\partial \mathit{x}}\right)-\frac{\mathit{D}\eta }{\mathit{L}}\frac{\partial \mathit{u}}{\partial \mathit{x}}.$$

したがって、方程式の係数の値は次のようになります。

• $$\mathit{m}=0$$ (角対称性のない直交座標)

• $$\mathit{c}\left(\mathit{x},\mathit{t},\mathit{u},\frac{\partial \mathit{u}}{\partial \mathit{x}}\right)=1$$

• $$\mathit{f}\left(\mathit{x},\mathit{t},\mathit{u},\frac{\partial \mathit{u}}{\partial \mathit{x}}\right)=\mathit{D}\frac{\partial \mathit{u}}{\partial \mathit{x}}$$

• $$\mathit{s}\left(\mathit{x},\mathit{t},\mathit{u},\frac{\partial \mathit{u}}{\partial \mathit{x}}\right)=-\frac{\mathit{D}\eta }{\mathit{L}}\frac{\partial \mathit{u}}{\partial \mathit{x}}$$

これで、方程式をコード化する関数を作成できるようになりました。この関数にはシグネチャ [c,f,s] = transistorPDE(x,t,u,dudx,C) がなければなりません。

• x は独立空間変数。

• t は独立時間変数。

• u は、x および t について微分される従属変数。

• dudx は空間偏導関数 $\partial \mathit{u}/\partial \mathit{x}$。

• C は物理定数を含む追加の入力。

• 出力 c、f、および s は、pdepe で想定される標準 PDE 方程式形式の係数に対応。

結果として、この例の方程式は次の関数で表すことができます。

function [c,f,s] = transistorPDE(x,t,u,dudx,C)
D = C.D;
eta = C.eta;
L = C.L;

c = 1;
f = D*dudx;
s = -(D*eta/L)*dudx;
end

(メモ: 関数はすべて例の最後にローカル関数として含まれます。)

初期条件のコード化

次に、初期条件を返す関数を記述します。初期条件は最初の時間値において適用され、$\mathit{u}\left(\mathit{x},{\mathit{t}}_0\right)$ の値を任意の $\mathit{x}$ の値に対して提供します。関数シグネチャ u0 = transistorIC(x,C) を使用して関数を記述します。

初期条件は次のとおりです。

$\mathit{u}\left(\mathit{x},0\right)=\frac{\mathit{K}\mathit{L}}{\mathit{D}}\left(\frac{1-{\mathit{e}}^{-\eta \left(1-\mathit{x}/\mathit{L}\right)}}{\eta }\right).$

対応する関数は次のようになります。

function u0 = transistorIC(x,C)
K = C.K;
L = C.L;
D = C.D;
eta = C.eta;

u0 = (K*L/D)*(1 - exp(-eta*(1 - x/L)))/eta;
end

境界条件のコード化

次に、境界条件 $\mathit{u}\left(0,\mathit{t}\right)=\mathit{u}\left(1,\mathit{t}\right)=0$ を評価する関数を記述します。区間 $\mathit{a}\le \mathit{x}\le \mathit{b}$ で提示される問題について、境界条件はすべての $\mathit{t}$、および $\mathit{x}=\mathit{a}$ または $\mathit{x}=\mathit{b}$ のいずれかに適用されます。ソルバーで想定される境界条件の標準形式は次のとおりです。

$$\mathit{p}\left(\mathit{x},\mathit{t},\mathit{u}\right)+\mathit{q}\left(\mathit{x},\mathit{t}\right)\mathit{f}\left(\mathit{x},\mathit{t},\mathit{u},\frac{\partial \mathit{u}}{\partial \mathit{x}}\right)=0.$$

この形式で記述すると、この問題の境界条件は次のようになります。

- $\mathit{x}=0$ の場合、方程式は $\mathit{u}+0\cdot \mathit{d}\frac{\partial \mathit{u}}{\partial \mathit{x}}=0.$ となります。係数は次のとおりです。

• $${\mathit{p}}_{\mathit{L}}\left(\mathit{x},\mathit{t},\mathit{u}\right)=\mathit{u},$$

• $${\mathit{q}}_{\mathit{L}}\left(\mathit{x},\mathit{t}\right)=0.$$

- 同様に $\mathit{x}=1$ の場合、方程式は $\mathit{u}+0\cdot \mathit{d}\frac{\partial \mathit{u}}{\partial \mathit{x}}=0.$ となります。係数は次のとおりです。

• $${\mathit{p}}_{\mathit{R}}\left(\mathit{x},\mathit{t},\mathit{u}\right)=\mathit{u},$$

• $${\mathit{q}}_{\mathit{R}}\left(\mathit{x},\mathit{t}\right)=0.$$

境界関数は関数シグネチャ [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t) を使用しなければなりません。

• 入力 xl および ul は左境界の $\mathit{x}$ および $\mathit{u}$ に対応。

• 入力 xr および ur は右境界の $\mathit{x}$ および $\mathit{u}$ に対応。

• t は独立時間変数。

• 出力 pl および ql は左境界 (この問題では $\mathit{x}=0$) の ${\mathit{p}}_{\mathit{L}}\left(\mathit{x},\mathit{t},\mathit{u}\right)$ および ${\mathit{q}}_{\mathit{L}}\left(\mathit{x},\mathit{t}\right)$ に対応。

• 出力 pr および qr は右境界 (この問題では $\mathit{x}=1$) の ${\mathit{p}}_{\mathit{R}}\left(\mathit{x},\mathit{t},\mathit{u}\right)$ および ${\mathit{q}}_{\mathit{R}}\left(\mathit{x},\mathit{t}\right)$ に対応。

この例の境界条件は次の関数で表されます。

function [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t)
pl = ul;
ql = 0;
pr = ur;
qr = 0;
end

解のメッシュの選択

解のメッシュは、ソルバーで解が評価される位置である $\mathit{x}$ と $\mathit{t}$ の値を定義します。この問題の解は急速に変化するため、区間 $0\le \mathit{x}\le \mathit{L}$ で 50 個の空間点、区間 $0\le \mathit{t}\le 1$ で 50 個の時間点をもつ比較的細かいメッシュを使用します。

x = linspace(0,C.L,50);
t = linspace(0,1,50);

方程式の求解

最後に、対称性 $\mathit{m}$、PDE 方程式、初期条件、境界条件、および $\mathit{x}$ と $\mathit{t}$ のメッシュを使用して方程式を解きます。pdepe では、PDE 関数が 4 つの入力を使用し、初期条件関数が 1 つの入力を使用することが想定されているため、追加の入力として物理定数の構造体を渡す関数ハンドルを作成します。

m = 0;
eqn = @(x,t,u,dudx) transistorPDE(x,t,u,dudx,C);
ic = @(x) transistorIC(x,C);
sol = pdepe(m,eqn,ic,@transistorBC,x,t);

pdepe は 3 次元配列 sol に解を返します。ここで、sol(i,j,k) は t(i) と x(j) で評価した解の k 番目の要素 ${\mathit{u}}_{\mathit{k}}$ を近似します。この問題では u の要素は 1 つのみですが、通常はコマンド u = sol(:,:,k) を使って k 番目の解要素を抽出できます。

u = sol(:,:,1);

解のプロット

$\mathit{x}$ と $\mathit{t}$ の選択されたメッシュ点でプロットされた解 $\mathit{u}$ の表面プロットを作成します。

surf(x,t,u)
title('Numerical Solution (50 mesh points)')
xlabel('Distance x')
ylabel('Time t')
zlabel('Solution u(x,t)')

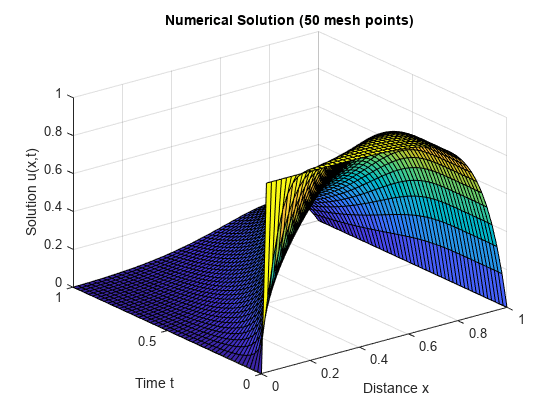
次に、$\mathit{x}$ と $\mathit{u}$ のみをプロットして、表面プロットの等高線の側面図を取得します。

plot(x,u)
xlabel('Distance x')
ylabel('Solution u(x,t)')
title('Solution profiles at several times')

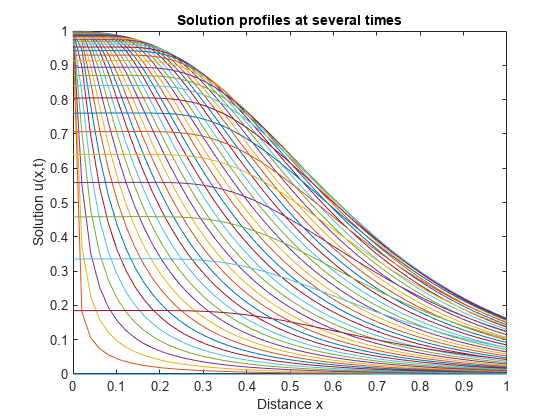
エミッター放電電流の計算

$\mathit{u}\left(\mathit{x},\mathit{t}\right)$ の級数解を使用して、エミッター放電電流を無限級数として表現できます [1]。

$$\mathit{I}\left(\mathit{t}\right)=2{\pi }^2{\mathit{I}}_{\mathit{p}}\left(\frac{1-{\mathit{e}}^{-\eta }}{\eta }\right)\sum _{\mathit{n}=1}^{\infty }\frac{{\mathit{n}}^2}{{\mathit{n}}^2{\pi }^2+{\eta }^2/4}{\mathit{e}}^{-\frac{\mathit{dt}}{{\mathit{L}}^2}\left({\mathit{n}}^2{\pi }^2+{\eta }^2/4\right)}.$$

この級数の 40 項を使用して $\mathit{I}\left(\mathit{t}\right)$ の解析解を計算する関数を記述します。変数は時間のみですが、定数の構造体を関数の 2 番目の入力に指定します。

function It = serex3(t,C) % Approximate I(t) by series expansion.
Ip = C.Ip;
eta = C.eta;
D = C.D;
L = C.L;

It = 0;
for n = 1:40 % Use 40 terms
  m = (n*pi)^2 + 0.25*eta^2;
  It = It + ((n*pi)^2 / m)* exp(-(D/L^2)*m*t);
end
It = 2*Ip*((1 - exp(-eta))/eta)*It;
end

pdepe で計算された $\mathit{u}\left(\mathit{x},\mathit{t}\right)$ の数値解を使用して、$\mathit{x}=0$ での $\mathit{I}\left(\mathit{t}\right)$ の数値近似を次により計算することもできます。

$$\mathit{I}\left(\mathit{t}\right)={\left[\frac{{\mathit{I}}_{\mathit{p}}\mathit{D}}{\mathit{K}}\frac{\partial }{\partial \mathit{x}}\mathit{u}\left(\mathit{x},\mathit{t}\right)\right]}_{\mathit{x}=0}.$$

$\mathit{I}\left(\mathit{t}\right)$ の解析解と数値解を計算し、結果をプロットします。pdeval を使用して、$\mathit{x}=0$ での $\partial \mathit{u}/\partial \mathit{x}$ の値を計算します。

nt = length(t);
I = zeros(1,nt);
seriesI = zeros(1,nt);
iok = 2:nt;
for j = iok
   % At time t(j), compute du/dx at x = 0.
   [~,I(j)] = pdeval(m,x,u(j,:),0);
   seriesI(j) = serex3(t(j),C);
end
% Numeric solution has form I(t) = (I_p*D/K)*du(0,t)/dx
I = (C.Ip*C.D/C.K)*I;

plot(t(iok),I(iok),'o',t(iok),seriesI(iok))
legend('From PDEPE + PDEVAL','From series')
title('Emitter discharge current I(t)')
xlabel('Time t')

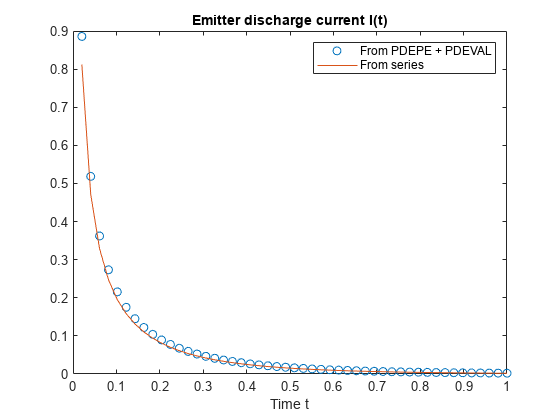
結果はかなり良く一致しています。より細かい解のメッシュを使用して、pdepe の数値結果をさらに改善することができます。

ローカル関数

ここでは、PDE ソルバー pdepe が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function [c,f,s] = transistorPDE(x,t,u,dudx,C) % Equation to solve
D = C.D;
eta = C.eta;
L = C.L;

c = 1;
f = D*dudx;
s = -(D*eta/L)*dudx;
end
% ----------------------------------------------------
function u0 = transistorIC(x,C) % Initial condition
K = C.K;
L = C.L;
D = C.D;
eta = C.eta;

u0 = (K*L/D)*(1 - exp(-eta*(1 - x/L)))/eta;
end
% ----------------------------------------------------
function [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t) % Boundary conditions
pl = ul;
ql = 0;
pr = ur;
qr = 0;
end
% ----------------------------------------------------
function It = serex3(t,C) % Approximate I(t) by series expansion.
Ip = C.Ip;
eta = C.eta;
D = C.D;
L = C.L;

It = 0;
for n = 1:40 % Use 40 terms
  m = (n*pi)^2 + 0.25*eta^2;
  It = It + ((n*pi)^2 / m)* exp(-(D/L^2)*m*t);
end
It = 2*Ip*((1 - exp(-eta))/eta)*It;
end
% ----------------------------------------------------

参照

[1] Zachmanoglou, E.C. and D.L. Thoe. Introduction to Partial Differential Equations with Applications. Dover, New York, 1986.

参考

pdepe

トピック

• 偏微分方程式の求解
• PDE 系の求解