PDE 系の求解

R2026a

ライブスクリプトを開く

この例では、2 つの方程式からなる連立偏微分方程式の定式化、計算、および解のプロットを行う方法を説明します。

次の PDE 系を考えます。

$\frac{\partial u_{1}}{\partial t} = 0.024 \frac{\partial^{2} u_{1}}{\partial x^{2}} - F (u_{1} - u_{2}),$

$\frac{\partial u_{2}}{\partial t} = 0.170 \frac{\partial^{2} u_{2}}{\partial x^{2}} + F (u_{1} - u_{2}) .$

(関数 $F (y) = e^{5.73 y} - e^{- 11.46 y}$ は省略表現として使用されます。)

この方程式は、時間 $t \geq 0$ に対して区間 $0 \leq x \leq 1$ で成立します。初期条件は次のとおりです。

$u_{1} (x, 0) = 1,$

$u_{2} (x, 0) = 0 .$

境界条件は次のとおりです。

$\begin{array}{l} \frac{\partial}{\partial x} u_{1} (0, t) = 0, \\ u_{2} (0, t) = 0, \\ \frac{\partial}{\partial x} u_{2} (1, t) = 0, \\ u_{1} (1, t) = 1 . \end{array}$

この方程式を MATLAB® で解くには、方程式、初期条件、および境界条件をコード化し、適切な解のメッシュを選択してから、ソルバー pdepe を呼び出す必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

方程式のコード化

方程式をコード化する前に、それが pdepe ソルバーで想定される形式であることを確認する必要があります。

$c (x, t, u, \frac{\partial u}{\partial x}) \frac{\partial u}{\partial t} = x^{- m} \frac{\partial}{\partial x} (x^{m} f (x, t, u, \frac{\partial u}{\partial x})) + s (x, t, u, \frac{\partial u}{\partial x}) .$

この形式では、PDE の係数は行列値であり、方程式は次のようになります。

$[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}] \frac{\partial}{\partial t} [\begin{array}{c} u_{1} \\ u_{2} \end{array}] = \frac{\partial}{\partial x} [\begin{array}{c} 0.024 \frac{\partial u_{1}}{\partial x} \\ 0.170 \frac{\partial u_{2}}{\partial x} \end{array}] + [\begin{array}{c} - F (u_{1} - u_{2}) \\ F (u_{1} - u_{2}) \end{array}] .$

したがって、方程式の係数の値は次のようになります。

$m = 0$

$c (x, t, u, \frac{\partial u}{\partial x}) = [\begin{array}{c} 1 \\ 1 \end{array}]$ (対角値のみ)

$f (x, t, u, \frac{\partial u}{\partial x}) = [\begin{array}{c} 0.024 \frac{\partial u_{1}}{\partial x} \\ 0.170 \frac{\partial u_{2}}{\partial x} \end{array}]$

$s (x, t, u, \frac{\partial u}{\partial x}) = [\begin{array}{c} - F (u_{1} - u_{2}) \\ F (u_{1} - u_{2}) \end{array}]$

これで、方程式をコード化する関数を作成できるようになりました。この関数にはシグネチャ [c,f,s] = pdefun(x,t,u,dudx) がなければなりません。

x は独立空間変数。
t は独立時間変数。
u は、x および t について微分される従属変数。これは 2 要素ベクトルで、u(1) は $u_{1} (x, t)$ 、u(2) は $u_{2} (x, t)$ です。
dudx は空間偏導関数 $\partial u / \partial x$ 。これは 2 要素ベクトルで、dudx(1) は $\partial u_{1} / \partial x$ 、dudx(2) は $\partial u_{2} / \partial x$ です。
出力 c、f、および s は、pdepe で想定される標準 PDE 方程式形式の係数に対応。

結果として、この例の方程式は次の関数で表すことができます。

function [c,f,s] = pdefun(x,t,u,dudx)
c = [1; 1];
f = [0.024; 0.17] .* dudx;
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F];
end

(メモ: 関数はすべて例の最後にローカル関数として含まれます。)

初期条件のコード化

次に、初期条件を返す関数を記述します。初期条件は最初の時間値において適用され、 $u (x, t_{0})$ の値を任意の "x" の値に対して提供します。初期条件の数は方程式の数と等しくなければならないため、この問題では初期条件が 2 つあります。関数シグネチャ u0 = pdeic(x) を使用して関数を記述します。

初期条件は次のとおりです。

$u_{1} (x, 0) = 1,$

$u_{2} (x, 0) = 0 .$

対応する関数は次のようになります。

function u0 = pdeic(x)
u0 = [1; 0];
end

境界条件のコード化

次に、境界条件を評価する関数を記述します。

$\begin{array}{l} \frac{\partial}{\partial x} u_{1} (0, t) = 0, \\ u_{2} (0, t) = 0, \\ \frac{\partial}{\partial x} u_{2} (1, t) = 0, \\ u_{1} (1, t) = 1 . \end{array}$

区間 $a \leq x \leq b$ で提示される問題について、境界条件はすべての $t$ 、および $x = a$ または $x = b$ のいずれかに適用されます。ソルバーで想定される境界条件の標準形式は次のとおりです。

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

この形式で記述する場合、 $u$ の偏導関数の境界条件は流束 $f (x, t, u, \frac{\partial u}{\partial x})$ によって表す必要があります。したがって、この問題の境界条件は以下のとおりです。

$x = 0$ の場合、方程式は次のようになります。

$[\begin{array}{c} 0 \\ u_{2} \end{array}] + [\begin{array}{c} 1 \\ 0 \end{array}] \cdot [\begin{array}{c} 0.024 \frac{\partial u_{1}}{\partial x} \\ 0.170 \frac{\partial u_{2}}{\partial x} \end{array}] = 0 .$

係数は次のようになります。

$p_{L} (x, t, u) = [\begin{array}{c} 0 \\ u_{2} \end{array}],$

$q_{L} (x, t) = [\begin{array}{c} 1 \\ 0 \end{array}] .$

同様に、 $x = 1$ の場合、方程式は次のようになります。

$[\begin{array}{c} u_{1} - 1 \\ 0 \end{array}] + [\begin{array}{c} 0 \\ 1 \end{array}] \cdot [\begin{array}{c} 0.024 \frac{\partial u_{1}}{\partial x} \\ 0.170 \frac{\partial u_{2}}{\partial x} \end{array}] = 0 .$

係数は次のようになります。

$p_{R} (x, t, u) = [\begin{array}{c} u_{1} - 1 \\ 0 \end{array}],$

$q_{R} (x, t) = [\begin{array}{c} 0 \\ 1 \end{array}] .$

境界関数は関数シグネチャ [pl,ql,pr,qr] = pdebc(xl,ul,xr,ur,t) を使用しなければなりません。

入力 xl および ul は左境界の $u$ および $x$ に対応。
入力 xr および ur は右境界の $u$ および $x$ に対応。
t は独立時間変数。
出力 pl および ql は左境界 (この問題では $x = 0$ ) の $p_{L} (x, t, u)$ および $q_{L} (x, t)$ に対応。
出力 pr および qr は右境界 (この問題では $x = 1$ ) の $p_{R} (x, t, u)$ および $q_{R} (x, t)$ に対応。

この例の境界条件は次の関数で表されます。

function [pl,ql,pr,qr] = pdebc(xl,ul,xr,ur,t)
pl = [0; ul(2)];
ql = [1; 0];
pr = [ur(1)-1; 0];
qr = [0; 1];
end

解のメッシュの選択

この問題の解は、 $t$ が小さいときに急速に変化します。pdepe では、急激な変化を解決するのに相応しいタイムステップが選択されますが、出力プロットでその動作を表示するには、適切な出力時間を選択する必要があります。空間メッシュでは $0 \leq x \leq 1$ の両端において解に境界層があるため、そこにメッシュ点を指定して急激な変化を解決する必要があります。

x = [0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t = [0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];

方程式の求解

最後に、対称性 $m$ 、PDE 方程式、初期条件、境界条件、および $x$ と $t$ のメッシュを使用して方程式を解きます。

m = 0;
sol = pdepe(m,@pdefun,@pdeic,@pdebc,x,t);

pdepe は 3 次元配列 sol に解を返します。ここで、sol(i,j,k) は t(i) と x(j) で評価した解の k 番目の要素 $u_{k}$ を近似します。それぞれの解要素を別々の変数に抽出します。

u1 = sol(:,:,1);
u2 = sol(:,:,2);

解のプロット

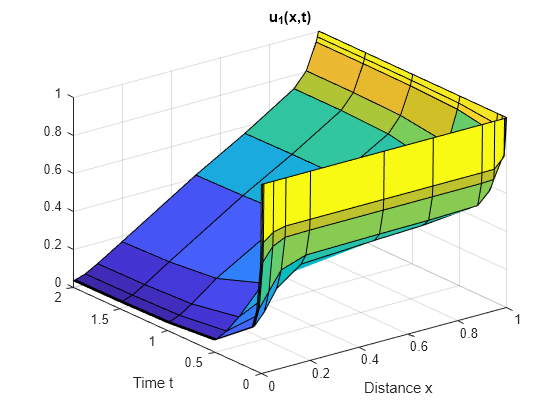
$x$ と $t$ の選択されたメッシュ点でプロットされた、 $u_{1}$ と $u_{2}$ の解の表面プロットを作成します。

surf(x,t,u1)
title('u_1(x,t)')
xlabel('Distance x')
ylabel('Time t')

Figure contains an axes object. The axes object with title u indexOf 1 baseline (x,t), xlabel Distance x, ylabel Time t contains an object of type surface.

surf(x,t,u2)
title('u_2(x,t)')
xlabel('Distance x')
ylabel('Time t')

Figure contains an axes object. The axes object with title u indexOf 2 baseline (x,t), xlabel Distance x, ylabel Time t contains an object of type surface.

ローカル関数

ここでは、PDE ソルバー pdepe が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function [c,f,s] = pdefun(x,t,u,dudx) % Equation to solve
c = [1; 1];
f = [0.024; 0.17] .* dudx;
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F];
end
% ---------------------------------------------
function u0 = pdeic(x) % Initial Conditions
u0 = [1; 0];
end
% ---------------------------------------------
function [pl,ql,pr,qr] = pdebc(xl,ul,xr,ur,t) % Boundary Conditions
pl = [0; ul(2)];
ql = [1; 0];
pr = [ur(1)-1; 0];
qr = [0; 1];
end
% ---------------------------------------------

参考

pdepe