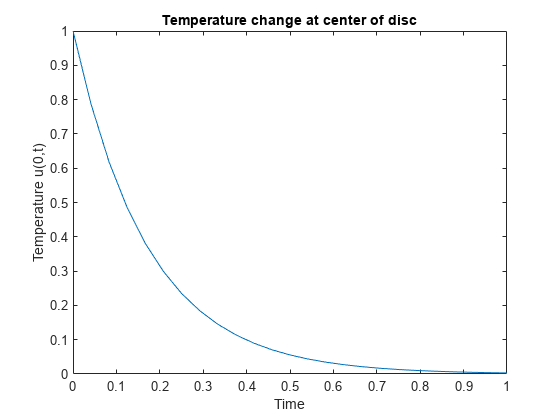
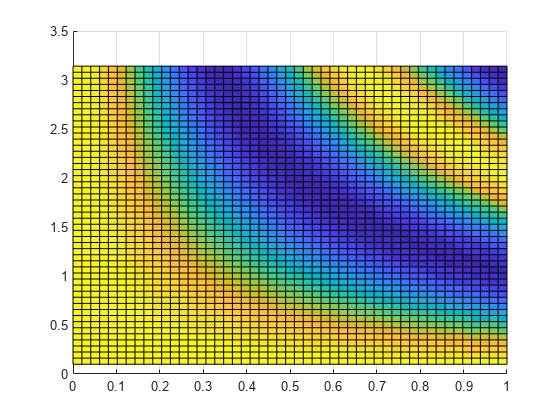
pdepe

1 次元の放物型および楕円型 PDE の求解

構文

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan)

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options)

[sol,tsol,sole,te,ie] = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options)

説明

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan) は、1 つの空間変数 x と時間 t をもつ放物型および楕円型 PDE 系を解きます。少なくとも 1 つの方程式は放物型でなければなりません。スカラー m は、問題の対称性 (スラブ、円柱または球面) を表します。求解する方程式は pdefun に、初期値は icfun に、境界条件は bcfun にそれぞれコード化されています。空間的に離散化して求める常微分方程式 (ODE) は、tspan に指定された各時点で、近似解を得るために積分されます。pdepe 関数は、xmesh で与えられるメッシュ上の解の値を返します。

例

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options) は options (関数 odeset を使用して作成) で定義された積分設定も使用します。たとえば、AbsTol オプションと RelTol オプションを使用して、絶対許容誤差と相対許容誤差を指定します。

例

[sol,tsol,sole,te,ie] = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options) は、(t,u(x,t)) の関数 (イベント関数) がゼロになる点も求めます。出力の te はイベント時点、sole はイベント時点における解、ie はトリガーされたイベントのインデックスです。tsol は、最初の終了イベントの前に tspan に指定された時間の列ベクトルです。

各イベント関数に対して、ゼロで積分を終了するかどうかと、ゼロクロッシングの方向を考慮するかどうかを指定します。これを行うには、@myEventFcn などの関数に odeset の Events オプションを設定し、対応する関数 [value,isterminal,direction] = myEventFcn(m,t,xmesh,umesh) を作成します。xmesh の入力は空間メッシュを含み、umesh はメッシュ点の解です。

例

すべて折りたたむ

円柱座標での熱方程式の求解

ライブスクリプトを開く

pdepe を使用して熱方程式を円柱座標で解き、解をプロットします。

角対称性をもつ円柱座標では、熱方程式は次のようになります。

$\frac{\partial u}{\partial t} = \frac{1}{x} \frac{\partial}{\partial x} (x \frac{\partial u}{\partial x}) .$

方程式は、時間 $t \geq 0$ における $0 \leq x \leq 1$ について定義されます。初期条件は、ベッセル関数 $J_{0} (x)$ とその最初のゼロ $n = 2.404825557695773$ によって次のように定義されます。

$u (x, 0) = J_{0} (nx) .$

この問題は円柱座標 (m = 1) にあるため、pdepe は $x = 0$ で対称条件を自動的に適用します。右境界条件は次のようになります。

$u (1, t) = J_{0} (n) e^{- n^{2} t} .$

初期条件と境界条件は、次の問題の解析解と整合するように選択されます。

$u (x, t) = J_{0} (nx) e^{- n^{2} t} .$

この方程式を MATLAB® で解くには、方程式、初期条件、境界条件をコード化し、適切な解のメッシュを選択してからソルバー pdepe を呼び出す必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

方程式のコード化

方程式は、コード化する前に pdepe ソルバーで想定される形式に書き換える必要があります。pdepe で想定される標準形式は次のとおりです。

$c (x, t, u, \frac{\partial u}{\partial x}) \frac{\partial u}{\partial t} = x^{- m} \frac{\partial}{\partial x} (x^{m} f (x, t, u, \frac{\partial u}{\partial x})) + s (x, t, u, \frac{\partial u}{\partial x}) .$

この形式で記述すると、PDE は次のようになります。

$\frac{\partial u}{\partial t} = x^{- 1} \frac{\partial}{\partial x} (x^{1} \frac{\partial u}{\partial x})$

適切な形式の方程式を使用すると、関連する項を読み取ることができます。

$m = 1$
$c (x, t, u, \frac{\partial u}{\partial x}) = 1$
$f (x, t, u, \frac{\partial u}{\partial x}) = \frac{\partial u}{\partial x}$
$s (x, t, u, \frac{\partial u}{\partial x}) = 0$

これで、方程式をコード化する関数を作成できるようになりました。この関数にはシグネチャ [c,f,s] = heatcyl(x,t,u,dudx) がなければなりません。

x は独立空間変数。
t は独立時間変数。
u は、x および t について微分される従属変数。
dudx は空間偏導関数 $\partial u / \partial x$ 。
出力 c、f、および s は、pdepe で想定される標準 PDE 方程式形式の係数に対応。これらの係数は、入力変数 x、t、u、および dudx によってコード化されます。

結果として、この例の方程式は次の関数で表すことができます。

function [c,f,s] = heatcyl(x,t,u,dudx)
c = 1;
f = dudx;
s = 0;
end

(メモ: 関数はすべて例の最後にローカル関数として含まれます。)

初期条件のコード化

次に、初期条件を返す関数を記述します。初期条件は、最初の時間値 tspan(1) で適用されます。この関数にはシグネチャ u0 = heatic(x) がなければなりません。

$u (x, 0) = J_{0} (nx)$ に対応する関数は次のようになります。

function u0 = heatic(x)
n = 2.404825557695773;
u0 = besselj(0,n*x);
end

境界条件のコード化

次に、境界条件を評価する関数を記述します。

$u (1, t) = J_{0} (n) e^{- n^{2} t} .$

この問題は円柱座標 (m = 1) にあるため、pdepe は $x = 0$ で対称条件を自動的に適用します。したがって、左境界条件を指定する必要はありません。

区間 $a \leq x \leq b$ で提示される問題について、境界条件はすべての $t$ 、および $x = a$ または $x = b$ のいずれかに適用されます。ソルバーで想定される境界条件の標準形式は次のとおりです。

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

この形式で記述する場合、 $u$ の偏導関数の境界条件は流束 $f (x, t, u, \frac{\partial u}{\partial x})$ によって表す必要があります。そのため、この問題の右境界条件は次のようになります。

$u (1, t) - J_{0} (n) e^{- n^{2} t} + 0 \cdot f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

境界関数には関数シグネチャ [pl,ql,pr,qr] = heatbc(xl,ul,xr,ur,t) がなければなりません。

入力 xl および ul は左境界の $u$ および $x$ に対応。
入力 xr および ur は右境界の $u$ および $x$ に対応。
t は独立時間変数。
出力 pl および ql は左境界 (この問題では $x = 0$ ) の $p_{L} (x, t, u)$ および $q_{L} (x, t)$ に対応。
出力 pr および qr は右境界 (この問題では $x = 1$ ) の $p_{R} (x, t, u)$ および $q_{R} (x, t)$ に対応。

この例の境界条件は次の関数で表されます。

function [pl,ql,pr,qr] = heatbc(xl,ul,xr,ur,t)
n = 2.404825557695773;
pl = 0; %ignored by solver since m=1
ql = 0; %ignored by solver since m=1
pr = ur-besselj(0,n)*exp(-n^2*t);
qr = 0; 
end

解のメッシュの選択

方程式を解く前に、メッシュ点 $(t, x)$ を、pdepe が解を評価する点として指定する必要があります。これらは、ベクトル t と x に設定します。ベクトル t と x は、ソルバーの中で異なる役割をもちます。特に求解のコストと精度は、ベクトル x の長さに強く依存します。しかし、ベクトル t の値にはあまり影響を受けません。

この問題では、x と t の両方の空間区間 [0,1] 内に等間隔に配置された 25 個の点をもつメッシュを使用します。

x = linspace(0,1,25);
t = linspace(0,1,25);

方程式の求解

最後に、対称性 m、PDE 方程式、初期条件、境界条件、および x と t のメッシュを使用して方程式を解きます。

m = 1;
sol = pdepe(m,@heatcyl,@heatic,@heatbc,x,t);

pdepe は 3 次元配列 sol に解を返します。ここで、sol(i,j,k) は t(i) と x(j) で評価した解の k 番目の要素 $u_{k}$ を近似します。u0 が各解要素の初期条件を指定するため、sol のサイズは length(t) x length(x) x length(u0) となります。この問題では u の要素は 1 つのみであるため、sol は 25 行 25 列の行列になりますが、通常はコマンド u = sol(:,:,k) を使用して k 番目の解要素を抽出できます。

最初の解要素を sol から抽出します。

u = sol(:,:,1);

解のプロット

解の表面プロットを作成します。この問題はディスク上の円柱座標で提示されているため、x の値は中心からの距離に応じたディスク上の温度を示し、t の値は特定の位置における温度の経時変化を示します。

surf(x,t,u)
xlabel("x")
ylabel("t")
zlabel("u(x,t)")
view([150 25])

Figure contains an axes object. The axes object with xlabel x, ylabel t contains an object of type surface.

ディスクの中心 ( $x = 0$ ) の温度変化をプロットします。

plot(t,sol(:,1))
xlabel("Time")
ylabel("Temperature u(0,t)")
title("Temperature change at center of disc")

Figure contains an axes object. The axes object with title Temperature change at center of disc, xlabel Time, ylabel Temperature u(0,t) contains an object of type line.

ローカル関数

ここでは、PDE ソルバー pdepe が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function [c,f,s] = heatcyl(x,t,u,dudx)
c = 1;
f = dudx;
s = 0;
end
%----------------------------------------------
function u0 = heatic(x)
n = 2.404825557695773;
u0 = besselj(0,n*x);
end
%----------------------------------------------
function [pl,ql,pr,qr] = heatbc(xl,ul,xr,ur,t)
n = 2.404825557695773;
pl = 0; %ignored by solver since m=1
ql = 0; %ignored by solver since m=1
pr = ur-besselj(0,n)*exp(-n^2*t);
qr = 0; 
end
%----------------------------------------------

イベントログを使用した振動 PDE の求解

ライブスクリプトを開く

偏微分方程式を解き、イベント関数を使用して振動解のゼロクロッシングをログに記録します。

次の方程式を考えます。

$\frac{1}{x} \frac{\partial u}{\partial t} = \frac{\partial}{\partial x} (\frac{1}{t} u) .$

方程式は $0 \leq x \leq 1$ および $t \geq 0.1$ に対して定義されます。初期条件は次のとおりです。

$u (x, 0.1) = 1 .$

境界条件は次のとおりです。

$u (0, t) = 1,$

$u (1, t) = \cos (π t) .$

さらに、解のゼロクロッシングにも注目します。

この問題を MATLAB で解くには、方程式、初期条件、境界条件、イベント関数をコード化し、ソルバー pdepe を呼び出す前に適切な解のメッシュを選択する必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

方程式のコード化

方程式は、コード化する前に pdepe ソルバーで想定される形式に書き換える必要があります。pdepe で想定される標準形式は次のとおりです。

PDE 方程式は既に次の形式になっています。

$\frac{1}{x} \frac{\partial u}{\partial t} = \frac{\partial}{\partial x} (\frac{1}{t} u) .$

そのため、関連する次の項を読み取ることができます。

$m = 0$
$c (x, t, u, \frac{\partial u}{\partial x}) = \frac{1}{x}$
$f (x, t, u, \frac{\partial u}{\partial x}) = \frac{1}{t} u$
$s (x, t, u, \frac{\partial u}{\partial x}) = 0$

これで、方程式をコード化する関数を作成できるようになりました。この関数にはシグネチャ [c,f,s] = oscpde(x,t,u,dudx) がなければなりません。

x は独立空間変数。
t は独立時間変数。
u は、x および t について微分される従属変数。
dudx は空間偏導関数 $\partial u / \partial x$ 。
出力 c、f、および s は、pdepe で想定される標準 PDE 方程式形式の係数に対応。これらの係数は、入力変数 x、t、u、および dudx によってコード化されます。

結果として、この例の方程式は次の関数で表すことができます。

function [c,f,s] = oscpde(x,t,u,dudx)
c = 1/x;
f = u/t;
s = 0;
end

(メモ: 関数はすべて例の最後にローカル関数として含まれます。)

初期条件のコード化

次に、初期条件を返す関数を記述します。初期条件は、最初の時間値 tspan(1) で適用されます。この関数にはシグネチャ u0 = oscic(x) がなければなりません。

$u (x, 0.1) = 1$ に対応する関数は次のようになります。

function u0 = oscic(x)
u0 = 1;
end

境界条件のコード化

次に、境界条件を評価する関数を記述します。

$u (0, t) = 1,$

$u (1, t) = \cos (π t) .$

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

この形式で記述すると、この問題の境界条件は次のようになります。

$u (0, t) - 1 + 0 \cdot f (x, t, u, \frac{\partial u}{\partial x}) = 0,$

$u (1, t) - \cos (π t) + 0 \cdot f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

境界関数には関数シグネチャ [pl,ql,pr,qr] = oscbc(xl,ul,xr,ur,t) がなければなりません。

入力 xl および ul は左境界の $x$ および $u$ に対応。
入力 xr および ur は右境界の $x$ および $u$ に対応。
t は独立時間変数。
出力 pl および ql は左境界 (この問題では $x = 0$ ) の $p_{L} (x, t, u)$ および $q_{L} (x, t)$ に対応。
出力 pr および qr は右境界 (この問題では $x = 1$ ) の $p_{R} (x, t, u)$ および $q_{R} (x, t)$ に対応。

この例の境界条件は次の関数で表されます。

function [pl,ql,pr,qr] = oscbc(xl,ul,xr,ur,t)
pl = ul - 1;
ql = 0;
pr = ur - cos(pi*t);
qr = 0;
end

イベント関数のコード化

イベント関数を使用して、積分の解のゼロクロッシングをログに記録します。イベント関数には [value,isterminal,direction] = pdevents(m,t,xmesh,umesh) の関数シグネチャがあります。

m は pdepe の最初の入力として指定された座標の対称性。
t は現在の時間 (スカラー)。
xmesh は空間メッシュ。
umesh にはメッシュ点での解が含まれる。
value は対象の方程式であり、通常は解 umesh で表される。value が 0 のときにイベントが発生します。
isterminal は、イベントが積分を停止するかどうかを指定。isterminal が 0 の場合、イベントはログに記録されますが、積分は停止しません。isterminal が 1 の場合、積分はイベント発生時に停止します。
direction はゼロクロッシングの方向を指定。1 の場合、正の傾きをもつゼロクロッシングのみがイベントをトリガーします。-1 の場合、ゼロクロッシングは負の傾きをもたなければなりません。0 の場合、すべてのゼロクロッシングがイベントをトリガーします。

積分の各時点で、ソルバーがイベント関数を呼び出してゼロクロッシングをチェックします。すべてのゼロクロッシングをログに記録するには、value が解ベクトル umesh の符号の変化を検出する必要があります。この例のイベントは終了イベントでなく、ゼロクロッシングはすべての傾きで発生する可能性があるため、isterminal と direction を同じサイズのゼロのベクトルとして指定します。

この問題のイベント関数は次のようになります。

function [value,isterminal,direction] = pdevents(m,t,xmesh,umesh)
value = umesh;
isterminal = zeros(size(umesh));
direction = zeros(size(umesh));
end

解のメッシュの選択

方程式を解く前に、メッシュ点 $(t, x)$ を、pdepe が解を評価する点として指定する必要があります。この問題では、 $0 \leq x \leq 1$ および $0.1 \leq t \leq 1$ の区間内で 50 点の細かいメッシュを使用します。細かいメッシュを使用することで、振動解の分解能が向上します。

x = linspace(0,1,50);
t = linspace(0.1,pi,50);

方程式の求解

最後に、対称性 m、PDE 方程式、初期条件、境界条件、イベント関数、および x と t のメッシュを使用して方程式を解きます。odeset を使用してイベント関数を参照するオプション構造体を作成し、pdepe への最後の入力引数として構造体を渡します。イベント関数とソルバーの両方から情報を返す次の 5 つの出力引数を指定します。

sol は pdepe によって計算された解です。
tsol は終了イベント前の時間のベクトルです。終了イベントがない場合、tsol は t と等しくなります。
sole は各イベントの時点での解です。
te は各イベントの時間です。
ie は各イベントのインデックスです。イベント関数では values = umesh であるため、ie は、各タイムステップでイベントをトリガーした umesh のインデックスを返します。

m = 0;
options = odeset(Events=@pdevents);
[sol,tsol,sole,te,ie] = pdepe(m,@oscpde,@oscic,@oscbc,x,t,options);

解を行列 u として抽出します。

u = sol(:,:,1);

解のプロット

解の表面プロットを作成し、プロットを上方から表示します。

surf(x,t,u)
view(2)

Figure contains an axes object. The axes object contains an object of type surface.

参照用に表面 $f (x, t) = 0$ を使用して、イベントが発生した点をプロットします。出力されたインデックスベクトル ie は、イベントの位置を選択する際に役立ちます。式 x(ie)' によりイベントが発生した位置の x 値が得られ、式 sole(x==x(ie)') により対応する解の値が得られます。

view([39 30])
xlabel("x")
ylabel("t")
zlabel("u(x,t)")
hold on
plot3(x(ie)',te,sole(x==x(ie)'),'r*')
surf(x,t,zeros(size(u)),EdgeColor="flat")
hold off

Figure contains an axes object. The axes object with xlabel x, ylabel t contains 3 objects of type surface, line. One or more of the lines displays its values using only markers

ローカル関数

ここでは、PDE ソルバー pdepe が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function [c,f,s] = oscpde(x,t,u,dudx)
c = 1/x;
f = u/t;
s = 0;
end
%----------------------------------------------
function u0 = oscic(x)
u0 = 1;
end
%----------------------------------------------
function [pl,ql,pr,qr] = oscbc(xl,ul,xr,ur,t)
pl = ul - 1;
ql = 0;
pr = ur - cos(pi*t);
qr = 0;
end
%----------------------------------------------
function [value, isterminal, direction] = pdevents(m,t,xmesh,umesh)
value = umesh;
isterminal = zeros(size(umesh));
direction = zeros(size(umesh));
end
%----------------------------------------------

入力引数

すべて折りたたむ

`m` — 対称性の定数
`0` | `1` | `2`

対称性の定数。次の表のいずれかの値として指定します。m は、pdefun で指定される方程式の問題のタイプを指定します。方程式を pdepe が想定する形式に書き換えた後に、m の値を方程式から読み取ります。

値説明流束のラプラシアン

値	説明	流束のラプラシアン
`0`	対称性のない 1 次元直交座標	$Δ f = \frac{\partial^{2} f}{\partial x^{2}}$
`1`	方位角対称性をもつ 2 次元円柱座標	$Δ f = \frac{1}{ρ} \frac{\partial}{\partial ρ} (ρ \frac{\partial f}{\partial ρ}) + \frac{1}{ρ^{2}} \frac{\partial^{2} f}{\partial φ^{2}}$ , $\frac{\partial f}{\partial φ} = 0$ (方位角対称性)。
`2`	方位角および天頂角対称性をもつ 3 次元球面座標	$Δ f = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial f}{\partial r}) + \frac{1}{r^{2} \sin θ} \frac{\partial}{\partial θ} (\sin θ \frac{\partial f}{\partial θ}) + \frac{1}{r^{2} \sin^{2} θ} \frac{\partial^{2} f}{\partial φ^{2}}$ , $\frac{\partial f}{\partial θ} = \frac{\partial f}{\partial φ} = 0$ (方位角および天頂角対称性)。

0

対称性のない 1 次元直交座標

Δ f = \frac{\partial^{2} f}{\partial x^{2}}

1

方位角対称性をもつ 2 次元円柱座標

$Δ f = \frac{1}{ρ} \frac{\partial}{\partial ρ} (ρ \frac{\partial f}{\partial ρ}) + \frac{1}{ρ^{2}} \frac{\partial^{2} f}{\partial φ^{2}}$ ,

$\frac{\partial f}{\partial φ} = 0$ (方位角対称性)。

2

方位角および天頂角対称性をもつ 3 次元球面座標

$Δ f = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial f}{\partial r}) + \frac{1}{r^{2} \sin θ} \frac{\partial}{\partial θ} (\sin θ \frac{\partial f}{\partial θ}) + \frac{1}{r^{2} \sin^{2} θ} \frac{\partial^{2} f}{\partial φ^{2}}$ ,

$\frac{\partial f}{\partial θ} = \frac{\partial f}{\partial φ} = 0$ (方位角および天頂角対称性)。

m > 0 の場合、pdepe では、左空間境界 a が ≥ 0 である必要があり、原点での座標の不連続性を考慮して自動的に左境界条件を適用します。その場合、pdepe は、bcfun で指定されたすべての左境界条件を無視します。

`pdefun` — 方程式用の PDE 関数
関数ハンドル

方程式用の PDE 関数。PDE の係数を定義する関数ハンドルとして指定します。

pdefun は、次の形式の PDE の係数をエンコードします。

方程式の項は次のとおりです。

$f (x, t, u, \frac{\partial u}{\partial x})$ は流束項。
$s (x, t, u, \frac{\partial u}{\partial x})$ はソース項。
時間に関連する偏導関数の結合は、対角行列 $c (x, t, u, \frac{\partial u}{\partial x})$ による乗算に限定されます。この行列の対角要素は、ゼロまたは正になります。ゼロの要素は楕円方程式に対応し、その他すべての要素は放物線方程式に対応します。少なくとも 1 つの放物型方程式は存在しなければなりません。放物型方程式に対応する c の要素は、x のそれらの値がメッシュ点に存在すれば、x の孤立点をなくせます。
物質の境界による c や s の不連続は、メッシュ点が各境界に置かれている場合に使われます。

これらの PDE は t₀ ≤ t ≤ t_f かつ a ≤ x ≤ b です。値 tspan(1) および tspan(end) は t₀ および t_f に対応し、xmesh(1) および xmesh(end) は a および b に対応します。区間 [a,b] は有限でなければなりません。m は 0、1、2 のいずれかで、それぞれスラブ、円柱、球面対称性に対応します。m > 0 の場合、a ≥ 0 でなければなりません。

方程式のコード化

係数 c、f、および s の値を計算する関数 pdefun を記述します。次の関数シグネチャを使用します。

[c,f,s] = pdefun(x,t,u,dudx)

pdefun への入力引数は、スカラー x および t とベクトル u および dudx です。ベクトル u は解 u を近似し、dudx は x に関するその偏微分を近似します。出力引数 c、f、および s は、方程式の数と同じ数の要素をもつ列ベクトルです。c は、行列 c の対角要素を格納します。

例

熱方程式 $\frac{\partial u}{\partial t} = \frac{\partial^{2} u}{\partial x^{2}}$ は、ソルバーが想定する次のような形式に書き換えることができます。

$1 \cdot \frac{\partial u}{\partial t} = x^{0} \frac{\partial}{\partial x} (x^{0} \frac{\partial u}{\partial x}) .$

この形式では、係数の値を m = 0、c = 1、f = ∂u/∂x、および s = 0 として読み取ることができます。この方程式の関数は次のようになります。

function [c,f,s] = heatpde(x,t,u,dudx)  
  c = 1;
  f = dudx;
  s = 0;
end

データ型: function_handle

`icfun` — 初期条件関数
関数ハンドル

初期条件関数。初期条件を定義する関数ハンドルとして指定します。

t = t₀ およびすべての x に対して、解の要素は次の型の初期条件を満たします。

$u (x, t_{0}) = u_{0} (x) .$

初期条件のコード化

初期条件を定義する関数 icfun を記述します。次の関数シグネチャを使用します。

function u0 = icfun(x)

引数 x と共に呼び出すと、関数 icfun は列ベクトル u0 の x における解要素の初期値を計算し、返します。u0 の要素数は方程式の数と同じです。

例

定数の初期条件 $u (x, 0) = 1 / 2$ は、次の関数に対応します。

function u0 = heatic(x)
  u0 = 0.5;
end

データ型: function_handle

`bcfun` — 境界条件関数
関数ハンドル

境界条件関数。境界条件を定義する関数ハンドルとして指定します。

すべての t および x = a または x = b に対して、解の要素は次の型の境界条件を満たします。

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0.$

q の要素は、ゼロまたは非ゼロのいずれかです。境界条件が ∂u/∂x ではなく、流束の項 f で表されることに注意してください。また、2 つの係数のうち p のみが u に依存します。

境界条件のコード化

境界条件の項 p および q を定義する関数 bcfun を記述します。次の関数シグネチャを使用します。

function [pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)

ul は左境界 xl = a の近似解であり、ur は右境界 xr = b の近似解です。
pl と ql は xl で計算した p と q に対応する列ベクトルです。同様に、pr と qr は xr に対応します。
出力 pl、ql、pr、および qr の要素数は方程式の数と同じです。

m > 0 かつ a = 0 のとき、x = 0 の近傍での解の制約条件は、流束 f が a = 0 でゼロになる必要があります。pdepe は、この境界条件を自動的に適用し、pl と ql に返される値を無視します。

例

区間 $0 \leq x \leq 1$ での境界条件 $u (0, t) = 0, u (1, t) = 1$ について考えます。ソルバーが想定する形式では、境界条件は次のようになります。

$\begin{array}{l} u (0, t) + 0 \cdot f (0, t, u, \frac{\partial u}{\partial x}) = 0, \\ u (1, t) - 1 + 0 \cdot f (0, t, u, \frac{\partial u}{\partial x}) = 0. \end{array}$

この形式では、どちらの q 項もゼロであることは明らかです。p 項は、u の値を反映するために非ゼロです。対応する関数は次のようになります。

function [pl,ql,pr,qr] = heatbc(xl,ul,xr,ur,t)
  pl = ul;
  ql = 0;
  pr = ur - 1;
  qr = 0;
end

データ型: function_handle

`xmesh` — 空間メッシュ
ベクトル

空間メッシュ。tspan のすべての値に対して、数値解が必要な点を指定するベクトル [x0 x1 ... xn] として指定します。解の 2 次近似は、xmesh に指定されたメッシュ上で行います。pdepe は、x でメッシュの選択を自動的には "行いません"。ユーザーは、固定された適切なメッシュを xmesh に与える必要があります。

xmesh の要素は、x0 < x1 < ... < xn を満たさなければなりません。一般に、解の変化が激しい部分では、密なメッシュ点を使うことを推奨します。xmesh の長さは >=3 でなければならず、解の計算コストは xmesh の長さに強く依存します。

不連続性を伴う問題では、各部分区間内で問題が滑らかになるように、不連続点にメッシュ点を配置する必要があります。ただし、m > 0 の場合、座標特異点のために、x = 0 の近くで細かいメッシュを使う必要はありません。

例: xmesh = linspace(0,5,25) は 0 と 5 の間の 25 点の空間メッシュを使用します。

データ型: single | double

`tspan` — 積分の時間範囲
ベクトル

積分の時間範囲。xmesh のすべての値に対して、解が必要な点を指定するベクトル [t0 t1 ... tf] として指定します。関数 pdepe は ODE ソルバーを使って、時間積分を行うときに、動的にタイムステップと式を選択します。tspan の要素は、ユーザーが参照する位置を指定するのみのものなので、tspan の長さによっては解の計算コストに若干の差が出ます。

tspan の要素は、t0 < t1 < ... < tf を満たさなければなりません。tspan の長さは >=3 でなければなりません。

例: tspan = linspace(0,5,5) は 0 と 5 の間の 5 つの時間点を使用します。

データ型: single | double

`options` — オプション構造体
構造体配列

オプション構造体。構造体配列として指定します。オプション構造体の作成または変更を行うには、関数 odeset を使用します。odeset のいずれのオプションも設定できますが、次のオプションは PDE を解くときに pdepe でオーバーライドされます。

Mass
MStateDependence
MvPattern
MassSingular
Jacobian
JPattern
Vectorized

例: options = odeset(RelTol=1e-5) は 1e-5 の相対許容誤差を指定します。

データ型: struct

出力引数

すべて折りたたむ

`sol` — 解の配列
3 次元配列

解の配列。3 次元配列として返されます。

関数 pdepe は、解を多次元配列として返します。u_i = ui = sol(:,:,i) は、解ベクトル u の i 番目の要素への近似になります。要素 ui(j,k) = sol(j,k,i) は、(t,x) = (tspan(j),xmesh(k)) で u_i を近似します。

ui = sol(j,:,i) は、時点 tspan(j) とメッシュ点 xmesh(:) で、解の要素 i を近似します。関数 pdeval を使用して、xmesh に含まれない点で、近似とその偏導関数 ∂u_i/∂x を計算します。詳細については、pdeval を参照してください。

`tsol` — 解の時点
列ベクトル

解の時点。最初の終了イベントの前に tspan に指定された時間の列ベクトルとして返されます。

`sole` — イベント時点での解
配列

イベント時点での解。配列として返されます。te のイベント時点は sole に返された解に対応し、ie は発生したイベントを指定します。

`te` — イベント時点
列ベクトル

イベント時点。列ベクトルとして返されます。te のイベント時点は sole に返された解に対応し、ie は発生したイベントを指定します。

`ie` — トリガーされるイベント関数のインデックス
列ベクトル

トリガーされるイベント関数のインデックス。列ベクトルとして返されます。te のイベント時点は sole に返された解に対応し、ie は発生したイベントを指定します。

ヒント

uji = sol(j,:,i) が時間 tspan(j) とメッシュ点 xmesh で解の要素 i を近似する場合、pdeval は、点 xout の配列において近似値とその偏導関数 ∂u_i/∂x を評価して、それらを uout および duoutdx に返します ([uout,duoutdx] = pdeval(m,xmesh,uji,xout))。関数 pdeval は、流束ではなく偏導関数 ∂u_i/∂x を評価します。流束は連続ですが、構成物の接続点では偏導関数は不連続になる場合があるからです。

アルゴリズム

時間積分は、ode15s ソルバーを使用して行います。pdepe は、PDE が楕円方程式を含んでいる場合に生じる微分代数方程式を解くため、また指定したスパースパターンをもつヤコビアンを取り扱うために、ode15s の機能を使用します。

離散化の後、楕円方程式から代数方程式が生成されます。楕円方程式に対応した初期条件の要素が、離散化と矛盾している場合、関数 pdepe は、時間積分を始める前にそれらの調整を試みます。このため、最初の時点に対して返される解は、他の時点のものと同程度の離散化誤差をもっています。メッシュが十分細かい場合、関数 pdepe は与えられた初期条件に近い整合性のある初期条件を検出することができます。関数 pdepe が、整合性のある初期条件を見つけることが困難であるというメッセージを表示する場合は、メッシュをより細かく分割してください。放物線方程式に対応する初期条件ベクトルの要素の調整は必要ありません。

参照

[1] Skeel, R. D. and M. Berzins, "A Method for the Spatial Discretization of Parabolic Equations in One Space Variable," SIAM Journal on Scientific and Statistical Computing, Vol. 11, 1990, pp.1–32.

拡張機能

すべて展開する

スレッドベースの環境
MATLAB® の `backgroundPool` を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の `ThreadPool` を使用してコードを高速化します。

バージョン履歴

R2006a より前に導入

すべて展開する

R2025a: 出力関数およびその他の `odeset` のオプションを指定

pdepe 関数を使用するときに、出力関数を含むすべての odeset のオプションを指定できるようになりました。ただし、一部のオプションは、解を求める PDE を定義するときに pdepe でオーバーライドされます。詳細については、options を参照してください。

以前は、RelTol、AbsTol、NormControl、InitialStep、MaxStep、および Events のオプションのみが pdepe でサポートされていました。

参考

pdeval | ode15s | odeset | odeget

pdepe

構文

説明

例

円柱座標での熱方程式の求解

イベント ログを使用した振動 PDE の求解

入力引数

m — 対称性の定数 0 | 1 | 2

pdefun — 方程式用の PDE 関数 関数ハンドル

方程式のコード化

例

icfun — 初期条件関数 関数ハンドル

初期条件のコード化

例

bcfun — 境界条件関数 関数ハンドル

境界条件のコード化

例

xmesh — 空間メッシュ ベクトル

tspan — 積分の時間範囲 ベクトル

options — オプション構造体 構造体配列

出力引数

sol — 解の配列 3 次元配列

tsol — 解の時点 列ベクトル

sole — イベント時点での解 配列

te — イベント時点 列ベクトル

ie — トリガーされるイベント関数のインデックス 列ベクトル

ヒント

アルゴリズム

参照

拡張機能

スレッドベースの環境 MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

バージョン履歴

R2025a: 出力関数およびその他の odeset のオプションを指定

参考

トピック

イベントログを使用した振動 PDE の求解

`m` — 対称性の定数
`0` | `1` | `2`

`pdefun` — 方程式用の PDE 関数
関数ハンドル

`icfun` — 初期条件関数
関数ハンドル

`bcfun` — 境界条件関数
関数ハンドル

`xmesh` — 空間メッシュ
ベクトル

`tspan` — 積分の時間範囲
ベクトル

`options` — オプション構造体
構造体配列

`sol` — 解の配列
3 次元配列

`tsol` — 解の時点
列ベクトル

`sole` — イベント時点での解
配列

`te` — イベント時点
列ベクトル

`ie` — トリガーされるイベント関数のインデックス
列ベクトル

スレッドベースの環境
MATLAB® の `backgroundPool` を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の `ThreadPool` を使用してコードを高速化します。

R2025a: 出力関数およびその他の `odeset` のオプションを指定