単一の PDE の求解

ライブスクリプトを開く

この例では、単一の PDE の定式化、計算、および解のプロット方法を説明します。

次の偏微分方程式を考えます。

$π^{2} \frac{\partial u}{\partial t} = \frac{\partial^{2} u}{\partial x^{2}} .$

この方程式は、時間 $t \geq 0$ について区間 $0 \leq x \leq 1$ で定義されます。 $t = 0$ で、解は次の初期条件を満たします。

$u (x, 0) = \sin (π x) .$

また、 $x = 0$ および $x = 1$ で、解は以下の境界条件を満たします。

$u (0, t) = 0,$

$π e^{- t} + \frac{\partial u}{\partial x} (1, t) = 0 .$

この方程式を MATLAB® で解くには、方程式、初期条件、および境界条件をコード化し、適切な解のメッシュを選択してから、ソルバー pdepe を呼び出す必要があります。(ここで行ったように) 必要な関数をファイルの最後にローカル関数として含めることも、あるいは個別の名前付きファイルとして MATLAB パスのディレクトリに保存することもできます。

方程式のコード化

方程式は、コード化する前に pdepe ソルバーで想定される形式に書き換える必要があります。pdepe で想定される標準形式は次のとおりです。

$c (x, t, u, \frac{\partial u}{\partial x}) \frac{\partial u}{\partial t} = x^{- m} \frac{\partial}{\partial x} (x^{m} f (x, t, u, \frac{\partial u}{\partial x})) + s (x, t, u, \frac{\partial u}{\partial x})$ .

この形式で記述すると、PDE は次のようになります。

$π^{2} \frac{\partial u}{\partial t} = x^{0} \frac{\partial}{\partial x} (x^{0} \frac{\partial u}{\partial x}) + 0$ .

適切な形式の方程式を使用すると、関連する項を読み取ることができます。

$m = 0$

$c (x, t, u, \frac{\partial u}{\partial x}) = π^{2}$

$f (x, t, u, \frac{\partial u}{\partial x}) = \frac{\partial u}{\partial x}$

$s (x, t, u, \frac{\partial u}{\partial x}) = 0$

これで、方程式をコード化する関数を作成できるようになりました。この関数にはシグネチャ [c,f,s] = pdex1pde(x,t,u,dudx) がなければなりません。

x は独立空間変数。
t は独立時間変数。
u は、x および t について微分される従属変数。
dudx は空間偏導関数 $\partial u / \partial x$ 。
出力 c、f、および s は、pdepe で想定される標準 PDE 方程式形式の係数に対応。これらの係数は、入力変数 x、t、u、および dudx によってコード化されます。

結果として、この例の方程式は次の関数で表すことができます。

function [c,f,s] = pdex1pde(x,t,u,dudx)
c = pi^2;
f = dudx;
s = 0;
end

(メモ: 関数はすべて例の最後にローカル関数として含まれます。)

初期条件のコード化

次に、初期条件を返す関数を記述します。初期条件は、最初の時間値 tspan(1) で適用されます。この関数にはシグネチャ u0 = pdex1ic(x) がなければなりません。

対応する関数は次のようになります。

function u0 = pdex1ic(x)
u0 = sin(pi*x);
end

境界条件のコード化

次に、境界条件を評価する関数を記述します。区間 $a \leq x \leq b$ で提示される問題について、境界条件はすべての $t$ 、および $x = a$ または $x = b$ のいずれかに適用されます。ソルバーで想定される境界条件の標準形式は次のとおりです。

$p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0 .$

この標準形式で境界条件を書き直し、係数値を読み取ります。

$x = 0$ の場合、方程式は次のようになります。

$u (0, t) = 0 \to u + 0 \cdot \frac{\partial u}{\partial x} = 0 .$

係数は次のようになります。

$p (0, t, u) = u$
$q (0, t) = 0$

$x = 1$ の場合、方程式は次のようになります。

$π e^{- t} + \frac{\partial u}{\partial x} (1, t) = 0 \to π e^{- t} + 1 \cdot \frac{\partial u}{\partial x} (1, t) = 0 .$

係数は次のようになります。

$p (1, t, u) = π e^{- t}$
$q (1, t) = 1$

境界条件関数は $f (x, t, u, \frac{\partial u}{\partial x})$ によって表現され、この項は既にメインの PDE 関数で定義されているため、方程式のこの部分を境界条件関数内で指定する必要はありません。 $p (x, t, u)$ および $q (x, t)$ の値のみを各境界で指定する必要があります。

境界関数は関数シグネチャ [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t) を使用しなければなりません。

入力 xl および ul は左境界の $u$ および $x$ に対応。
入力 xr および ur は右境界の $u$ および $x$ に対応。
t は独立時間変数。
出力 pl および ql は左境界 (この問題では $x = 0$ ) の $p (x, t, u)$ および $q (x, t)$ に対応。
出力 pr および qr は右境界 (この問題では $x = 1$ ) の $p (x, t, u)$ および $q (x, t)$ に対応。

この例の境界条件は次の関数で表されます。

function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
pl = ul;
ql = 0;
pr = pi * exp(-t);
qr = 1;
end

解のメッシュの選択

方程式を解く前に、メッシュ点 $(t, x)$ を、pdepe が解を評価する点として指定する必要があります。これらは、ベクトル t と x に設定します。ベクトル t と x は、ソルバーの中で異なる役割をもちます。特に求解のコストと精度は、ベクトル x の長さに強く依存します。しかし、ベクトル t の値にはあまり影響を受けません。

この問題では、空間区間 [0,1] 内で等間隔に配置された 20 個の点をもつメッシュと、時間区間 [0,2] からの t の 5 つの値を使用します。

x = linspace(0,1,20);
t = linspace(0,2,5);

方程式の求解

最後に、対称性 m、PDE 方程式、初期条件、境界条件、および x と t のメッシュを使用して方程式を解きます。

m = 0;
sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);

pdepe は 3 次元配列 sol に解を返します。ここで、sol(i,j,k) は t(i) と x(j) で評価した解の k 番目の要素 $u_{k}$ を近似します。u0 が各解要素の初期条件を指定するため、sol のサイズは length(t) x length(x) x length(u0) となります。この問題では、u の要素は 1 つのみであるため、sol は 5 行 20 列の行列になりますが、通常はコマンド u = sol(:,:,k) を使用して k 番目の解要素を抽出できます。

最初の解要素を sol から抽出します。

u = sol(:,:,1);

解のプロット

解の表面プロットを作成します。

surf(x,t,u)
title('Numerical solution computed with 20 mesh points')
xlabel('Distance x')
ylabel('Time t')

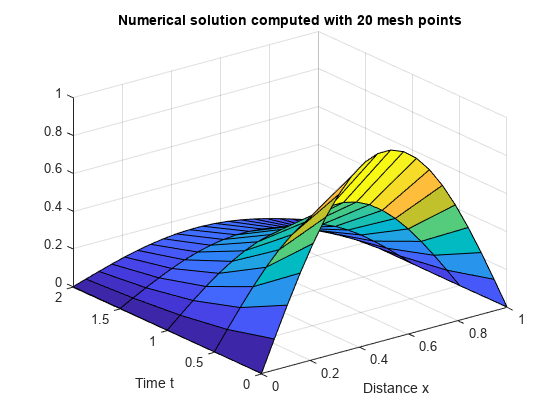
この問題の初期条件と境界条件は、次で与えられる解析解となるように選択されました。

$u (x, t) = e^{- t} \sin (π x) .$

同じメッシュ点で解析解をプロットします。

surf(x,t,exp(-t)'*sin(pi*x))
title('True solution plotted with 20 mesh points')
xlabel('Distance x')
ylabel('Time t')

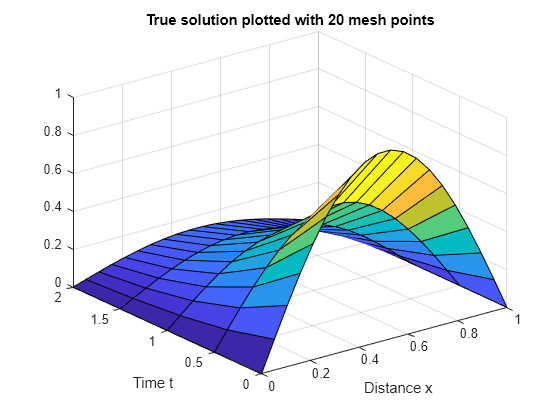
次に、数値解と解析解を $t$ の最終値である $t_{f}$ において比較します。この例では、 $t_{f} = 2$ となります。

plot(x,u(end,:),'o',x,exp(-t(end))*sin(pi*x))
title('Solution at t = 2')
legend('Numerical, 20 mesh points','Analytical','Location','South')
xlabel('Distance x')
ylabel('u(x,2)')

ローカル関数

ここでは、PDE ソルバー pdepe が解を計算するために呼び出すローカル補助関数を紹介しています。あるいは、これらの関数を独自のファイルとして MATLAB パスのディレクトリに保存することもできます。

function [c,f,s] = pdex1pde(x,t,u,dudx) % Equation to solve
c = pi^2;
f = dudx;
s = 0;
end
%----------------------------------------------
function u0 = pdex1ic(x) % Initial conditions
u0 = sin(pi*x);
end
%----------------------------------------------
function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t) % Boundary conditions
pl = ul;
ql = 0;
pr = pi * exp(-t);
qr = 1;
end
%----------------------------------------------

参考

pdepe