このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
regionprops
イメージ領域のプロパティの計測
構文
説明
関数 regionprops は、イメージ内の各オブジェクト (連結要素) のプロパティ (面積、重心、境界ボックスなど) を測定します。regionprops は連続領域と不連続領域の両方をサポートします。
regionprops は、2 次元イメージには 8 連結近傍を、それより高次元のイメージには最大連結を使用して、バイナリ イメージ内の固有オブジェクトを検出します。詳細については、ピクセルの連結性を参照してください。その他の種類の連結性を使用してオブジェクトを検出するには、代わりに bwconncomp を使用して連結要素を作成し、次に CC 引数を使用してその結果を regionprops に渡します。
メモ
3-D ボリューム イメージ内のオブジェクトのプロパティを測定するには、代わりに regionprops3 を使用することを検討してください。regionprops は 3-D イメージを受け入れることができますが、regionprops3 の方が 3-D イメージの多くの統計値をサポートしています。
関数 regionprops を呼び出す際は、properties 引数を省略できます。この場合、関数は "Area"、"Centroid"、および "BoundingBox" の測定値を返します。
stats = regionprops(BW,properties)BW 内の各オブジェクトのプロパティを測定します。
stats = regionprops(CC,properties)bwconncomp によって返される構造体である CC 内の各連結要素のプロパティを測定します。
stats = regionprops(L,properties)L にある各ラベル付き領域のプロパティを測定します。
stats = regionprops(outputFormat,___)outputFormat 引数を使用して、返される測定値の形式を構造体の配列またはテーブルとして指定します。
例
重心の計算とイメージとの重ね合わせ
バイナリ イメージをワークスペースに読み取ります。
BW = imread('text.png');regionprops を使用してイメージ内の連結要素の重心を計算します。関数 regionprops は重心を構造体配列で返します。
s = regionprops(BW,'centroid');重心の x 座標と y 座標を 2 列の行列に格納します。
centroids = cat(1,s.Centroid);
重心の位置を重ね合わせたバイナリ イメージを表示します。
imshow(BW) hold on plot(centroids(:,1),centroids(:,2),'b*') hold off

円形オブジェクトの中心と半径の推定と円のプロット
イメージ内の円形オブジェクトの中心と半径を推定し、この情報を使用して円をイメージ上にプロットします。この例では、regionprops は測定した領域プロパティを table で返します。
イメージをワークスペースに読み取ります。
a = imread("circlesBrightDark.png");入力イメージをバイナリ イメージに変換します。
bw = a < 50;
imshow(bw)
title("Image with Circles")
イメージ内の領域のプロパティを計算し、データをテーブルで返します。
stats = regionprops("table",bw,"Centroid", ... "MajorAxisLength","MinorAxisLength")
stats=3×3 table
Centroid MajorAxisLength MinorAxisLength
________________ _______________ _______________
300 120 79.517 79.517
330.29 369.92 109.49 108.6
450 240 99.465 99.465
円の中心と半径を取得します。
centers = stats.Centroid; diameters = mean([stats.MajorAxisLength stats.MinorAxisLength],2); radii = diameters/2;
円をプロットします。
hold on
viscircles(centers,radii)ans =
Group with properties:
Children: [2x1 Line]
Visible: on
HitTest: on
Use GET to show all properties
hold off
入力引数
BW — バイナリ イメージ
logical 配列
バイナリ イメージ。任意の次元の logical 配列として指定します。
regionprops は、各要素の top-left 極値を基準に、バイナリ イメージに含まれるオブジェクトを左から右に並べ替えます。複数のオブジェクトの水平位置が同じ場合、関数はそれらのオブジェクトを上から下に並べ替えた後、より高い次元に沿って再度並べ替えます。regionprops は、並べ替え後のオブジェクトと同じ順序で、測定されたプロパティ stats を返します。
データ型: logical
CC — 連結要素
構造体
連結要素。bwconncomp によって返される構造体として指定します。
データ型: struct
L — ラベル イメージ
数値配列 | categorical 配列
ラベル イメージ。次のいずれかとして指定します。
任意の次元の数値配列。
0とラベル付けされたピクセルは背景です。1とラベル付けされたピクセルは 1 番目のオブジェクトを構成し、2とラベル付けされたピクセルは 2 番目のオブジェクトを構成する、というように、次々にオブジェクトを構成します。regionpropsは負の値のピクセルを背景として扱い、整数でない入力ピクセルを丸めます。数値ラベル イメージは、watershedやlabelmatrixなどのラベル付け関数から取得できます。categorical 配列。各カテゴリが異なる領域に対応します。
データ型: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | categorical
properties — 測定のタイプ
"basic" (既定値) | string スカラーまたは文字ベクトルのコンマ区切りリスト | string スカラーの配列 | 文字ベクトルの cell 配列 | "all"
測定のタイプ。string スカラーもしくは文字ベクトルのコンマ区切りリスト、string スカラーの配列、文字ベクトルの cell 配列、または "all" もしくは "basic" のいずれかとして指定します。
"all"を指定すると、regionpropsはすべての形状測定値を計算し、グレースケール イメージを指定した場合は、ピクセル値の測定値も計算します。"basic"を指定すると、regionpropsは"Area"、"Centroid"および"BoundingBox"の測定値のみを計算します。
以下の表に、形状測定を提供するすべてのプロパティを示します。ピクセル値測定の表に示すプロパティは、グレースケール イメージを指定する場合のみ有効です。
形状測定
| プロパティ名 | 説明 | N 次元サポート | GPU サポート | コード生成 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
"Area" | 領域内の実際のピクセル数。スカラーとして返されます。この値は、ピクセル パターンの重み付け方法が異なる 3-D ボリュームの領域に相当するものを見つけるには、 | あり | あり | あり | ||||||||
"BoundingBox" | 領域を含む最小のボックスの位置とサイズ。1 行 (2*Q) 列のベクトルとして返されます。ここで、Q はイメージの次元です。最初の Q 個の要素は、ボックスの最小コーナーの座標です。2 番目の Q 個の要素は、各次元に沿ったボックスのサイズです。たとえば、値が | あり | あり | あり | ||||||||
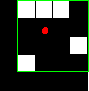
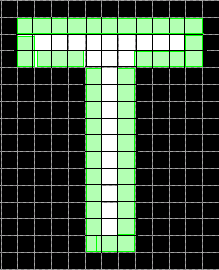
"Centroid" | 領域の重心。1 行 Q 列のベクトルとして返されます。ここで、Q はイメージの次元です。 この図は、「discontiguous」領域の重心と境界ボックスを示しています。領域は白いピクセルで構成されます。緑色のボックスは境界ボックス、赤い点は重心です。
| あり | あり | あり | ||||||||
"Circularity" | オブジェクトの丸さ。フィールド
最大真円度値は 1 です。入力は、ラベル行列または連続領域を持つバイナリ イメージでなければなりません。イメージに不連続領域が含まれている場合、 | 2 次元のみ | なし | あり | ||||||||
"ConvexArea" | ConvexImage 内のピクセル数。スカラーとして返されます。 | 2 次元のみ | なし | なし | ||||||||
"ConvexHull" | 領域を含むことができる最小の凸多角形。p 行 2 列の行列として返されます。行列の各行には、多角形の 1 頂点の x 座標と y 座標が含まれています。 | 2 次元のみ | なし | なし | ||||||||
"ConvexImage" | 凸包内のピクセルがすべて塗りつぶされた状態 (on に設定) の凸包を指定するイメージ。バイナリ イメージとして返されます。イメージは、領域の境界ボックスのサイズです。凸包の境界が通過するピクセルについては、regionprops はClassify Pixels That Are Partially Enclosed by ROIに記載されているアルゴリズムを使用します。 | 2 次元のみ | なし | なし | ||||||||
"Eccentricity" | 領域と同じ 2 次モーメントを持つ楕円の離心率。スカラーとして返されます。離心率とは、楕円の焦点間の距離と長軸の長さの割合です。この値は 0 ~ 1 になります (0 と 1 は変性した場合です。実際には、離心率が 0 の楕円は円で、離心率が 1 の楕円は線分です)。 | 2 次元のみ | あり | あり | ||||||||
"EquivDiameter" | 領域と同じ面積を持つ円の直径。スカラーとして返されます。sqrt(4*Area/pi) と同様に計算します。 | 2 次元のみ | あり | あり | ||||||||
"EulerNumber" | 領域内のオブジェクトの数からそれらのオブジェクトにある穴の数を差し引いた数。スカラーとして返されます。このプロパティは、2 次元ラベル行列のみでサポートされています。regionprops は 8 連結性を使用して、オイラー数 (オイラー標数とも呼ばれる) を計算します。詳細については、ピクセルの連結性を参照してください。 | 2 次元のみ | なし | あり | ||||||||
"Extent" | 境界ボックス全体のピクセル数に対する領域内ピクセル数の割合。スカラーとして返されます。境界ボックスの領域で除算された Area として計算されます。 | 2 次元のみ | あり | あり | ||||||||
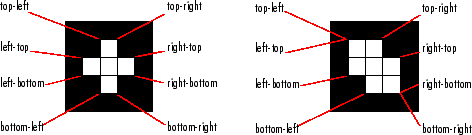
"Extrema" | 領域の極値点。8 行 2 列の行列として返されます。行列の各行には、1 点の x 座標と y 座標が含まれています。ベクトルの形式は この図は、2 つの異なる領域の極値を示しています。左側の領域では、各極値点は別々になります。右側の領域の場合、特定の極値点 (
| 2 次元のみ | あり | あり | ||||||||
"FilledArea" | FilledImage 内の on ピクセル数。スカラーとして返されます。 | あり | なし | あり | ||||||||
"FilledImage" | 領域の境界ボックスと同じサイズのイメージ。バイナリ配列として返されます。この図に示すように、
| あり | なし | あり | ||||||||
"Image" | 領域の境界ボックスと同じサイズのイメージ。バイナリ配列として返されます。on ピクセルは領域に対応しており、他のすべてのピクセルは off です。 | あり | あり | あり | ||||||||
"MajorAxisLength" | 領域と同じ正規化された 2 次中心モーメントを持つ楕円の長軸の長さ (ピクセル単位)。スカラーとして返されます。 | 2 次元のみ | あり | あり | ||||||||
"MaxFeretProperties" | 最大フェレ径、その相対角度、および座標値を含むフェレ プロパティ。以下のフィールドを含む構造体として返されます。
入力は、バイナリ イメージ、連結要素、またはラベル行列です。 | 2 次元のみ | なし | なし | ||||||||
"MinFeretProperties" | 最小フェレ径、その相対角度、および座標値を含むフェレ プロパティ。以下のフィールドを含む構造体として返されます。
入力は、バイナリ イメージ、連結要素、またはラベル行列です。 | 2 次元のみ | なし | なし | ||||||||
"MinorAxisLength" | 領域と同じ正規化された 2 次中心モーメントを持つ楕円の短軸の長さ (ピクセル単位)。スカラーとして返されます。 | 2 次元のみ | あり | あり | ||||||||
"Orientation" | x 軸と、領域と同じ 2 次モーメントを持つ楕円の長軸との角度。スカラーとして返されます。この値の単位は度で、範囲は -90 ~ 90 度になります。この図は、楕円の軸と方向を示しています。図の左側は、イメージ領域とその対応する楕円を示しています。右側は同じ楕円を示し、青の実線で軸を表しています。赤い点は焦点で、方向は水平の点線と長軸の角度になります。
| 2 次元のみ | あり | あり | ||||||||
"Perimeter" | 領域の境界の周囲長。スカラーとして返されます。
| 2 次元のみ | なし | あり | ||||||||
"PixelIdxList" | 領域内のピクセルの線形インデックス。p 要素ベクトルとして返されます。 | あり | あり | あり | ||||||||
"PixelList" | 領域内のピクセルの位置。p 行 Q 列の行列として返されます。行列の各行は [x y z ...] の形式で、領域内の 1 ピクセルの座標を指定します。 | あり | あり | あり | ||||||||
"Solidity" | 領域内にもある凸包のピクセルの比率。スカラーとして返されます。固体度は
| 2 次元のみ | なし | なし | ||||||||
"SubarrayIdx" | オブジェクト境界ボックスの内側にある L の要素。L(idx{:}) が要素を抽出するようなインデックスを含んでいる cell 配列として返されます。 | あり | あり | なし |
以下の表に示すピクセル値測定プロパティは、グレースケール イメージ I を指定する場合のみ有効です。
ピクセル値測定
| プロパティ名 | 説明 | N 次元サポート | GPU サポート | コード生成 |
|---|---|---|---|---|
"MaxIntensity" | 領域内で最大の強度を持つピクセルの値。スカラーとして返されます。 | あり | あり | あり |
"MeanIntensity" | 領域内のすべての強度値の平均。スカラーとして返されます。 | あり | あり | あり |
"MinIntensity" | 領域内で最小の強度を持つピクセルの値。スカラーとして返されます。 | あり | あり | あり |
"PixelValues" | 領域内のピクセル数。p 行 1 列のベクトルで返されます。ここで、p は領域内のピクセル数です。ベクトルの各要素には、領域内のピクセルの値が含まれています。 | あり | あり | あり |
"WeightedCentroid" | 位置と強度値に基づく領域の中心。座標の p 行 Q 列のベクトルとして返されます。WeightedCentroid の最初の要素は、重み付き重心の水平座標 (または x 座標) です。2 番目の要素は、垂直座標 (または y 座標) です。WeightedCentroid の他のすべての要素は、次元の順序になります。 | あり | あり | あり |
データ型: char | string | cell
outputFormat — 出力形式
"struct" (既定値) | "table"
測定値 stats の出力形式。次のいずれかの値として指定します。
| 値 | 説明 |
|---|---|
"struct" | BW、max( のオブジェクトの数と長さが等しい構造体の配列を返します。構造体配列のフィールドは、properties で指定されているように、各領域のさまざまなプロパティを示します。 |
"table" |
|
データ型: char | string
出力引数
stats — 測定値
struct 配列 (既定値) | table
測定値。構造体の配列またはテーブルとして返されます。配列の構造体の数またはテーブルの行数は、BW、CC.NumObjects または max(L(:)) のオブジェクトの数と等しくなります。各構造体のフィールドまたは各行の変数は、properties で指定された、各領域で計算されるプロパティを示します。入力イメージがカテゴリカル ラベル イメージ L の場合、stats は追加のフィールドまたは変数と "LabelName" プロパティを含みます。
stats に含まれる測定値の順序は、バイナリ イメージ BW に含まれる並べ替え後のオブジェクトと同じになるか、CC または L で指定された順序付きオブジェクトと同じになります。
詳細
連続領域と不連続領域
連続領域は、"オブジェクト"、"連結要素"、または"ブロブ" とも呼ばれます。連続領域を含んでいるラベル イメージ L は、次のように表示されることがあります。
1 1 0 2 2 0 3 3 1 1 0 2 2 0 3 3
1 に等しい L の要素は、最初の連続領域または連結要素に属します。2 に等しい L の要素は、2 番目の連結要素に属します。以下同様です。
不連続領域は、複数の連結要素を含んでいる可能性のある領域です。不連続領域を含んでいるラベル イメージは、次のように表示されることがあります。
1 1 0 1 1 0 2 2 1 1 0 1 1 0 2 2
L の要素は、2 つの連結要素を含んでいる最初の不連続領域に属します。2 に等しい L の要素は、1 つの連結要素である 2 番目の領域に属します。 ヒント
関数
ismemberは、特定の条件を満たすオブジェクトまたは領域のみを含んでいるバイナリ イメージの作成に役立ちます。たとえば、次のコマンドでは、面積が 80 より大きく、かつ離心率が 0.8 未満の領域のみを含んでいるバイナリ イメージが作成されます。cc = bwconncomp(BW); stats = regionprops(cc,"Area","Eccentricity"); idx = find([stats.Area] > 80 & [stats.Eccentricity] < 0.8); BW2 = ismember(labelmatrix(cc),idx);
regionpropsは、関連する測定の計算には中間結果を利用します。したがって、最も高速なのは、regionpropsを 1 回呼び出すだけで目的の計測をすべて計算することです。ほとんどの測定の計算には、短い時間しかかかりません。ただし、以下の測定には
Lの領域数によっては長い時間がかかる場合もあります。"ConvexHull""ConvexImage""ConvexArea""FilledImage"
拡張機能
C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。
使用上の注意および制限:
regionpropsでは C コードの生成がサポートされています (MATLAB® Coder™ が必要)。汎用のMATLAB Host Computerターゲット プラットフォームを選択した場合、プリコンパイルされたプラットフォーム固有の共有ライブラリを使用するコードが、regionpropsによって生成されます。共有ライブラリを使用するとパフォーマンスの最適化は維持されますが、コードを生成できるターゲット プラットフォームが限定されます。詳細については、Image Processing Toolbox でサポートされているコード生成のタイプを参照してください。バイナリ イメージと数値ラベル イメージのみがサポートされています。データ型 categorical の入力ラベル イメージはサポートされていません。
出力タイプ
"table"の指定はサポートされていません。cell 配列のプロパティを渡すことはサポートされていません。代わりに、コンマ区切りリストを使用します。
"ConvexArea"、"ConvexHull"、"ConvexImage"、"MaxFeretProperties"、"MinFeretProperties"、"Solidity"、"SubarrayIdx"以外のすべてのプロパティがサポートされています。
GPU コード生成
GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。
使用上の注意および制限:
GPU Coder™ は、バイナリ イメージに対してのみ、最適化された CUDA® コードを生成します。入力ラベル イメージに対して生成されたコードは最適化されません。データ型 categorical の入力ラベル イメージはサポートされていません。
出力タイプ
"table"の指定はサポートされていません。cell 配列のプロパティを渡すことはサポートされていません。代わりに、コンマ区切りリストを使用します。
"Area"、"BoundingBox"、"Centroid"、"Eccentricity"、"EquivDiameter"、"Extent"、"MajorAxisLength"、"MinorAxisLength"、"Orientation"、"PixelIdxList""PixelList"、"MaxIntensity"、"MeanIntensity"、"MinIntensity"、"PixelValues"、および"WeightedCentroid"のプロパティのみをサポートしています。
スレッドベースの環境
MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。
この関数は、スレッドベースの環境を完全にサポートします。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。
GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。
使用上の注意および制限:
gpuArray入力は、2 次元 logical 行列または 2 次元ラベル行列でなければなりません。連結要素構造体 (
CC) の入力はサポートされていません。"ConvexArea"、"ConvexHull"、"ConvexImage"、"Circularity"、"EulerNumber"、"FilledArea"、"FilledImage"、"MaxFeretProperties"、"MinFeretProperties"、および"Solidity"プロパティはサポートされていません。サポートされている戻り値の型は
"struct"のみです。
詳細については、GPU でのイメージ処理を参照してください。
バージョン履歴
R2006a より前に導入R2023a: 新しい真円度方程式
関数 regionprops は、新しい方程式を使用して真円度を計算します。この新しい方程式では、比較的小さなオブジェクトについて計算された真円度が高くなりすぎる原因となったバイアスが解消されています。
以前の方程式を使用した真円度の測定値を再現する場合は、次のコマンドを使用してください。
props = regionprops(I,["Area" "Perimeter"]); oldCircularity = 4*pi*props.Area ./ props.Perimeter.^2;
R2022b: スレッドベース環境のサポート
regionprops は、スレッドベースの環境をサポートするようになりました。
R2022a: regionprops は Image、ConvexImage、および FilledImage のプロパティをすべての入力の出力テーブル内の cell 配列 として格納
R2022a 以降では、テーブル出力形式が指定された場合、image オブジェクトのサイズに関係なく、関数 regionprops は Image、ConvexImage、および FilledImage のプロパティ値を cell 配列として格納します。以前のリリースでは、オブジェクトの境界ボックスのサイズが 1 × 1 または 1 × "n" の場合、これらのプロパティは数値スカラーまたは行ベクトルとして出力テーブル内に格納されました。
コードを更新するには、中かっこ {} で囲むドット表記を使用して、Image、ConvexImage、および FilledImage のプロパティの値にアクセスします。たとえば、以下のコードを使用して、入力イメージ BW 内の最初のオブジェクトの Image プロパティにアクセスします。以前のリリースでは、数値スカラーまたは行ベクトルとして格納された値へのアクセスに、中かっこは必要ありませんでした。
stats = regionprops("table",BW,"Image"); imdata = stats.Image{1};
R2020a: categorical データのサポート
regionprops は categorical イメージ データをサポートするようになりました。
R2019a: 新しい真円度およびフェレ プロパティ
regionprops は、バイナリ イメージ内の領域の真円度およびフェレ プロパティを測定するようになりました。真円度、最小フェレ プロパティ、または最大フェレ プロパティを測定するには、properties 引数の指定時にそれぞれ "Circularity"、"MinFeretProperties"、または "MaxFeretProperties" を含めます。
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)