ピクセルの連結性

"ピクセルの連結性" は、各ピクセルが、他のどのピクセルと連結するかを定義します。バイナリイメージ内の連結する一連の前景ピクセルは "オブジェクト" または "連結要素" と呼ばれます。

次の表は、ツールボックスでサポートしている標準的な 2 次元と 3 次元の連結性をすべて示しています。

値	平均
2 次元連結性
`4`	ピクセルのエッジの部分が接触している場合、ピクセルは連結されます。2 つの隣り合ったピクセルは両方とも "on" の場合に同じオブジェクトの一部であり、水平方向または垂直方向に連結します。	現在のピクセルを灰色で示します。
`8`	ピクセルのエッジまたはコーナーが接触している場合、ピクセルは連結されます。2 つの隣り合ったピクセルは両方とも "on" の場合に同じオブジェクトの一部であり、水平方向、垂直方向または対角方向に連結します。	現在のピクセルを灰色で示します。
3 次元連結性
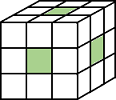
`6`	面が接触している場合、ピクセルは連結されます。2 つの隣り合ったピクセルは両方とも "on" の場合に同じオブジェクトの一部であり、次のように連結します。次のいずれかの方向: 奥、手前、左、右、上および下	現在のピクセルは立方体の中心です。
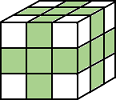
`18`	面またはエッジが接触している場合、ピクセルは連結されます。2 つの隣り合ったピクセルは両方とも "on" の場合に同じオブジェクトの一部であり、次のように連結します。次のいずれかの方向: 奥、手前、左、右、上および下右下または上の奥など、2 つの方向の組み合わせ	現在のピクセルは立方体の中心です。
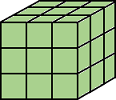
`26`	面、エッジまたはコーナーが接触している場合、ピクセルは連結されます。2 つの隣り合ったピクセルは両方とも "on" の場合に同じオブジェクトの一部であり、次のように連結します。次のいずれかの方向: 奥、手前、左、右、上および下右下または上の奥など、2 つの方向の組み合わせ右上の奥または左下の奥など、3 つの方向の組み合わせ	現在のピクセルは立方体の中心です。

連結性の選択

ユーザーが選択した近傍のタイプは、イメージの中で検出されるオブジェクトの数やそのオブジェクトの境界に影響します。このために、多くのモルフォロジー演算の結果は、ユーザーが指定した連結性のタイプによって異なる可能性があります。

たとえば、4 連結近傍を指定した場合、次のバイナリイメージに含まれるオブジェクトは 2 つです。8 連結近傍を指定した場合は、イメージに含まれるオブジェクトは 1 つだけとなります。

0     0     0     0     0     0
0     1     1     0     0     0
0     1     1     0     0     0
0     0     0     1     1     0
0     0     0     1     1     0

カスタム連結性の定義

また、0 と 1 の 3 x 3 x ... x 3 の配列を指定して、カスタム近傍を定義することもできます。値 1 を持つ要素は、中心要素を基準に近傍の連結性を定義します。

たとえば、次の配列は "North/South" 連結性を定義し、独立した列にイメージを分解する効果をもっています。

CONN = [ 0 1 0; 0 1 0; 0 1 0 ]

CONN =
     0     1     0
     0     1     0
     0     1     0

メモ

連結性配列は、その中心要素に対して対称でなければなりません。また、3 次元イメージに 2 次元連結性配列を使用することができます。つまり、連結性は 3 次元イメージの各平面に影響します。

参考