モルフォロジー再構成
モルフォロジー再構成を使用して、マークされたオブジェクトをイメージから抽出したり、強調したりすることができます。強調したいイメージを "マスク イメージ" と呼びます。それとは別に、抽出や強調を行う領域をマークするために使用するイメージを "マーカー イメージ" と呼びます。マーカー イメージのピークは、マスク イメージを塗りつぶすように広がるシード ピクセルとして機能します。概念的には、このプロセスは、マーカー イメージの繰り返し膨張と考えることができます。
メモ
モルフォロジー再構成がツールボックスでどのように実装されているのかを学ぶには、imreconstruct を参照してください。
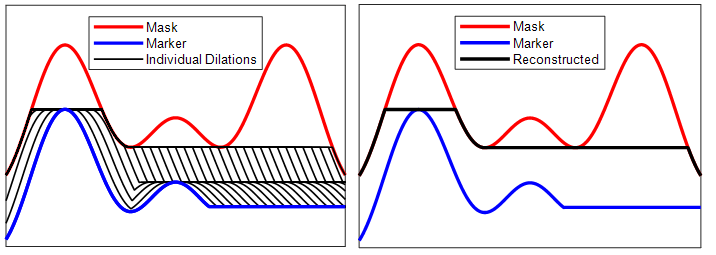
以下の図はこの概念を 1 次元で示しています。個々の連続的な膨張はマスクの下に拘束されます。最後の膨張は再構成されたイメージです
マスクに拘束されたマーカー イメージの繰り返し膨張

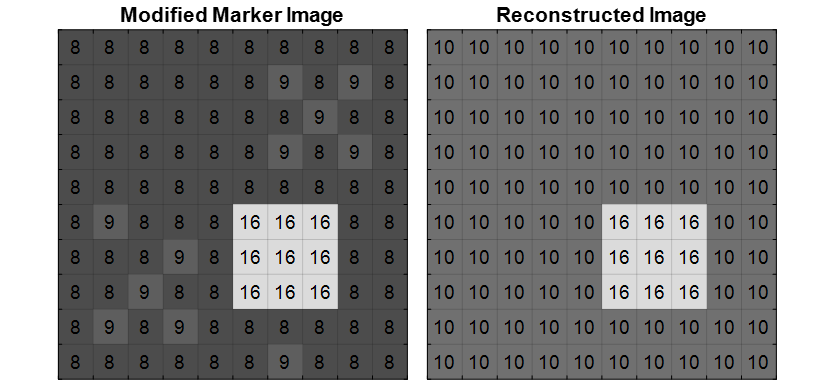
マーカー イメージを変更すると、再構築されるイメージは変わります。以下の図では、マーカー イメージ内の最も右にあるピークが抑えられています。このため、再構築されたイメージではこのピークがなくなっています。
変更したマーカー イメージによるモルフォロジー再構成
モルフォロジー再構成はモルフォロジー膨張に基づいていますが、異なる特性として次のような点があります。
処理は、1 つのイメージと構造化要素ではなく、マーカーとマスクという 2 つのイメージを使用します。
モルフォロジー再構成は、特定の形状とサイズをもつ構造化要素ではなく、ピクセルの連結性を使用するので、このプロセスではマスク イメージ内のオブジェクトの形状とサイズが維持されます。ピクセルの連結性の詳細については、ピクセルの連結性を参照してください。
処理は、イメージの値が変化しなくなるまで続行されます。
モルフォロジー再構成では、マーカー イメージとピクセル連結性を変更することによって演算結果を制御できます。
マーカー イメージとマスク イメージ
2 次元のグレースケール マスク イメージを考えてみます。このイメージには 2 つの主な領域 (強度値 14 と 18 を含むピクセルの集合として表される) があります。背景ピクセルのほとんどの強度値は 10 ですが、いくつかの値は 11 です。

このイメージをモルフォロジーに再構成するには、以下の手順に従います。
マーカー イメージを作成します。膨張と収縮での構造化要素と同様に、モルフォロジー再構成ではマーカー イメージの特性によって実行される処理が決定します。マーカー イメージ内のピークは、強調するマスク イメージ内のオブジェクトの位置を識別できるものでなくてはなりません。
マーカー イメージを作成する方法の 1 つに、マスク イメージの各ピクセルから定数を差し引くという方法があります。この例では、マスク イメージの各ピクセルから
2を差し引いてマーカー イメージを作成しています。
関数
imreconstructを使用して、イメージをモルフォロジーに再構成します。次のアニメーションは、イメージの値が徐々に増大する変化を示しています。各手順において、マーカー イメージは膨張されますが、各ピクセルの値が、マスク イメージ内の該当する値を超えることはありません。

最終的に再構築されたイメージでは、強度の小さい変更が取り除かれています。周辺のピクセルより値が 2 以上大きいピークのみが残っています。この差のしきい値は、マーカー イメージを作成するためにマスク イメージから差し引いた値に一致します。モルフォロジー再構成を使用してグレースケール イメージ内のピークを変更する場合の詳細については、Suppress Minima and Maximaを参照してください。

マーカー イメージを変更すると、再構築されるイメージは変わります。左上のピーク内のピクセルの値を、背景に合わせて 12 から 8 に変更することによって、マーカー イメージからピークの 1 つを取り除きます。新たに再構築されたイメージは、マーカー イメージ内のピークに該当する場所に 1 つだけピークをもちます。
次のアニメーションは、変更したマーカー イメージによってイメージの値が徐々に増大する変化を示しています。

ピクセルの連結性による影響
モルフォロジー再構成では、マーカー イメージ内のピークが徐々に近傍のピクセルに広がっていきます。指定するピクセル連結性によって、近傍の境界が決まります。
斜め方向に隣接する 2 つの正方形をもつバイナリ イメージを考えてみます。8 連結の近傍 (関数 imreconstruct の既定値) に基づく場合、この 2 つの正方形は 1 つの前景オブジェクトとなります。4 連結の近傍に基づく場合は、2 つの前景オブジェクトとなります。

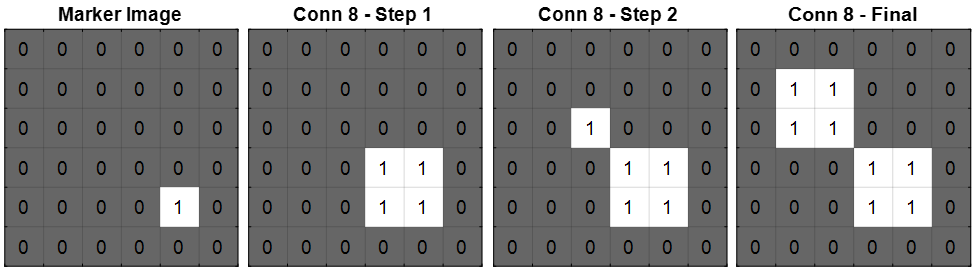
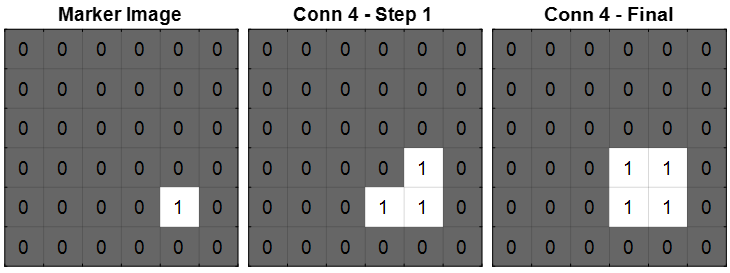
この例では、右下の正方形内に 1 ピクセルのピーク 1 つをもつマーカー イメージを使用してモルフォロジー再構成を実行します。これは、関数 bwselect が実行する演算に相当します。
8 連結の近傍を指定した場合、各手順で、マーカー イメージ内のピーク ピクセルはマスク イメージの値を限度として 8 連結のピクセルに膨張します。イメージの変化は、3 手順後に停止します。再構築された最終的なイメージには、マスク イメージにあった正方形が 2 つとも含まれます。
4 連結の近傍を指定してモルフォロジー再構成を実行すると、各手順で、マーカー イメージ内のピーク ピクセルはマスク イメージの値を限度として 4 連結のピクセルに膨張します。イメージの変化は、2 手順後に停止します。再構築された最終的なイメージには、マスク イメージの右下にあった正方形だけが含まれます。
次のアニメーションは、8 連結と 4 連結のバイナリ イメージにおいて徐々に増大する変化を示しています。

モルフォロジー再構成の応用
関数 imreconstruct を使用して一般的なモルフォロジー再構成を実行することにより、マスク イメージ内の領域の抽出、強調、抑制を行うことができます。また Image Processing Toolbox™ には、特殊なモルフォロジー再構成アルゴリズムを使用して特定のイメージ処理タスクを実現する関数も含まれています。
関数
imfillは暗い領域を抑制することによって、穴を塗りつぶしたり、塗りつぶし操作を実行したりします。詳細については、塗りつぶし操作を参照してください。関数
imclearborderは、イメージ境界に連結された明るい領域を抑制します。これは、イメージのエッジで一部が削除されているオブジェクトを取り除く場合に便利です。同様に、関数imkeepborderは、イメージ境界に連結された明るい領域を保持し、残りの領域を抑制します。関数
imextendedmax、imextendedmin、imhmax、imhmin、imimposeminは、特定の局所的な最小値および最大値を強調または抑制します。詳細については、Find Image Peaks and Valleysを参照してください。