このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

fwind1

1 次元ウィンドウ法を使用する 2 次元 FIR フィルター

構文

h = fwind1(Hd,win)

h = fwind1(Hd,win1,win2)

h = fwind1(f1,f2,Hd,___)

説明

関数 fwind1 はウィンドウ法を使用して 2 次元 FIR フィルターを設計します。fwind1 は 1 次元ウィンドウ仕様を使用して、目的の周波数応答に基づく 2 次元 FIR フィルターを設計します。fwind1 は 1 次元ウィンドウのみで機能します。2 次元ウィンドウで機能させるには、fwind2 を使用します。

関数 filter2 を使用して 2 次元 FIR フィルターをイメージに適用できます。

h = fwind1(Hd,win) は目的の周波数応答 Hd に基づく 2 次元 FIR フィルター h を作成します。関数 fwind1 は 1 次元ウィンドウ win を使用して、Huang 法でほぼ円対称な 2 次元ウィンドウを作成します。

h = fwind1(Hd,win1,win2) では 2 つの 1 次元ウィンドウ win1 と win2 を使用して分離可能な 2 次元ウィンドウを作成します。

h = fwind1(f1,f2,Hd,___) では目的とする周波数応答 Hd を x 軸と y 軸に沿って任意の周波数 f1 と f2 で指定することができます。

例

1 次元ウィンドウ法を使用する 2 次元 FIR フィルターの作成

この例では、1 次元ウィンドウ法を使用して、ほぼ円対称な 2 次元バンドパス フィルターを設計する方法を説明します。

freqspace を使用して、周波数範囲ベクトル f1 および f2 を作成します。これらのベクトルの長さは 21 です。

[f1,f2] = freqspace(21,'meshgrid');

中心周波数から各位置までの距離を計算します。

r = sqrt(f1.^2 + f2.^2);

目的とするバンドパス応答を格納する行列 Hd を作成します。この例で目的とする通過帯域は 0.1 ～ 0.5 (正規化周波数。ここで、1.0 はサンプリング周波数の 1/2 つまり $$\pi$$ ラジアンに相当します) です。

Hd = ones(21); 
Hd((r<0.1)|(r>0.5)) = 0;

理想的なバンドパス応答を表示します。

colormap(parula(64))
mesh(f1,f2,Hd)

1 次元ウィンドウを設計します。この例では、長さ 21 のハミング ウィンドウを使用します。

win = 0.54 - 0.46*cos(2*pi*(0:20)/20);

1 次元ウィンドウをプロットします。

figure
plot(linspace(-1,1,21),win);

1 次元ウィンドウを使用して、この周波数応答を最適に引き出すフィルターを設計します。

h = fwind1(Hd,win);

このフィルターの実際の周波数応答を表示します。

freqz2(h)

入力引数

Hd — 目的の周波数応答

数値行列

目的の周波数応答。数値行列として指定します。Hd は周波数軸 x と y に沿って正規化された周波数で -1.0 ～ 1.0 に等間隔に配置された点でサンプリングされた目的の周波数応答を格納する行列です。ここで、1.0 はサンプリング周波数の 1/2 つまり π ラジアンに相当します。結果の精度を上げるには、関数 freqspace を使用して Hd を作成します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

win — 1 次元ウィンドウ

数値行列

1 次元ウィンドウ。数値行列として指定します。Signal Processing Toolbox™ ソフトウェアがある場合は、ウィンドウとして hamming (Signal Processing Toolbox)、hann (Signal Processing Toolbox)、bartlett (Signal Processing Toolbox)、blackman (Signal Processing Toolbox)、kaiser (Signal Processing Toolbox)、chebwin (Signal Processing Toolbox) などを使用して win を指定できます。

データ型: single | double

win1 — 1 次元ウィンドウ

数値行列

1 次元ウィンドウ。数値行列として指定します。

データ型: single | double

win2 — 1 次元ウィンドウ

数値行列

1 次元ウィンドウ。数値行列として指定します。

データ型: single | double

f1 — x 軸上の目的の周波数

ベクトル

x 軸上の目的の周波数。周波数ベクトルは [-1, 1] の範囲でなければなりません。ここで、1.0 はサンプリング周波数の 1/2 つまり π ラジアンに相当します。

データ型: single | double

f2 — y 軸上の目的の周波数

ベクトル

y 軸上の目的の周波数。周波数ベクトルは [-1, 1] の範囲でなければなりません。ここで、1.0 はサンプリング周波数の 1/2 つまり π ラジアンに相当します。

データ型: single | double

出力引数

h — 2 次元 FIR フィルター

数値行列

2 次元 FIR フィルター。数値行列として返されます。ウィンドウの長さは結果として得られるフィルターのサイズを制御します。

• 1 つのウィンドウ win を指定し、長さが n の場合、h のサイズは n 行 n 列になります。

• 2 つのウィンドウ win1 と win2 を指定し、長さがそれぞれ n と m の場合、h のサイズは m 行 n 列になります。

Hd がデータ型 single の場合、h のデータ型は single です。それ以外の場合、h のデータ型は double です。

データ型: single | double

アルゴリズム

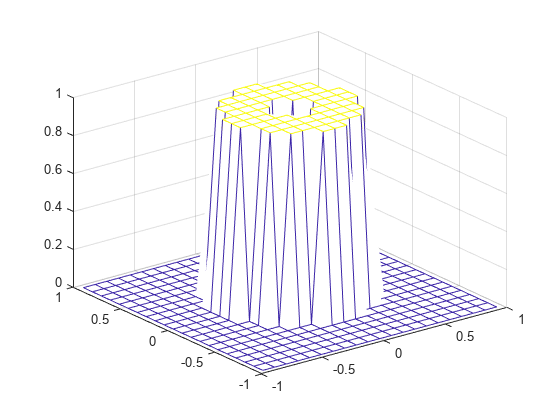
関数 fwind1 は 1 次元ウィンドウ仕様を使用して Huang 法を使用するほぼ円対称な 2 次元ウィンドウを形成します。

$$w(n_1,n_2)={w(t)|}_{t=\sqrt{n_{{}_1}^2+n_2^2}},$$

ここで、w(t) は 1 次元ウィンドウ、w(n₁,n₂) は結果として得られる 2 次元ウィンドウです。

2 つのウィンドウが与えられると、関数 fwind1 は分離可能な 2 次元ウィンドウを形成します。

$$w(n_1,n_2)=w_1(n_1)w_2(n_2).$$

関数 fwind1 は、目的の周波数応答 Hd と 2 次元ウィンドウをもつ fwind2 を呼び出します。関数 fwind2 は逆フーリエ変換と 2 次元ウィンドウによる乗算を使用して h を計算します。

$$h_d(n_1,n_2)=\frac{1}{{\left(2\pi \right)}^2}{\displaystyle {\int }_{-\pi }^{\pi }{\displaystyle {\int }_{-\pi }^{\pi }{H}_d({\omega }_1,{\omega }_2)e^{j{\omega }_1{n}_1}{e}^{j{\omega }_2{n}_2}d{\omega }_{1}d{\omega }_2}}$$

$$h(n_1,n_2)=h_d(n_1,n_2)w(n_1,n_2)$$

参照

[1] Lim, Jae S., Two-Dimensional Signal and Image Processing, Englewood Cliffs, NJ, Prentice Hall, 1990.

バージョン履歴

R2006a より前に導入

参考

conv2 | filter2 | fsamp2 | freqspace | ftrans2 | fwind2

トピック

• 周波数領域での線形フィルターの設計