このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

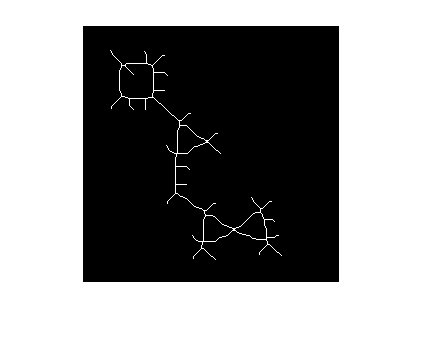
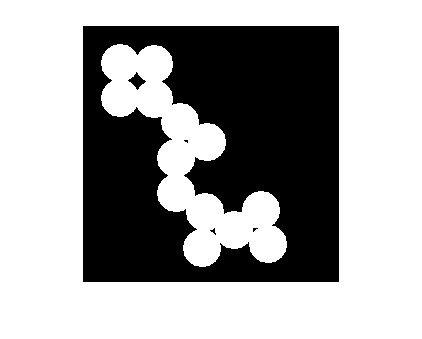bwmorph

バイナリ イメージのモルフォロジー演算

構文

BW2 = bwmorph(BW,operation)

BW2 = bwmorph(BW,operation,n)

説明

BW2 = bwmorph(BW,operation) は、特定のモルフォロジー演算をバイナリ イメージ BW に適用します。

メモ

3 次元ボリューム イメージのモルフォロジー演算を実行するには、bwmorph3 を使用します。

BW2 = bwmorph(BW,operation,n) は、演算を n 回適用します。n には Inf を使用できますが、その場合にはイメージが変更されなくなるまで処理が繰り返されます。

例

バイナリ イメージのモルフォロジー演算の実行

バイナリ イメージの読み取りと表示

BW = imread('circles.png');
imshow(BW);

内部のピクセルを削除して形状の輪郭を残します。

BW2 = bwmorph(BW,'remove');
figure
imshow(BW2)

イメージのスケルトンを取得します。

BW3 = bwmorph(BW,'skel',Inf);
figure
imshow(BW3)

入力引数

BW — バイナリ イメージ

2 次元数値行列 | 2 次元 logical 行列

バイナリ イメージ。2 次元数値行列または 2 次元 logical 行列として指定します。数値入力の場合、非ゼロのピクセルは 1 (true) であると見なされます。

operation — 実行するモルフォロジー演算

文字ベクトル | string スカラー

実行するモルフォロジー演算。以下のいずれかに指定します。

操作	説明
"bothat"	ボトム ハットを使用したモルフォロジー演算を実行し、そのイメージからイメージのモルフォロジー クロージングを差し引いたものを返します。 関数 bwmorph は、近傍の ones(3) を使用してモルフォロジー クロージングを実行します。異なる近傍でボトム ハットを使用したモルフォロジー演算を実行する場合は、関数 imbothat を使用します。
"branchpoints"	スケルトンの分岐点を検出する。次に例を示します。 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 1 1 1 becomes 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 メモ: 分岐点を見つけるには、イメージをスケルトン化しなければなりません。スケルトン化されたイメージを作成するには、bwmorph(BW,"skel") を使用します。
"bridge"	連結していない 2 つの非ゼロ近傍をもつ場合、連結されていないピクセルの橋渡しをする、つまり、0 の値をとるピクセルを 1 に設定します。次に例を示します。 1 0 0 1 1 0 1 0 1 becomes 1 1 1 0 0 1 0 1 1
"clean"	このパターンの中心ピクセルのように孤立したピクセル (0 に囲まれた単独の 1) を削除します。 0 0 0 0 1 0 0 0 0
"close"	モルフォロジー クロージング (膨張の後に収縮) を実行します。 関数 bwmorph は、近傍の ones(3) を使用してモルフォロジー クロージングを実行します。異なる近傍でモルフォロジー クロージング演算を実行する場合は、関数 imclose を使用します。
"diag"	対角の塗りつぶしを使用して、背景の 8 連結性を削除します。次に例を示します。 0 1 0 0 1 0 1 0 0 becomes 1 1 0 0 0 0 0 0 0
"endpoints"	スケルトンの終点を検出します。次に例を示します。 1 0 0 0 1 0 0 0 0 1 0 0 becomes 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 メモ: 終点を見つけるには、イメージをスケルトン化しなければなりません。スケルトン化されたイメージを作成するには、bwmorph(BW,"skel") を使用します。
"fill"	このパターンの中心ピクセルのように孤立した内部ピクセル (1 に囲まれた単独の 0) を塗りつぶします。 1 1 1 1 0 1 1 1 1
"hbreak"	H 連結ピクセルを削除します。次に例を示します。 1 1 1 1 1 1 0 1 0 becomes 0 0 0 1 1 1 1 1 1
"majority"	3 行 3 列近傍内の 5 つ以上のピクセルが 1 の場合、ピクセルを 1 に設定します。そうでない場合は、ピクセルを 0 に設定します。
"open"	モルフォロジー オープニング (収縮の後に膨張) を実行します。 関数 bwmorph は、近傍の ones(3) を使用してモルフォロジー オープニングを実行します。異なる近傍でモルフォロジー オープニング演算を実行する場合は、関数 imopen を使用します。
"remove"	内部のピクセルを削除します。このオプションでは、すべての 4 連結近傍が 1 の場合にピクセルが 0 に設定されます。こうして、境界のピクセルのみが残されます。
"shrink"	n = Inf を使用し、オブジェクトの境界からピクセルを削除してオブジェクトを点に縮小します。穴のないオブジェクトは点に縮小され、穴のあるオブジェクトは各穴と外側の境界の中間で連結リングにまで縮小されます。このオプションでは、オイラー数 (オイラー標数とも呼ばれる) が保存されます。
"skel"	n = Inf を使用して、オブジェクトを壊さずにオブジェクトの境界上のピクセルを削除します。イメージのスケルトンは、残りのピクセルにより構成されます。このオプションでは、オイラー数が保存されます。 3 次元ボリュームを処理する、またはスケルトンを枝刈りするとき、関数 bwskel を使用します。
"spur"	枝分かれしたピクセルを削除します。次に例を示します。 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 becomes 0 0 0 0 0 1 0 0 0 1 0 0 1 1 0 0 1 1 0 0
"thicken"	n = Inf を使用して、連結されていないオブジェクトが 8 連結になるまでピクセルをオブジェクトの外部に追加することにより、オブジェクトを太くします。このオプションでは、オイラー数が保存されます。
"thin"	n = Inf を使用し、オブジェクトの境界からピクセルを削除して、線になるまでオブジェクトを細くします。穴のないオブジェクトは最小限に連結されたひと筆に縮小され、穴のあるオブジェクトは各穴と外側の境界の中間で連結リングにまで縮小されます。このオプションでは、オイラー数が保存されます。詳細については、アルゴリズムを参照してください。
"tophat"	トップ ハットを使用したモルフォロジー演算を実行し、そのイメージからイメージのモルフォロジー オープニングを差し引いたものを返します。 関数 bwmorph は、近傍の ones(3) を使用してモルフォロジー オープニングを実行します。異なる近傍でトップ ハットを使用したモルフォロジー演算を実行する場合は、関数 imtophat を使用します。

ヒント

モルフォロジー収縮またはモルフォロジー膨張を実行するには、それぞれ関数 imerode または imdilate を使用します。関数 bwmorph によって実行された収縮または膨張を繰り返す場合は、ones(3) として近傍を指定します。

データ型: char | string

n — 演算を実行する回数

正の整数 | Inf

演算を実行する回数。正の整数または Inf として指定します。n を Inf として指定した場合、イメージが変化しなくなるまで関数 bwmorph が演算を反復します。

例: 100

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

出力引数

BW2 — モルフォロジー演算後のイメージ

2 次元 logical 行列

モルフォロジー演算後のイメージ。2 次元 logical 行列として返されます。

データ型: logical

アルゴリズム

"thin" オプションと共に使用した場合、bwmorph は、次のアルゴリズム[3]を使用します。

1. 最初の部分反復では、条件 G₁、G₂、G₃ がすべて満たされる場合にのみ、ピクセル p を削除します。

2. 2 番目の部分反復では、条件 G₁、G₂、$$G_3\prime$$ がすべて満たされる場合にのみ、ピクセル p を削除します。

条件 G1 は次のとおりです。

$$X_H(p)=1$$

ここで、

$$X_H(p)={\displaystyle \sum _{i=1}^4{b}_i}$$

$$b_i=\{\begin{array}{c}1,\text{ if }{x}_{2i-1}=0\text{ and }(x_{2i}=1\text{ or }{x}_{2i+1}=1)\\ 0\text{, otherwise }\end{array}$$

x₁、x₂、...、x₈ は、p の 8 つの近傍の値です。東近傍から反時計回りに番号が振られています。

条件 G2 は次のとおりです。

$$2\le \min \left\{n_1(p),n_2(p)\right\}\le 3$$

ここで、

$$n_1(p)={\displaystyle \sum _{k=1}^4{x}_{2k-1}\vee x_{2k}}$$

$$n_2(p)={\displaystyle \sum _{k=1}^4{x}_{2k}\vee x_{2k+1}}$$

条件 G3 は次のとおりです。

$$(x_2\vee x_3\vee {\overline{x}}_8)\wedge x_1=0$$

条件 G3' は次のとおりです。

$$(x_6\vee x_7\vee {\overline{x}}_4)\wedge x_5=0$$

細線化アルゴリズムの反復作業 1 回分は、部分反復作業 2 回分で構成されています。反復回数 (n=Inf) として無限数を指定すると、イメージが変更しなくなるまで反復が行われます。条件はすべて、事前に計算されたルックアップ テーブルをもつ applylut を使用してテストされます。

参照

[1] Haralick, Robert M., and Linda G. Shapiro, Computer and Robot Vision, Vol. 1, Addison-Wesley, 1992.

[2] Kong, T. Yung and Azriel Rosenfeld, Topological Algorithms for Digital Image Processing, Elsevier Science, Inc., 1996.

[3] Lam, L., Seong-Whan Lee, and Ching Y. Suen, "Thinning Methodologies-A Comprehensive Survey," IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol 14, No. 9, September 1992, page 879, bottom of first column through top of second column.

[4] Pratt, William K., Digital Image Processing, John Wiley & Sons, Inc., 1991.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• bwmorph では C コードの生成がサポートされています (MATLAB^® Coder™ が必要)。汎用の MATLAB Host Computer ターゲット プラットフォームを選択した場合、プリコンパイルされたプラットフォーム固有の共有ライブラリを使用するコードが、bwmorph によって生成されます。共有ライブラリを使用するとパフォーマンスの最適化は維持されますが、コードを生成できるターゲット プラットフォームが限定されます。詳細については、Image Processing Toolbox でサポートされているコード生成のタイプを参照してください。

• コードを生成する際、演算を指定する文字ベクトルまたは string スカラーはコンパイル時の定数でなければなりません。最良の結果を得るには、入力イメージのクラスが logical でなければなりません。

GPU コード生成

GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

使用上の注意および制限:

• コードを生成する際、演算を指定する文字ベクトルまたは string スカラーはコンパイル時の定数でなければなりません。最良の結果を得るには、入力イメージのクラスが logical でなければなりません。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細については、GPU でのイメージ処理を参照してください。

バージョン履歴

R2006a より前に導入

参考

bweuler | bwskel | bwmorph3 | imdilate | bwperim | imerode

トピック

• モルフォロジー演算のタイプ
• ピクセルの連結性