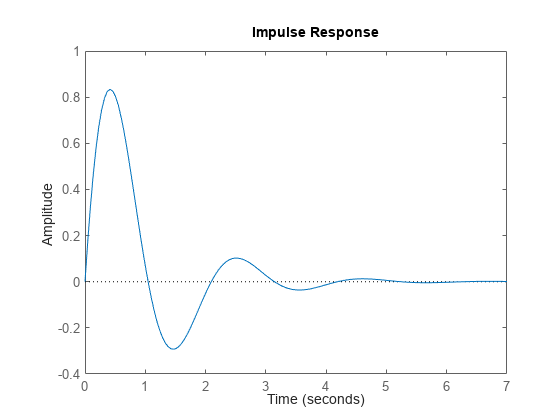
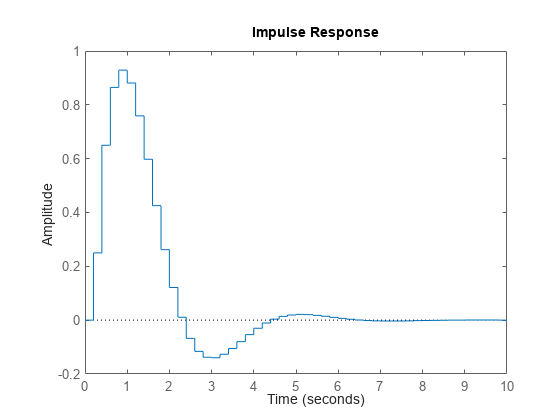
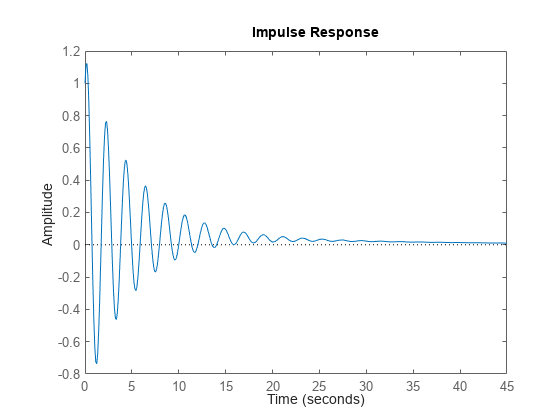
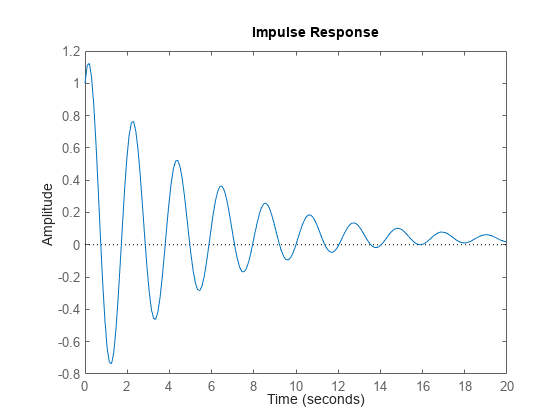
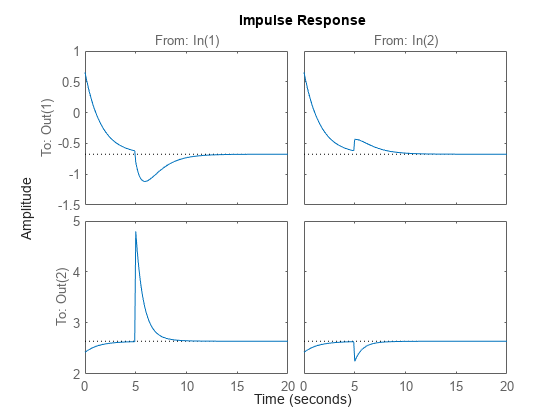
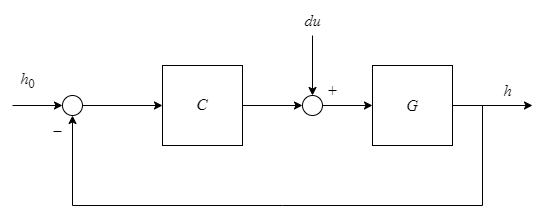
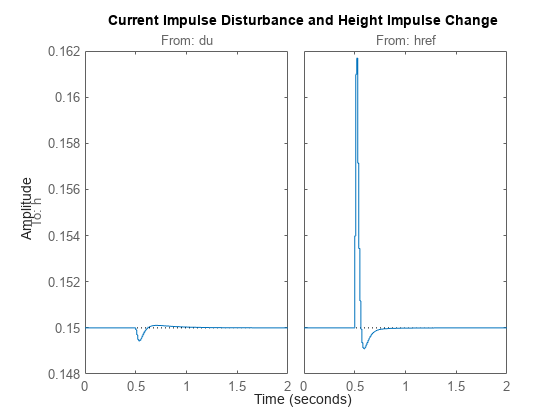
impulse
動的システムのインパルス応答プロット、インパルス応答データ
構文
説明
[ は、振幅や入力オフセットなど、インパルス応答を計算するための追加オプションを指定します。y,tOut] = impulse(___,config)RespConfig を使用して、オプション セット config を作成します。
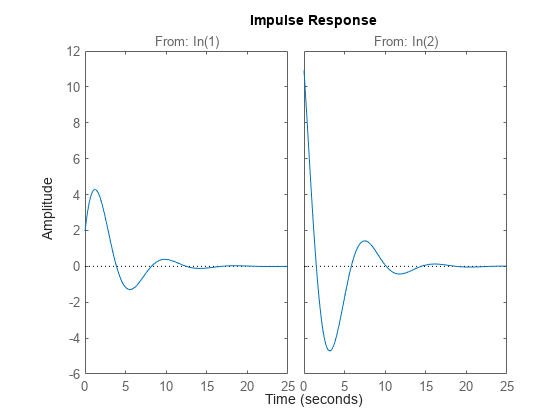
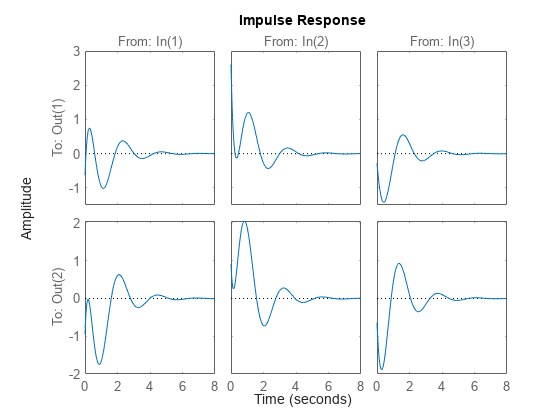
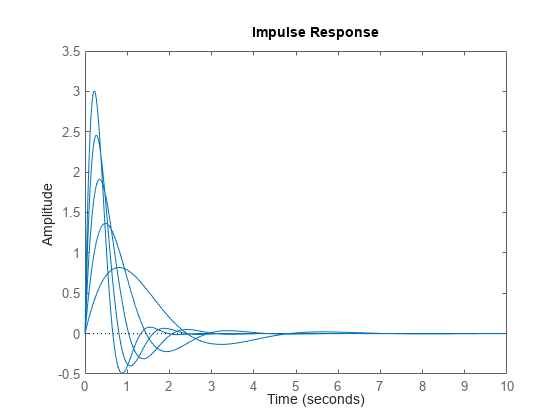
impulse(___) は、前述のすべての入力引数の組み合わせについて、sys のインパルス応答を既定のプロット オプションでプロットします。プロットをさらにカスタマイズするには、impulseplot を使用します。
複数の動的システムの応答を同じプロット上にプロットするには、
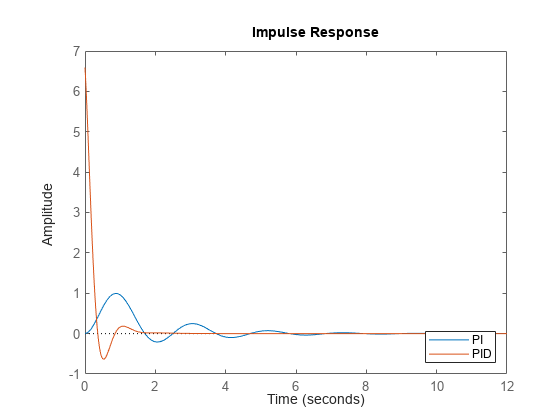
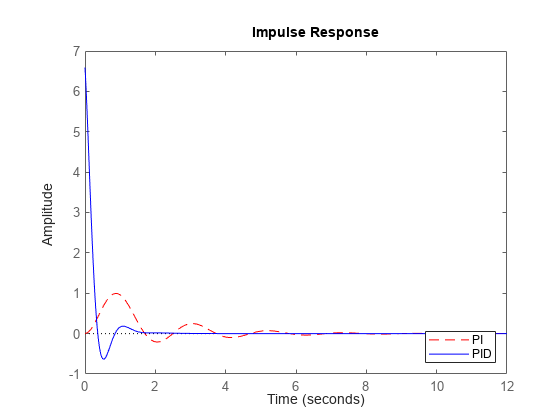
sysをモデルのコンマ区切りリストとして指定します。たとえば、impulse(sys1,sys2,sys3)は 3 つのモデルの応答を同じプロット上にプロットします。プロット内の各システムの色、ライン スタイル、およびマーカーを指定するには、システムごとに
LineSpec値を指定します。たとえば、impulse(sys1,LineSpec1,sys2,LineSpec2)は 2 つのモデルをプロットし、それらのプロット スタイルを指定します。LineSpec値の指定の詳細については、impulseplotを参照してください。
例
以下の伝達関数で表される連続時間システムのインパルス応答をプロットします。
この例では、伝達関数を表す tf モデルを作成します。零点-極-ゲイン (zpk) モデルや状態空間 (ss) モデルなど、他の動的システム モデル タイプのインパルス応答を同様にプロットできます。
sys = tf(4,[1 2 10]);
インパルス応答をプロットします。
impulse(sys)
impulse プロットには、定常状態の応答を示す水平の点線が自動的に含まれます。MATLAB® Figure ウィンドウでプロットを右クリックして、ピーク応答や過渡時間など、インパルス応答の他の特性を表示できます。
離散時間システムのインパルス応答をプロットします。システムは 0.2 秒のサンプル時間をもち、次の状態空間行列で表されます。
A = [1.6 -0.7;
1 0];
B = [0.5; 0];
C = [0.1 0.1];
D = 0;状態空間モデルを作成し、そのインパルス応答をプロットします。
sys = ss(A,B,C,D,0.2); impulse(sys)
インパルス応答にはモデルの離散化が反映され、0.2 秒ごとに計算される応答が表示されます。
次の零点-極-ゲイン モデルのインパルス応答を調べます。
sys = zpk(-1,[-0.2+3j,-0.2-3j],1) * tf([1 1],[1 0.05])
sys =
(s+1)^2
----------------------------
(s+0.05) (s^2 + 0.4s + 9.04)
Continuous-time zero/pole/gain model.
Model Properties
impulse(sys)
既定では、impulse は応答が向かっている定常状態を示す終了時間を選択します。過渡応答を詳しく調べるには、インパルス プロットを t = 20 秒に制限します。
impulse(sys,20)
あるいは、インパルス応答を調べる時間が一定間隔で区切られている場合は、正確な時間を指定することができます。たとえば、過渡状態の終わりからシステムが定常状態に到達するまでの応答を調べます。
t = 20:0.2:120; impulse(sys,t)
このプロットは t = 20 で開始されますが、impulse は常にインパルス入力を t = 0 で適用します。
以下の 2 次状態空間モデルについて考えます。
A = [-0.5572,-0.7814;0.7814,0]; B = [1,-1;0,2]; C = [1.9691,6.4493]; sys = ss(A,B,C,0);
このモデルには 2 つの入力と 1 つの出力があるため、最初の入力から出力へと、2 番目の入力から出力への 2 つのチャネルがあります。各チャネルには固有のインパルス応答があります。
impulse を使用すると、すべてのチャネル応答が計算されます。
impulse(sys)
左のプロットには最初の入力チャネルのインパルス応答が表示され、右のプロットには 2 番目の入力チャネルのインパルス応答が表示されます。impulse を使用して MIMO モデルの応答をプロットするたびに、モデルのすべての I/O チャネルを表すプロットの配列が生成されます。たとえば、5 つの状態、3 つの入力、および 2 つの出力をもつランダム状態空間モデルを作成し、そのインパルス応答をプロットします。
sys = rss(5,2,3); impulse(sys)
MATLAB Figure ウィンドウで、プロットを右クリックし、[I/O セレクター] を選択して、プロットをチャネルのサブセットに制限できます。
impulse を使用して、複数の動的システムの応答を同じ軸上にプロットできます。たとえば、PI コントローラーと PID コントローラーでシステムの閉ループ応答を比較します。システムの伝達関数を作成し、コントローラーを調整します。
H = tf(4,[1 2 10]); C1 = pidtune(H,'PI'); C2 = pidtune(H,'PID');
閉ループ システムを形成し、そのインパルス応答をプロットします。
sys1 = feedback(H*C1,1); sys2 = feedback(H*C2,1); impulse(sys1,sys2) legend('PI','PID','Location','SouthEast')
既定では、impulse は、プロットするシステムごとに異なる色を選択します。入力引数 LineSpec を使用して色とライン スタイルを指定できます。
impulse(sys1,'r--',sys2,'b') legend('PI','PID','Location','SouthEast')
最初の LineSpec "'r--' は、PI コントローラーでの応答を表す赤い破線を指定します。2 番目の LineSpec "'b' は、PID コントローラーでの応答を表す青い実線を指定します。凡例に、指定された色とライン スタイルが反映されます。プロットをさらにカスタマイズするには、impulseplot を使用します。
「複数システムのインパルス応答の比較」 の例では、いくつかの個々のシステムの応答を 1 つの軸にプロットする方法を説明しています。モデル配列に複数の動的システムが配置されている場合、impulse はそのすべての応答を一度にプロットします。
モデル配列を作成します。この例では、固有振動数が異なる 2 次伝達関数の 1 次元配列を使用します。最初に、モデル配列のメモリを事前に割り当てます。次のコマンドで、零点とゲインの SISO 伝達関数からなる 1 行 5 列の行を作成します。最初の 2 つの次元は、モデルの出力と入力を表します。残りの次元は配列の次元です
sys = tf(zeros(1,1,1,5));
配列を設定します。
w0 = 1.5:1:5.5; % natural frequencies zeta = 0.5; % damping constant for i = 1:length(w0) sys(:,:,1,i) = tf(w0(i)^2,[1 2*zeta*w0(i) w0(i)^2]); end
(モデル配列とそれらの作成方法の詳細については、モデル配列 (Control System Toolbox)を参照してください)。配列内のすべてのモデルのインパルス応答をプロットします。
impulse(sys)
impulse は、配列内のすべてのエントリの応答に同じライン スタイルを使用します。エントリを区別する 1 つの方法は、動的システム モデルの SamplingGrid プロパティを使用して配列内の各エントリを対応する w0 値に関連付けることです。
sys.SamplingGrid = struct('frequency',w0);次に、応答を MATLAB Figure ウィンドウにプロットする場合は、トレースをクリックして、対応する周波数値を確認できます。
出力引数を指定すると、impulse は応答データの配列を返します。SISO システムの場合、応答データは、応答がサンプリングされる時間点の数と等しい長さの列ベクトルとして返されます。時間点のベクトルを指定するか、impulse でシステム ダイナミクスに基づいて時間点が自動的に選択されるようにします。たとえば、t = 0 ～ t = 5 秒の間、101 の時間点で SISO システムのインパルス応答を抽出します。
sys = tf(4,[1 2 10]); t = 0:0.05:5; y = impulse(sys,t); size(y)
ans = 1×2
101 1
MIMO システムの場合、応答データは次元 N×Ny×Nu の配列で返されます。Ny と Nu は動的システムの出力および入力の数です。たとえば、2 入力、1 出力のシステムを表す、以下の状態空間モデルを考えます。
A = [-0.5572,-0.7814;0.7814,0]; B = [1,-1;0,2]; C = [1.9691,6.4493]; sys = ss(A,B,C,0);
t = 0 ～ t = 20 秒の間、200 の時間点でこのシステムのインパルス応答を抽出します。
t = linspace(0,20,200); y = impulse(sys,t); size(y)
ans = 1×3
200 1 2
y(:,i,j) は、時間 "t" における "j" 番目の入力から "i" 番目の出力へのインパルス応答を含む列ベクトルです。たとえば、2 番目の入力から出力へのインパルス応答を抽出します。
y12 = y(:,1,2); plot(t,y12)
同定されたパラメトリック モデルのインパルス応答を、ノンパラメトリック (実測) モデルのインパルス応答と比較します。また、3 の信頼領域も表示します。
データを読み込みます。
load iddata1 z1
パラメトリック モデルを推定します。
sys1 = ssest(z1,4);
ノンパラメトリック モデルを推定します。
sys2 = impulseest(z1);
比較のためにインパルス応答をプロットします。
t = (0:0.1:10)'; [y1, ~, ~, ysd1] = impulse(sys1,t); [y2, ~, ~, ysd2] = impulse(sys2,t); plot(t, y1, 'b', t, y1+3*ysd1, 'b:', t, y1-3*ysd1, 'b:') hold on plot(t, y2, 'g', t, y2+3*ysd2, 'g:', t, y2-3*ysd2, 'g:')
同定された時系列モデルのインパルス応答を計算します。
時系列モデルは信号モデルとも呼ばれ、測定される入力信号がありません。このモデルのインパルス プロットでは、その (測定されない) ノイズ チャネルを、インパルス信号の適用先の入力チャネルとして使用します。
データを読み込みます。
load iddata9;時系列モデルを推定します。
sys = ar(z9, 4);
sys は形式 A y(t) = e(t) のモデルで、e(t) はノイズ チャネルを表します。インパルス応答を計算するため、e(t) は入力チャネルとして扱われ、e@y1 と名付けられます。
インパルス応答をプロットします。
impulse(sys)
状態空間モデルを作成します。
A = [-0.8429,-0.2134;-0.5162,-1.2139]; B = [0.7254,0.7147;0,-0.2050]; C = [-0.1241,1.4090;1.4897,1.4172]; D = [0.6715,0.7172;-1.2075,0]; sys = ss(A,B,C,D);
既定のオプション セットを作成し、ドット表記を使用して値を指定します。
respOpt = RespConfig; respOpt.Bias = [-2,3]; respOpt.Amplitude = [2,-0.5]; respOpt.InitialState = [0.1,-0.1]; respOpt.Delay = 5;
インパルス応答を計算します。
t = 0:0.1:20; impulse(sys,t,respOpt)
この例では、LPV モデルのインパルス応答をシミュレートする方法を示します。この例では、fcnMaglev.m で定義された浮遊するボールのモデルの外乱 に対する閉ループ応答をシミュレートします。
システムを適切に初期化して = でほぼ維持するように、基準を に設定する必要があります。
モデルを作成し、離散化します。
hmin = 0.05; hmax = 0.25; h0 = (hmin+hmax)/2; Ts = 0.01; Glpv = lpvss("h",@fcnMaglev,0,0,h0); Glpvd = c2d(Glpv,Ts,"tustin");
3 つの高さの値について LPV モデルをサンプリングし、PID コントローラーを調整します。
hpid = linspace(hmin,hmax,3);
[Ga,Goffset] = sample(Glpvd,[],hpid);
wc = 50;
Ka = pidtune(Ga,"pidf",wc);
Ka.Tf = 0.01;ゲイン スケジュール PID コントローラーを作成します。
Ka.SamplingGrid = struct("h",hpid); Koffset = struct("y",{Goffset.u}); Clpv = ssInterpolant(ss(Ka),Koffset);
閉ループ モデルを作成します。
CL = feedback(Glpvd*[1,Clpv],1,2,1);
CL.InputName = {'du';'href'};
CL.OutputName = "h";= の定常状態電流を取得して外乱の大きさを設定します。
[~,~,~,~,~,~,~,u0] = Glpv.DataFunction(0,h0);
と でのインパルス変化に対する応答。
t = 0:Ts:2; pFcn = @(k,x,u) x(1); Config = RespConfig(... Bias=[0;h0], ... Amplitude=0.2*[u0;h0]*Ts, ... Delay=0.5, ... InitialParameter=h0); impulse(CL,t,pFcn,Config) title("Current Impulse Disturbance and Height Impulse Change")
複素係数をもつ状態空間モデルを作成します。
A = [-2-2i -2;1 0]; B = [2;0]; C = [0 0.5+2.5i]; D = 0; sys = ss(A,B,C,D);
システムのインパルス応答を計算します。
[y,t] = impulse(sys);
結果の応答データには複素数の出力値が含まれます。
y
y = 323×1 complex
0.0000 + 0.0000i
0.0674 + 0.2613i
0.1529 + 0.4852i
0.2502 + 0.6728i
0.3537 + 0.8257i
0.4585 + 0.9465i
0.5607 + 1.0378i
0.6570 + 1.1028i
0.7447 + 1.1445i
0.8221 + 1.1663i
0.8877 + 1.1713i
0.9409 + 1.1625i
0.9813 + 1.1428i
1.0090 + 1.1148i
1.0245 + 1.0809i
⋮
入力引数
出力引数
制限
ゼロでない行列 D の連続システムのインパルス応答は t = 0 で無限になります。
impulseはこの不連続を無視し、t = 0 におけるより低い連続値 Cb を返します。impulseコマンドは、内部遅延をもつ連続時間モデルでは機能しません。そのようなモデルでは、pade(Control System Toolbox) を使用してむだ時間を近似してから、インパルス応答を計算します。impulseコマンドは、連続時間 LPV モデルについては、暗黙的なパラメーターの軌跡に沿ったシミュレーションをサポートしていません。
ヒント
任意の入力信号へのシステム応答をシミュレーションするには、
lsimを使用します。追加のプロット カスタマイズ オプションが必要な場合は、代わりに
impulseplotを使用します。impulseを使用して作成されたプロットは、複数行のタイトルや、string 配列または文字ベクトルの cell 配列として指定されたラベルをサポートしません。複数行のタイトルやラベルを指定するには、newline文字を含む単一の string を使用します。impulse(sys) title("first line" + newline + "second line");
アルゴリズム
連続時間 LTI モデルは、まず状態空間形式に変換されます。単入力状態空間モデルのインパルス応答
は初期状態が b の自由応答と等価です。
この応答をシミュレーションするため、システムは入力にゼロ次ホールドを使用して離散化されます。サンプル時間は、時間ベクトル t = T0:dt:Tf が指定されている場合を除き、システム ダイナミクスに基づいて自動的に選択されます。そのため、dt がサンプル時間として使用されます。
バージョン履歴
R2006a より前に導入参考
線形システム アナライザー (Control System Toolbox) | step | lsim | impulseest | pade (Control System Toolbox) | impulseplot
