pade

むだ時間をもつモデルのパデ近似

構文

[num,den] = pade(T,N)

pade(T,N)

sysx = pade(sys,N)

sysx = pade(sys,NU,NY,NINT)

説明

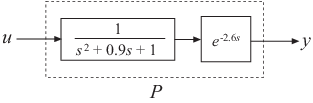
pade は、連続時間 LTL モデルのむだ時間を近似します。このような近似は、連続時間システムのコンテキストにおける伝達遅延や計算遅延などのむだ時間の影響をモデル化する場合に役立ちます。T 秒のむだ時間のラプラス変換は exp(–sT) です。この指数伝達関数は、[1]からのパデ近似式を使用して、有理伝達関数により近似されます。

離散時間モデルを近似するには、absorbDelay を使用します。

むだ時間のあるモデルについての詳細は、線形システムでのむだ時間を参照してください。

[num,den] = pade(T,N) は、むだ時間 T の次数 N のパデ近似を伝達関数形式で返します。出力の行ベクトル num および den は、分子係数と分母係数を s の降べきの順に含みます。num と den は N 次多項式です。

pade(T,N) は、N 次のパデ近似のステップ応答と位相応答をプロットし、むだ時間 T をもつモデルの正確な応答と比較します。結果のパデ近似はすべての周波数で単位ゲインをもちます。

sysx = pade(sys,N) は、連続時間遅延システム sys の、遅延なしの近似 sysx を出力します。すべての遅延はその N 次のパデ近似によって置き換えられます。

sysx = pade(sys,NU,NY,NINT) は、ベクトル NU、NY、NINT をそれぞれ使用して、入力、出力、および I/O または内部遅延のそれぞれについて独立した近似次数を指定します。一貫した近似次数を指定するには、NU、NY、または NINT に対してスカラー値を使用できます。特定の遅延に対する近似を避けるために、NU、NY、または NINT のいくつかの対応する入力に Inf を設定することもできます。

例

2 次パデ近似

この例では、2 次システムでの 1.8 秒のむだ時間について、遅延のない分子係数と分母係数を計算します。

T = 1.8;
N = 2;
[num,den] = pade(T,N)

num = 1×3

    1.0000   -3.3333    3.7037

den = 1×3

    1.0000    3.3333    3.7037

また、遅延のない近似およびむだ時間をもつ元のシステムについて、ステップ応答と位相応答をプロットすることもできます。出力引数を指定せずに pade コマンドを使用して、比較プロットを生成します。

pade(T,N)

連続時間開ループ モデルのパデ近似

この例では、次の連続時間開ループ システムのパデ近似を求めます。

出力遅延をもつ開ループ システムを作成します。

s = tf('s');
T = 2.6;
sys = exp(-T*s)/(s^2+0.9*s+1)

sys =
 
                       1
  exp(-2.6*s) * ---------------
                s^2 + 0.9 s + 1
 
Continuous-time transfer function.

sys は、むだ時間をもつ 2 次伝達関数 (tf) オブジェクトです。

次に、sys の 1 次パデ近似を計算します。

sysx = pade(sys,1)

sysx =
 
             -s + 0.7692
  ----------------------------------
  s^3 + 1.669 s^2 + 1.692 s + 0.7692
 
Continuous-time transfer function.

pade は、sys のすべてのむだ時間を 1 次近似に置き換えます。そのため、sysx は遅延のない 3 次伝達関数になります。

また、遅延のない近似モデルおよびむだ時間をもつモデルのステップ応答と位相応答をプロットして、比較することもできます。むだ時間と次数の値を使用して、プロットを作成します。

pade(T,1)

3 次パデ近似

0.1 秒の I/O 遅延の 3 次パデ近似を計算します。

s = tf('s');
sys = exp(-0.1*s);    
sysx = pade(sys,3)

sysx =
 
  -s^3 + 120 s^2 - 6000 s + 1.2e05
  --------------------------------
  s^3 + 120 s^2 + 6000 s + 1.2e05
 
Continuous-time transfer function.

ここで、sys は 0.1 秒の正確なむだ時間の動的システム表現です。sysx は、その遅延を近似する伝達関数です。

真の遅延とその近似の時間応答と周波数応答を比較します。出力引数なしで pade コマンドを呼び出すと、比較プロットが生成されます。この場合、pade の最初の引数は、むだ時間を表す動的システムでなく、正確なむだ時間の大きさです。

pade(0.1,3)

MIMO 状態空間モデルのパデ近似

この例では、ssModel.mat に含まれる MIMO 状態空間モデル sys について考えます。sys には 2 入力と 3 出力があり、入力遅延、出力遅延、および内部遅延が含まれています。

データを読み込み、sys を調べます。

load('ssModel.mat','sys')
sys

sys =
 
  A = 
            x1       x2
   x1    2.893    1.497
   x2  -0.1138  -0.5279
 
  B = 
             u1        u2
   x1    -1.334    -4.155
   x2     1.127  -0.06161
 
  C = 
            x1       x2
   y1   -2.416  -0.6317
   y2    1.688    1.063
   y3    3.509     1.84
 
  D = 
           u1      u2
   y1   1.019   1.999
   y2       0  -3.658
   y3       0  -5.885
 
  (values computed with all internal delays set to zero)

  Input delays (seconds): 1.5  0.3 
  Output delays (seconds): 0.2  0.8  1.3 
  Internal delays (seconds): 2.1  1.3 
 
Continuous-time state-space model.

入力遅延、出力遅延、および内部遅延の近似次数を指定し、パデ近似を計算します。近似次数を Inf に設定して、対応する遅延の近似を回避します。

NU = [3 Inf];
NY = [1 Inf 2];
NINT = [Inf 2];
sysx = pade(sys,NU,NY,NINT)

sysx =
 
  A = 
             x1       x2       x3       x4       x5       x6       x7       x8       x9      x10
   x1       -10        0        0   -9.665   -2.527   -7.305        0     16.3        0    4.527
   x2         0   -4.615    -3.55    14.04    7.358    21.51        0        0        0        0
   x3         0        2        0        0        0        0        0        0        0        0
   x4         0        0        0    2.893    1.497    4.115        0   -5.335        0   -1.482
   x5         0        0        0  -0.1138  -0.5279  -0.2169        0     4.51        0    1.253
   x6         0        0        0   -8.011   -3.193   -4.615    -3.55        0        0        0
   x7         0        0        0        0        0        2        0        0        0        0
   x8         0        0        0        0        0        0        0       -8   -6.667   -2.222
   x9         0        0        0        0        0        0        0        4        0        0
   x10        0        0        0        0        0        0        0        0        4        0
 
  B = 
              u1        u2
   x1     -4.075     7.996
   x2          0    -23.54
   x3          0         0
   x4      1.334    -4.155
   x5     -1.127  -0.06161
   x6          0      10.1
   x7          0         0
   x8          4         0
   x9          0         0
   x10         0         0
 
  C = 
           x1      x2      x3      x4      x5      x6      x7      x8      x9     x10
   y1       5       0       0   2.416  0.6317   1.826       0  -4.075       0  -1.132
   y2       0       0       0   1.688   1.063   3.074       0       0       0       0
   y3       0  -2.308       0   3.509    1.84   5.377       0       0       0       0
 
  D = 
           u1      u2
   y1   1.019  -1.999
   y2       0  -3.658
   y3       0  -5.885
 
  (values computed with all internal delays set to zero)

  Input delays (seconds): 0  0.3 
  Output delays (seconds): 0  0.8  0 
  Internal delays (seconds): 2.1 
 
Continuous-time state-space model.

対応する近似次数が Inf の場合、結果の近似 sysx にまだ特定の入力遅延、出力遅延、および内部遅延があります。

入力引数

T — むだ時間

正のスカラー

むだ時間の値。正のスカラーとして指定します。ゼロ遅延 (T = 0) のパデ近似は常に単位ゲインです。

N — 連続時間近似モデルの目的の次数

正の整数

連続時間近似モデルの目的の次数。正の整数として指定します。

sys — むだ時間をもつ動的システム

動的システム モデル

むだ時間をもつ動的システム。SISO または MIMO の動的システム モデルとして指定します。使用できる動的システムには次のようなものがあります。

• tf、zpk、ss モデルなどの連続時間 LTI モデル。

• sparss モデルや mechss モデルなどのスパース モデル。

• genss や uss (Robust Control Toolbox) モデルなどの一般化された、あるいは不確かさをもつ LTI モデル。(不確かさをもつモデルを使用するには Robust Control Toolbox™ のライセンスが必要です。)

  結果のモデルでは以下が仮定されます。

  • 調整可能な制御設計ブロックについては調整可能なコンポーネントの現在値

  • 不確かさをもつ制御設計ブロックについてはモデルのノミナル値

• 周波数応答 frd モデル。周波数応答モデルでは、delay2z コマンドを使用して、近似なしで遅延を周波数応答に吸収します。

離散時間モデルの場合は、absorbDelay を使用してください。

NU — 入力チャネルの近似次数

スカラー | ベクトル | Inf

入力チャネルの近似次数。以下として指定します。

• すべての入力で同じ近似次数を使用する場合はスカラー。

• 入力ごとに個別の近似次数値を指定する場合はベクトル。Inf を特定の入力に使用して、対応する遅延の近似を回避することができます。

NY — 出力チャネルの近似次数

スカラー | ベクトル | Inf

出力チャネルの近似次数。以下として指定します。

• すべての出力で同じ近似次数を使用する場合はスカラー。

• 出力ごとに個別の近似次数値を指定する場合はベクトル。Inf を特定の出力に使用して、対応する遅延の近似を回避することができます。

NINT — I/O 遅延または出力遅延の近似次数

スカラー | ベクトル | Inf

I/O 遅延 (伝達関数モデルまたは零点-極-ゲイン モデル) または内部遅延 (状態空間モデル) の近似次数

• すべての I/O 遅延または内部遅延で同じ近似次数を使用する場合はスカラー。

• I/O 遅延または内部遅延ごとに個別の近似次数値を指定する場合はベクトル。Inf を特定の I/O に使用して、対応する遅延の近似を回避することができます。

出力引数

num — 遅延のない伝達関数の分子係数

行ベクトル

遅延のない伝達関数の分子係数。行ベクトルとして返されます。

den — 遅延のない伝達関数の分母係数

行ベクトル

遅延のない伝達関数の分母係数。行ベクトルとして返されます。

sysx — パデ近似されたシステム

モデル オブジェクト

パデ近似されたシステム。sys と同じタイプのモデル オブジェクトとして返されます。

制限

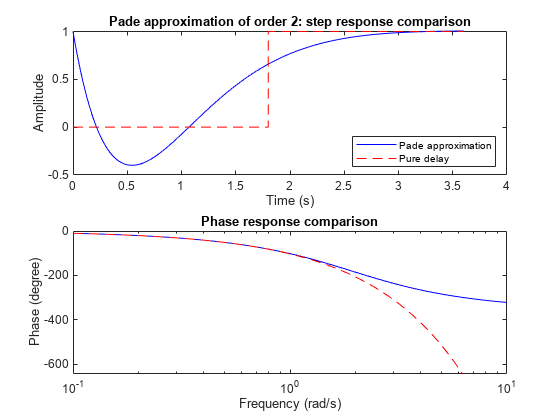
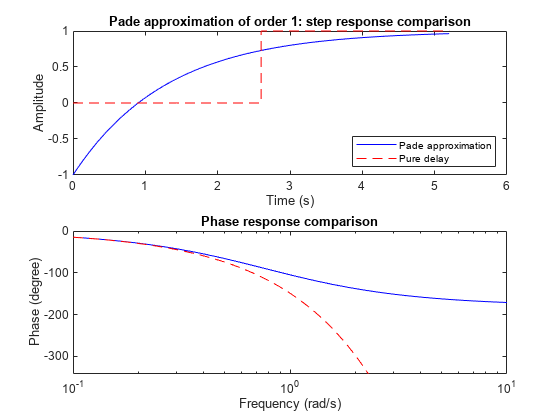
• パデ近似は低周波数でのみ有効であり、時間領域近似よりもすぐれた周波数領域近似を提供します。したがって、真の応答と近似の応答を比較して適切な近似次数を選択し、近似の妥当性を確認してください。

• 高次のパデ近似を計算すると、極が集積した伝達関数ができます。そのような極設定は摂動に極めて敏感になりやすいため、次数 N>10 のパデ近似は避けてください。

参照

[1] Golub, Gene H., and Charles F. Van Loan. Matrix Computations. 2nd ed. Johns Hopkins Series in the Mathematical Sciences 3. Baltimore, Md: Johns Hopkins University Press, 1989. pp. 557-558.

バージョン履歴

R2006a より前に導入

参考

c2d | absorbDelay | thiran | delay2z

トピック

• むだ時間近似
• 線形システムでのむだ時間