dsp.LMSFilter

LMS 適応フィルターの出力、誤差および重みの計算

説明

dsp.LMSFilter System object™ は、次のいずれかのアルゴリズムを使用して、入力信号を目的の信号に収束させる適応有限インパルス応答 (FIR) フィルターを実装します。

• LMS

• 正規化 LMS

• 符号-データ LMS

• 符号-誤差 LMS

• 符号-符号 LMS

これらの各方法の詳細については、アルゴリズムを参照してください。

フィルターは、一次入力信号と目的の信号間での誤差が最小になるまで、その重みを調整します。この誤差の平均二乗 (MSE) は関数 msesim を使用して計算されます。MSE の予測バージョンは関数 msepred でウィーナー フィルターを使用して決定されます。関数 maxstep は、収束速度を制御する最大適応ステップ サイズを計算します。

適応フィルター法の概要と、適応フィルターが使用される最も一般的な用途については、適応フィルターとアプリケーションの概要を参照してください。

適応 FIR フィルターを使用して信号をフィルター処理するには、次のようにします。

1. dsp.LMSFilter オブジェクトを作成し、そのプロパティを設定します。

2. 関数と同様に、引数を指定してオブジェクトを呼び出します。

System object の機能の詳細については、System object とはを参照してください。

この System object は、特定の状況下で SIMD コード生成もサポートします。詳細は、コード生成を参照してください。

作成

構文

lms = dsp.LMSFilter

lms = dsp.LMSFilter(L)

lms = dsp.LMSFilter(Name,Value)

説明

lms = dsp.LMSFilter は、LMS フィルター オブジェクト lms を返します。このオブジェクトは、最小平均二乗 (LMS) アルゴリズムを使用して、与えられた入力と目的の信号に対するフィルター処理された出力、フィルター誤差およびフィルターの重みを計算します。

lms = dsp.LMSFilter(L) は、Length プロパティが L に設定された LMS フィルター オブジェクトを返します。

lms = dsp.LMSFilter(Name,Value) は、指定した各プロパティが指定の値に設定された LMS フィルター オブジェクトを返します。各プロパティ名を一重引用符で囲みます。前の入力引数でもこの構文を使用できます。

プロパティ

特に指定がない限り、プロパティは "調整不可能" です。つまり、オブジェクトの呼び出し後に値を変更することはできません。オブジェクトは呼び出すとロックされ、ロックを解除するには関数 release を使用します。

プロパティが "調整可能" の場合、その値をいつでも変更できます。

プロパティ値の変更の詳細については、System object を使用した MATLAB でのシステム設計を参照してください。

Method — フィルターの重みを計算するメソッド

'LMS' (既定値) | 'Normalized LMS' | 'Sign-Data LMS' | 'Sign-Error LMS' | 'Sign-Sign LMS'

フィルターの重みを計算するメソッド。次のいずれかとして指定します。

• 'LMS' –– Wiener-Hopf 方程式を解き、適応フィルターのフィルター係数を求めます。

• 'Normalized LMS' –– 正規化された LMS アルゴリズムのバリエーション。

• 'Sign-Data LMS' –– 各反復におけるフィルターの重みに対する補正が、入力 x の符号に依存します。

• 'Sign-Error LMS' –– 連続する各反復に対する現在のフィルターの重みに適用される補正が、誤差 err の符号に依存します。

• 'Sign-Sign LMS' –– 連続する各反復に対する現在のフィルターの重みに適用される補正が、x の符号と err の符号の両方に依存します。

アルゴリズムの詳細については、アルゴリズムを参照してください。

Length — FIR フィルターの重みベクトルの長さ

32 (既定値) | 正の整数

FIR フィルターの重みベクトルの長さ。正の整数として指定します。

例: 64

例: 16

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

StepSizeSource — 適応ステップ サイズを指定するメソッド

'Property' (既定値) | 'Input port'

適応ステップ サイズを指定するメソッド。次のいずれかとして指定します。

• 'Property' –– StepSize プロパティは各適応ステップのサイズを指定します。

• 'Input port' –– 適応ステップ サイズをオブジェクトへのいずれかの入力として指定します。

StepSize — 適応ステップ サイズ

0.1 (既定値) | 非負のスカラー

適応ステップ サイズ係数。非負のスカラーとして指定します。正規化された LMS メソッドの収束には、ステップ サイズが 0 より大きく 2 より小さい値でなければなりません。

小さいステップ サイズでは、出力 y と目的の信号d 間の定常偏差が小さくなります。ステップ サイズが小さいと、フィルターの収束速度が減少します。収束速度を向上させるには、ステップ サイズを増やします。大きいステップ サイズではフィルターが不安定になる場合があります。不安定にならずにフィルターが受け入れ可能な最大ステップ サイズを計算するには、関数 maxstep を使用します。

調整可能: Yes

依存関係

このプロパティは StepSizeSource を 'Property' に設定した場合に適用されます。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

LeakageFactor — 漏洩 LMS 法で使用される漏れ係数

1 (既定値) | [0 1]

漏洩 LMS 法の実装時に使用される漏れ係数。範囲 [0 1] 内のスカラーとして指定します。値が 1 と等しい場合、適応されるメソッドに漏れはありません。値が 1 より小さい場合、フィルターは漏洩 LMS 法を実装します。

例: 0.5

調整可能: Yes

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

InitialConditions — フィルターの重みの初期条件

0 (既定値) | スカラー | ベクトル

フィルターの重みの初期条件。スカラーまたは長さが Length プロパティの値に等しいベクトルとして指定します。この入力が実数の場合、このプロパティの値は実数でなければなりません。

例: 0

例: [1 3 1 2 7 8 9 0 2 2 8 2]

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
複素数のサポート: あり

AdaptInputPort — フィルターの重みの調整フラグ

false (既定値) | true

フィルターの重みの調整フラグ。次のいずれかとして指定します。

• false –– オブジェクトは継続的にフィルターの重みを更新します。

• true –– そのアルゴリズムを呼び出すときに、適応制御入力がオブジェクトに与えられます。この入力の値が非ゼロの場合、オブジェクトは継続的にフィルターの重みを更新します。この入力の値がゼロの場合、フィルターの重みは現在の値で保持されます。

WeightsResetInputPort — フィルターの重みのリセット フラグ

false (既定値) | true

フィルターの重みのリセット フラグ。次のいずれかとして指定します。

• false –– オブジェクトは重みをリセットしません。

• true –– そのアルゴリズムを呼び出すときに、リセット制御入力がオブジェクトに与えられます。この設定によって WeightsResetCondition プロパティが有効になります。オブジェクトは、WeightsResetCondition プロパティとオブジェクト アルゴリズムに与えられたリセット入力の値に基づいてフィルターの重みをリセットします。

WeightsResetCondition — フィルターの重みのリセット イベント

'Non-zero' (既定値) | 'Rising edge' | 'Falling edge' | 'Either edge'

フィルターの重みのリセットをトリガーするイベント。次のいずれかとして指定します。リセット入力でリセット イベントが検出されるたびに、オブジェクトはフィルターの重みをリセットします。

• 'Non-zero' — リセット入力がゼロではない場合に各サンプルでリセット操作をトリガーします。

• 'Rising edge' — リセット入力が次のいずれかを行うときにリセット操作をトリガーします。

  • 負の値から正の値またはゼロに立ち上がる。

  • ゼロから正の値へ立ち上がる。この場合、立ち上がりは負の値からゼロへの立ち上がりと連続していません。

    

• 'Falling edge' — リセット入力が次のいずれかを行うときにリセット操作をトリガーします。

  • 正の値から負の値またはゼロに立ち下がる。

  • ゼロから負の値に立ち下がる。この場合、立ち下がりは正の値からゼロへの立ち下りと連続していません。

    

• 'Either edge' — リセット入力が立ち上がりエッジまたは立ち下がりエッジの場合にリセット操作をトリガーします。

オブジェクトは、このプロパティとオブジェクト アルゴリズムに与えられたリセット入力 r の値に基づいてフィルターの重みをリセットします。

依存関係

このプロパティは、WeightsResetInputPortプロパティを true に設定した場合に適用されます。

WeightsOutput — 適応させたフィルターの重みを出力するメソッド

'Last' (既定値) | 'None' | 'All'

適応させたフィルターの重みを出力するメソッド。次のいずれかとして指定します。

• 'Last' (既定) — オブジェクトはデータ フレームの最後のサンプルに対応する重みの列ベクトルを返します。重みベクトルの長さは Length プロパティで指定された値になります。

• 'All' — オブジェクトは FrameLength 行 Length 列の重みの行列を返します。行列は、入力値の FrameLength サンプルすべての重みの履歴について、サンプルごとに完全に対応します。行列の各行は、対応する入力サンプルについて計算された一連の LMS フィルターの重みに対応します。

• 'None' — この設定にすると、重みの出力が無効になります。

固定小数点プロパティ

RoundingMethod — 固定小数点演算の丸め手法

'Floor' (既定値) | 'Ceiling' | 'Convergent' | 'Nearest' | 'Round' | 'Simplest' | 'Zero'

固定小数点演算の丸めモードを指定します。詳細については、丸めモードを参照してください。

OverflowAction — 固定小数点演算のオーバーフロー アクション

'Wrap' (既定値) | 'Saturate'

固定小数点演算のオーバーフロー アクション。次のいずれかを指定します。

• 'Wrap' –– オブジェクトはその固定小数点演算の結果をラップします。

• 'Saturate' –– オブジェクトはその固定小数点演算の結果を飽和します。

オーバーフロー アクションの詳細については、固定小数点演算のオーバーフロー モードを参照してください。

StepSizeDataType — ステップ サイズの語長と小数部の長さの設定

'Same word length as first input' (既定値) | 'Custom'

ステップ サイズの語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same word length as first input' –– オブジェクトはステップ サイズの語長を最初の入力と同じになるように指定します。小数部の長さは、可能な最高の精度になるように計算されます。

• 'Custom' –– ステップ サイズのデータ型は、CustomStepSizeDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用するステップ サイズのデータ型の詳細については、固定小数点 のセクションを参照してください。

CustomStepSizeDataType — ステップ サイズの語長と小数部の長さ

numerictype([],16,15) (既定値)

ステップ サイズの語長と小数部の長さ。語長が 16 で小数部の長さが 15 の自動符号付きの数値型として指定します。

例: numerictype([],32)

依存関係

このプロパティは、次の条件において適用されます。

• StepSizeSource プロパティが 'Property' に、StepSizeDataType が 'Custom' に設定されている。

• StepSizeSource プロパティが 'Input port' に設定されている。

LeakageFactorDataType — 漏れ係数の語長と小数部の長さの設定

'Same word length as first input' (既定値) | 'Custom'

漏れ係数の語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same word length as first input' –– オブジェクトは漏れ係数の語長を最初の入力と同じになるように指定します。小数部の長さは、可能な最高の精度になるように計算されます。

• 'Custom' –– 漏れ係数のデータ型は、CustomLeakageFactorDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用する漏れ係数のデータ型の詳細については、固定小数点 のセクションを参照してください。

CustomLeakageFactorDataType — 漏れ係数の語長と小数部の長さ

numerictype([],16,15) (既定値)

漏れ係数の語長と小数部の長さ。語長が 16 で小数部の長さが 15 の自動符号付きの数値型として指定します。

例: numerictype([],32)

依存関係

このプロパティは、LeakageFactorDataType プロパティを 'Custom' に設定した場合に適用されます。

WeightsDataType — 重みの語長と小数部の長さの設定

'Same as first input' (既定値) | 'Custom'

重みの語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same as first input' –– オブジェクトはフィルターの重みのデータ型を最初の入力と同じになるように指定します。

• 'Custom' –– フィルターの重みのデータ型は、CustomWeightsDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用するフィルターの重みのデータ型の詳細については、固定小数点 のセクションを参照してください。

CustomWeightsDataType — フィルターの重みの語長と小数部の長さ

numerictype([],16,15) (既定値)

フィルターの重みの語長と小数部の長さ。語長が 16 で小数部の長さが 15 の自動符号付きの数値型として指定します。

例: numerictype([],32,20)

依存関係

このプロパティは、WeightsDataType プロパティを 'Custom' に設定した場合に適用されます。

EnergyProductDataType — エネルギー積の語長と小数部の長さの設定

'Same as first input' (既定値) | 'Custom'

エネルギー積の語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same as first input' –– オブジェクトはエネルギー積のデータ型を最初の入力と同じになるように指定します。

• 'Custom' –– エネルギー積のデータ型は、CustomEnergyProductDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用するエネルギー積のデータ型の詳細については、固定小数点 のセクションを参照してください。

依存関係

このプロパティは、Method プロパティを 'Normalized LMS' に設定した場合に適用されます。

CustomEnergyProductDataType — エネルギー積の語長と小数部の長さ

numerictype([],32,20) (既定値)

エネルギー積の語長と小数部の長さ。語長が 32 で小数部の長さが 20 の自動符号付きの数値型として指定します。

依存関係

このプロパティは、Method プロパティを 'Normalized LMS' に、EnergyProductDataType プロパティを 'Custom' に設定した場合に適用されます。

EnergyAccumulatorDataType — エネルギー アキュムレータの語長と小数部の長さの設定

'Same as first input' (既定値) | 'Custom'

エネルギー アキュムレータの語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same as first input' –– オブジェクトはエネルギー アキュムレータのデータ型を最初の入力と同じになるように指定します。

• 'Custom' –– エネルギー アキュムレータのデータ型は、CustomEnergyAccumulatorDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用するエネルギー アキュムレータのデータ型の詳細については、固定小数点 のセクションを参照してください。

依存関係

このプロパティは、Method プロパティを 'Normalized LMS' に設定した場合に適用されます。

CustomEnergyAccumulatorDataType — エネルギー アキュムレータの語長と小数部の長さ

numerictype([],32,20) (既定値)

エネルギー アキュムレータの語長と小数部の長さ。語長が 32 で小数部の長さが 20 の自動符号付きの数値型として指定します。

依存関係

このプロパティは、Method プロパティを 'Normalized LMS' に、EnergyAccumulatorDataType プロパティを 'Custom' に設定した場合に適用されます。

ConvolutionProductDataType — 畳み込み積の語長と小数部の長さの設定

'Same as first input' (既定値) | 'Custom'

畳み込み積の語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same as first input' –– オブジェクトは畳み込み積のデータ型を最初の入力と同じになるように指定します。

• 'Custom' –– 畳み込み積のデータ型は、CustomConvolutionProductDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用する畳み込み積のデータ型の詳細については、固定小数点 のセクションを参照してください。

CustomConvolutionProductDataType — 畳み込み積の語長と小数部の長さ

numerictype([],32,20) (既定値)

畳み込み積の語長と小数部の長さ。語長が 32 で小数部の長さが 20 の自動符号付きの数値型として指定します。

依存関係

このプロパティは、ConvolutionProductDataType プロパティを 'Custom' に設定した場合に適用されます。

ConvolutionAccumulatorDataType — 畳み込みアキュムレータの語長と小数部の長さの設定

'Same as first input' (既定値) | 'Custom'

畳み込みアキュムレータの語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same as first input' –– オブジェクトは畳み込みアキュムレータのデータ型を最初の入力と同じになるように指定します。

• 'Custom' –– 畳み込みアキュムレータのデータ型は、CustomConvolutionAccumulatorDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用する畳み込みアキュムレータのデータ型の詳細については、固定小数点 のセクションを参照してください。

CustomConvolutionAccumulatorDataType — 畳み込みアキュムレータの語長と小数部の長さ

numerictype([],32,20) (既定値)

畳み込みアキュムレータの語長と小数部の長さ。語長が 32 で小数部の長さが 20 の自動符号付きの数値型として指定します。

依存関係

このプロパティは、ConvolutionAccumulatorDataType プロパティを 'Custom' に設定した場合に適用されます。

StepSizeErrorProductDataType — ステップ サイズの誤差の積の語長と小数部の長さの設定

'Same as first input' (既定値) | 'Custom'

ステップ サイズの誤差の積の語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same as first input' –– オブジェクトはステップ サイズの誤差の積のデータ型を最初の入力と同じになるように指定します。

• 'Custom' –– ステップ サイズの誤差の積のデータ型は、CustomStepSizeErrorProductDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用するステップ サイズの誤差の積のデータ型の詳細については、固定小数点 のセクションを参照してください。

CustomStepSizeErrorProductDataType — ステップ サイズの誤差の積の語長と小数部の長さ

numerictype([],32,20) (既定値)

ステップ サイズの誤差の積の語長と小数部の長さ。語長が 32 で小数部の長さが 20 の自動符号付きの数値型として指定します。

依存関係

このプロパティは、StepSizeErrorProductDataType プロパティを 'Custom' に設定した場合に適用されます。

WeightsUpdateProductDataType — フィルターの重み更新の積の語長と小数部の長さの設定

'Same as first input' (既定値) | 'Custom'

フィルターの重み更新の積の語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same as first input' –– オブジェクトはフィルターの重み更新の積のデータ型を最初の入力と同じになるように指定します。

• 'Custom' –– フィルターの重み更新の積のデータ型は、CustomWeightsUpdateProductDataType プロパティを使ってカスタムの数値型として指定されます。

このオブジェクトが使用するフィルターの重み更新の積のデータ型の詳細については、固定小数点 のセクションを参照してください。

CustomWeightsUpdateProductDataType — フィルターの重み更新の積の語長と小数部の長さ

numerictype([],32,20) (既定値)

フィルターの重み更新の積の語長と小数部の長さ。語長が 32 で小数部の長さが 20 の自動符号付きの数値型として指定します。

依存関係

このプロパティは、WeightsUpdateProductDataType プロパティを 'Custom' に設定した場合に適用されます。

QuotientDataType — 商の語長と小数部の長さの設定

'Same as first input' (既定値) | 'Custom'

商の語長と小数部の長さの設定。次のいずれかとして指定します。

• 'Same as first input' –– オブジェクトは商のデータ型を最初の入力のデータ型と同じになるように指定します。

• 'Custom' –– 商のデータ型は、CustomQuotientDataType プロパティを使ってカスタムの数値型として指定します。

このオブジェクトが使用する商のデータ型の詳細については、固定小数点 のセクションを参照してください。

依存関係

このプロパティは、Method プロパティを 'Normalized LMS' に設定した場合に適用されます。

CustomQuotientDataType — 商の語長と小数部の長さ

numerictype([],32,20) (既定値)

フィルターの重み更新の積の語長と小数部の長さ。語長が 32 で小数部の長さが 20 の自動符号付きの数値型として指定します。

依存関係

このプロパティは、Method プロパティを 'Normalized LMS' に、QuotientDataType プロパティを 'Custom' に設定した場合に適用されます。

使用法

構文

[y,err,wts] = lms(x,d)

[y,err] = lms(x,d)

[___] = lms(x,d,mu)

[___] = lms(x,d,a)

[___] = lms(x,d,r)

[y,err,wts] = lms(x,d,mu,a,r)

説明

[y,err,wts] = lms(x,d) は、目的の信号として d を使用して入力信号 x をフィルター処理し、フィルター処理された出力を y に、フィルター誤差を err に、推定されたフィルターの重みを wts に返します。LMS フィルター オブジェクトは、出力信号と目的の信号の間で誤差を最小化するために必要なフィルターの重みを推定します。

[y,err] = lms(x,d) は、WeightsOutput プロパティが 'None' に設定されると、目的の信号として d を使用して入力信号 x をフィルター処理し、フィルター処理された出力を y に、フィルター誤差を err に返します。

[___] = lms(x,d,mu) は、StepSizeSource プロパティが 'Input port' に設定されると、目的の信号として d、ステップ サイズとして mu を使用して入力信号 x をフィルター処理します。これらの入力は、前のいずれの出力セットでも使用できます。

[___] = lms(x,d,a) は、AdaptInputPort プロパティが true に設定されると、目的の信号として d、適応制御として a を使用して入力信号 x をフィルター処理します。a が非ゼロの場合、System object は継続的にフィルターの重みを更新します。a がゼロの場合、フィルターの重みは一定になります。

[___] = lms(x,d,r) は、WeightsResetInputPort プロパティが true に設定されると、目的の信号として d、リセット信号として r を使用して入力信号 x をフィルター処理します。WeightsResetCondition プロパティはリセットのトリガー条件の設定に使用できます。リセット イベントが発生すると、System object は、フィルターの重みをその初期値にリセットします。

[y,err,wts] = lms(x,d,mu,a,r) は、目的の信号として d、ステップ サイズとして mu、適応制御として a、リセット信号として r を使用して入力信号 x をフィルター処理し、フィルター処理された出力を y に、フィルター誤差を err に、適応させたフィルターの重みを wts に返します。

入力引数

x — データ入力

スカラー | 列ベクトル

LMS フィルターでフィルター処理される信号。入力 x と目的の信号 d はサイズ、データ型、実数/複素数が同じでなければなりません。入力が固定小数点の場合、データ型は符号付きでなければならず、目的の信号と同じ語長をもたなければなりません。

入力 x は可変サイズ信号にすることができます。オブジェクトがロックされていても、列ベクトルの要素数を変更できます。System object はオブジェクトを呼び出してそのアルゴリズムを実行するときにロックします。

データ型: single | double | int8 | int16 | int32 | int64 | fi
複素数のサポート: あり

d — 目的の信号

スカラー | 列ベクトル

LMS フィルターはそのフィルターの重み wts を調整して誤差 err を最小化し、入力信号 x を目的の信号 d に可能な限り近づけて収束させます。

入力 x と目的の信号 d はサイズ、データ型、実数/複素数が同じでなければなりません。目的の信号が固定小数点の場合、データ型は符号付きでなければならず、データ入力と同じ語長をもたなければなりません。

入力 d は可変サイズ信号にすることができます。オブジェクトがロックされていても、列ベクトルの要素数を変更できます。System object はオブジェクトを呼び出してそのアルゴリズムを実行するときにロックします。

データ型: single | double | int8 | int16 | int32 | int64 | fi
複素数のサポート: あり

mu — ステップ サイズ

非負のスカラー

適応ステップ サイズ係数。非負の数値スカラーとして指定します。正規化された LMS メソッドの収束には、ステップ サイズが 0 より大きく 2 より小さい値でなければなりません。ステップ サイズ入力のデータ型は x と d のデータ型と一致しなければなりません。データ型が固定小数点の場合、データ型は符号付きでなければなりません。

小さいステップ サイズでは、出力 y と目的の信号 d 間の定常偏差が小さくなります。ステップ サイズが小さいと、フィルターの収束速度が減少します。収束速度を向上させるには、ステップ サイズを増やします。大きいステップ サイズではフィルターが不安定になる場合があります。不安定にならずにフィルターが受け入れ可能な最大ステップ サイズを計算するには、関数 maxstep を使用します。

依存関係

この入力は StepSizeSource プロパティが 'Input port' に設定されている場合に必要です。

データ型: single | double | int8 | int16 | int32 | int64 | fi

a — 適応制御

スカラー

フィルターの重みの更新方法を制御する適応制御入力。この入力の値が非ゼロの場合、オブジェクトは継続的にフィルターの重みを更新します。この入力の値がゼロの場合、フィルターの重みは現在の値で保持されます。

依存関係

この入力は AdaptInputPort プロパティが true に設定されている場合に必要です。

データ型: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical

r — リセット信号

スカラー

WeightsResetCondition プロパティの値に基づいてフィルターの重みをリセットするリセット信号。

依存関係

この入力は WeightsResetInputPort プロパティが true に設定されている場合に必要です。

データ型: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical

出力引数

y — フィルター処理された出力

スカラー | 列ベクトル

フィルター処理された出力。スカラーまたは列ベクトルとして返されます。オブジェクトはそのフィルターの重みを調整して入力信号 x が目的の信号 d に一致するように収束させます。フィルターは収束した信号を出力します。

データ型: single | double | int8 | int16 | int32 | int64 | fi
複素数のサポート: あり

err — 出力と目的の信号の差異

スカラー | 列ベクトル

出力信号 y と目的の信号 d の差異。スカラーまたは列ベクトルとして返されます。err のデータ型は y のデータ型と一致します。適応フィルターの目的は、この誤差を最小化することです。オブジェクトはその重みを調整して収束させ、目的の信号とよく一致する出力信号を生成する最適なフィルターの重みになるようにします。err が計算される方法の詳細については、アルゴリズムを参照してください。

データ型: single | double | int8 | int16 | int32 | int64 | fi

wts — 適応フィルターの重み

スカラー | 列ベクトル

適応フィルターの重み。スカラーまたは Length の値で指定された長さの列ベクトルとして返されます。

データ型: single | double | int8 | int16 | int32 | int64 | fi

オブジェクト関数

オブジェクト関数を使用するには、System object を最初の入力引数として指定します。たとえば、obj という名前の System object のシステム リソースを解放するには、次の構文を使用します。

release(obj)

dsp.LMSFilter に固有

maxstep	Maximum step size for LMS adaptive filter convergence
msepred	Predicted mean squared error for LMS adaptive filter
msesim	Estimated mean squared error for adaptive filters

すべての System object に共通

step	System object のアルゴリズムの実行
release	リソースを解放し、System object のプロパティ値と入力特性の変更を可能にします。
reset	System object の内部状態のリセット

例

LMS フィルターに対する平均二乗誤差の予測

平均二乗誤差 (MSE) は、目的の信号と適応フィルターへの一次入力信号との間の誤差の二乗平均を測定します。この誤差が減少すると、一次入力が目的の信号に収束します。関数 msepred と関数 msesim を使用した各時点での MSE の予測値と MSE のシミュレーション値を決定します。最小 MSE と定常状態 MSE 値に関してこれらの MSE 値を互いに比較します。また、係数の共分散行列のトレースで与えられる係数誤差の二乗の和を計算します。

メモ: R2016a 以前のリリースを使用している場合、それぞれのオブジェクトの呼び出しを等価な step 構文で置き換えてください。たとえば、obj(x) は step(obj,x) になります。

初期化

未知のシステムを表す dsp.FIRFilter System object™ を作成します。信号 x を FIR フィルターに渡します。未知のシステムの出力は、未知のシステム (FIR フィルター) の出力の和である目的の信号 d と、加法性ノイズ信号 n です。

num = fir1(31,0.5);
fir = dsp.FIRFilter('Numerator',num);  
iir = dsp.IIRFilter('Numerator',sqrt(0.75),...
        'Denominator',[1 -0.5]);
x = iir(sign(randn(2000,25))); 
n = 0.1*randn(size(x));           
d = fir(x) + n; 

LMS フィルター

目的の信号の出力に適応するフィルターを作成する dsp.LMSFilter System object を作成します。適応フィルターの長さを 32 タップ、ステップ サイズを 0.008、解析とシミュレーションの間引き係数を 5 に設定します。変数 simmse は、未知のシステム d の出力と適応フィルターの出力との間でシミュレーションされた MSE を表します。変数 mse は対応する予測された値を与えます。

l = 32;
mu = 0.008;
m  = 5;

lms = dsp.LMSFilter('Length',l,'StepSize',mu);
[mmse,emse,meanW,mse,traceK] = msepred(lms,x,d,m);
[simmse,meanWsim,Wsim,traceKsim] = msesim(lms,x,d,m);

MSE 結果のプロット

シミュレーション MSE 値、予測 MSE 値、最小 MSE 値、最終 MSE 値を比較します。最終 MSE 値は最小 MSE と超過 MSE の和で与えられます。

nn = m:m:size(x,1);
semilogy(nn,simmse,[0 size(x,1)],[(emse+mmse)...
    (emse+mmse)],nn,mse,[0 size(x,1)],[mmse mmse])
title('Mean Squared Error Performance')
axis([0 size(x,1) 0.001 10])
legend('MSE (Sim.)','Final MSE','MSE','Min. MSE')
xlabel('Time Index')
ylabel('Squared Error Value')

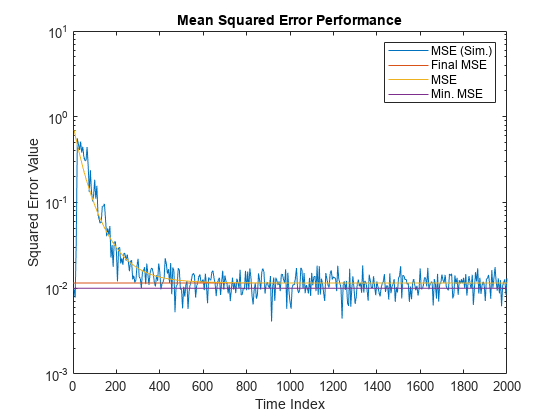
予測 MSE はシミュレーション MSE と同じ軌跡に従います。両方の軌跡は定常状態 (最終) MSE で収束します。

係数軌跡のプロット

meanWsim は msesim によって与えられたシミュレーション係数の平均値です。meanW は msepred によって与えられた予測係数の平均値です。

LMS フィルター係数 12、13、14、15 のシミュレーション平均値と予測平均値を比較します。

plot(nn,meanWsim(:,12),'b',nn,meanW(:,12),'r',nn,...
meanWsim(:,13:15),'b',nn,meanW(:,13:15),'r')
PlotTitle ={'Average Coefficient Trajectories for';...
            'W(12), W(13), W(14), and W(15)'}

PlotTitle = 2x1 cell
    {'Average Coefficient Trajectories for'}
    {'W(12), W(13), W(14), and W(15)'      }

title(PlotTitle)
legend('Simulation','Theory')
xlabel('Time Index')
ylabel('Coefficient Value')

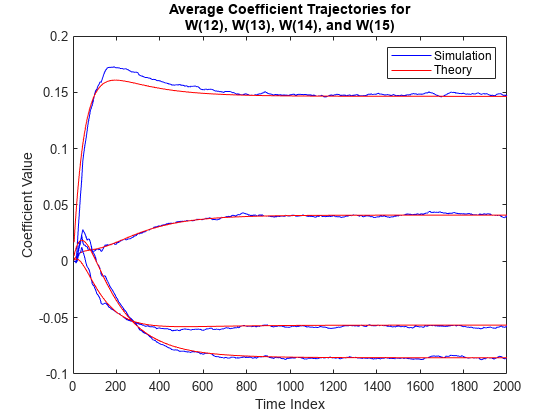
定常状態では、両方の軌跡が収束します。

二乗係数誤差の合計

msepred と msesim で与えられた二乗係数誤差の合計を比較します。これらの値は係数の共分散行列のトレースで与えられます。

semilogy(nn,traceKsim,nn,traceK,'r')
title('Sum-of-Squared Coefficient Errors')
axis([0 size(x,1) 0.0001 1])
legend('Simulation','Theory')
xlabel('Time Index')
ylabel('Squared Error Value')

LMS 適応フィルターの最大ステップの計算

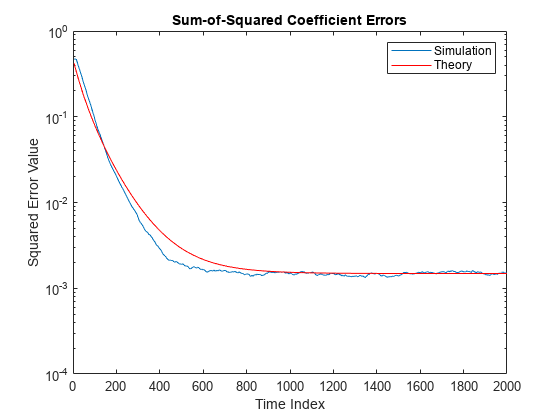
関数 maxstep は、適応フィルターの最大ステップ サイズを計算します。このステップ サイズはフィルターをその取り得る最大収束速度で安定させます。ランダムな符号付き信号を IIR フィルターに渡して、一次入力信号 x を作成します。信号 x にはフレームあたり 2000 サンプルの 50 フレームが含まれます。32 タップと 0.1 のステップ サイズで LMS フィルターを作成します。

x = zeros(2000,50);
IIRFilter = dsp.IIRFilter('Numerator',sqrt(0.75),...
    'Denominator',[1 -0.5]);
for k = 1:size(x,2)   
  x(:,k) = IIRFilter(sign(randn(size(x,1),1))); 
end
mu = 0.1;     
LMSFilter = dsp.LMSFilter('Length',32,...
    'StepSize',mu);

関数 maxstep を使用して、最大適応ステップ サイズと平均二乗の点における最大ステップ サイズを計算します。

[mumax,mumaxmse] = maxstep(LMSFilter,x)

mumax = 0.0625

mumaxmse = 0.0536

LMS アルゴリズムの使用による FIR フィルターのシステム同定

システム同定は、適応フィルターを使用して未知のシステムの係数を特定するプロセスです。このプロセスの概要は、システム同定 –– 適応フィルターの使用による未知のシステムの同定に示されています。関係する主なコンポーネントは以下のとおりです。

• 適応フィルター アルゴリズム。この例では、dsp.LMSFilter の Method プロパティを 'LMS' に設定して、LMS 適応フィルター アルゴリズムを選択します。

• 適応対象となる未知のシステムまたはプロセス。この例では、fircband で設計されたフィルターが未知のシステムです。

• 適応プロセスを実行する適切な入力データ。一般的な LMS モデルの場合、これらは目的の信号 $\mathit{d}\left(\mathit{k}\right)$ と入力信号 $\mathit{x}\left(\mathit{k}\right)$ です。

適応フィルターの目的は、適応フィルターの出力 $\mathit{y}\left(\mathit{k}\right)$ と未知のシステム (同定対象のシステム) の出力 $\mathit{d}\left(\mathit{k}\right)$ の間で誤差信号を最小化することです。誤差信号が最小化されると、適応させたフィルターは未知のシステムに似たものになります。両方のフィルターの係数は、ほぼ一致します。

メモ: R2016a 以前のリリースを使用している場合、それぞれのオブジェクトの呼び出しを等価な step 構文で置き換えてください。たとえば、obj(x) は step(obj,x) になります。

未知のシステム

同定対象のシステムを表す dsp.FIRFilter オブジェクトを作成します。関数 fircband を使用して、フィルターの係数を設計します。設計するフィルターは、阻止帯域で 0.2 リップルに制約されているローパス フィルターです。

filt = dsp.FIRFilter;
filt.Numerator = fircband(12,[0 0.4 0.5 1],[1 1 0 0],[1 0.2],... 
{'w' 'c'});

信号 x を FIR フィルターに渡します。目的の信号 d は、未知のシステム (FIR フィルター) の出力と加法性ノイズ信号 n の和です。

x = 0.1*randn(250,1);
n = 0.01*randn(250,1);
d = filt(x) + n;

適応フィルター

未知のフィルターを設計して目的の信号の準備ができたので、適応 LMS フィルター オブジェクトを作成および適用して未知のフィルターを特定します。

適応フィルター オブジェクトを準備するには、フィルターの係数を推定するための開始値と LMS のステップ サイズ (mu) が必要です。フィルター係数の推定値として、一連の非ゼロ値で始めることができます。この例では、13 個のフィルターの重みの初期値にゼロを使用します。dsp.LMSFilter の InitialConditions プロパティをフィルターの重みの目的の初期値に設定します。ステップ サイズについては、250 回の反復 (250 個の入力サンプル点) で適切に収束するための十分に大きい値と未知のフィルターを正確に推定するための十分に小さい値の間にある、0.8 が良い妥協点です。

LMS 適応アルゴリズムを使用する適応フィルターを表す dsp.LMSFilter オブジェクトを作成します。適応フィルターの長さを 13 タップ、ステップ サイズを 0.8 に設定します。

mu = 0.8;
lms = dsp.LMSFilter(13,'StepSize',mu)

lms = 
  dsp.LMSFilter with properties:

                   Method: 'LMS'
                   Length: 13
           StepSizeSource: 'Property'
                 StepSize: 0.8000
            LeakageFactor: 1
        InitialConditions: 0
           AdaptInputPort: false
    WeightsResetInputPort: false
            WeightsOutput: 'Last'

  Show all properties

一次入力信号 x と目的の信号 d を LMS フィルターに渡します。適応フィルターを稼働させて、未知のシステムを特定します。適応フィルターの出力 y は目的の信号 d に収束された信号であり、2 つの信号間の誤差 e を最小化します。

結果をプロットします。出力信号と目的の信号が期待どおりには一致しておらず、これらの間の誤差は無視できません。

[y,e,w] = lms(x,d);
plot(1:250, [d,y,e])
title('System Identification of an FIR filter')
legend('Desired','Output','Error')
xlabel('Time index')
ylabel('Signal value')

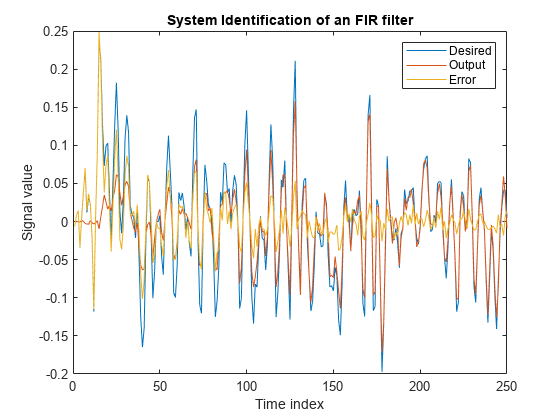
重みの比較

重みベクトル w は、未知のシステム (FIR フィルター) に似るように適応させた LMS フィルターの係数を表します。収束を確認するために、FIR フィルターの分子係数と適応フィルターの推定された重み付けを比較します。

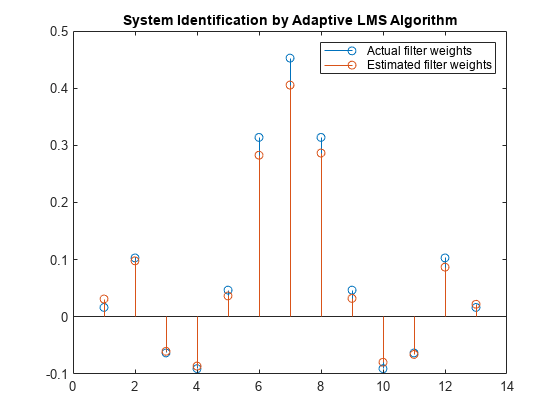
前の信号プロットの結果を確認すると、推定されたフィルターの重みと実際のフィルターの重みが十分には一致していません。

stem([(filt.Numerator).' w])
title('System Identification by Adaptive LMS Algorithm')
legend('Actual filter weights','Estimated filter weights',...
       'Location','NorthEast')

ステップ サイズの変更

実験的に、ステップ サイズを 0.2 に変更してみます。mu = 0.2 を使用して例を繰り返すと、以下のステム プロットが出力されます。フィルターは収束せず、推定された重みは実際の重みの良好な近似にはなっていません。

mu = 0.2;
lms = dsp.LMSFilter(13,'StepSize',mu);
[~,~,w] = lms(x,d);
stem([(filt.Numerator).' w])
title('System Identification by Adaptive LMS Algorithm')
legend('Actual filter weights','Estimated filter weights',...
       'Location','NorthEast')

データ サンプル数の増加

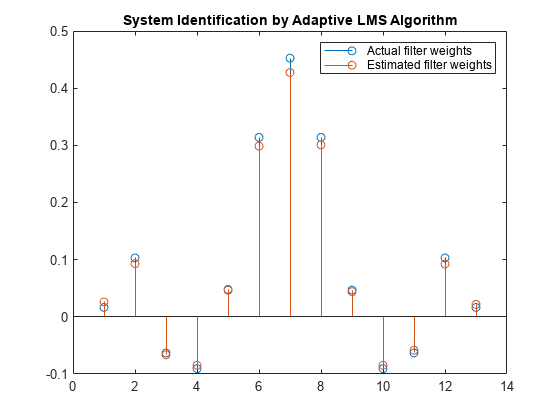
目的の信号のフレーム サイズを大きくします。これにより必要な計算量が増えますが、適応に使用できるデータがより多く LMS アルゴリズムに与えられます。信号データのサンプルを 1000 個、ステップ サイズを 0.2 にすると、係数が前より一致するようになり、収束が改善されることがわかります。

release(filt);
x = 0.1*randn(1000,1);
n = 0.01*randn(1000,1);
d = filt(x) + n;
[y,e,w] = lms(x,d);
stem([(filt.Numerator).' w])
title('System Identification by Adaptive LMS Algorithm')
legend('Actual filter weights','Estimated filter weights',...
       'Location','NorthEast')

反復処理でデータを入力して、データ サンプル数をさらに増やします。1000 サンプルずつまとめて 4 回の反復で渡して、4000 サンプルのデータに対して LMS アルゴリズムを実行します。

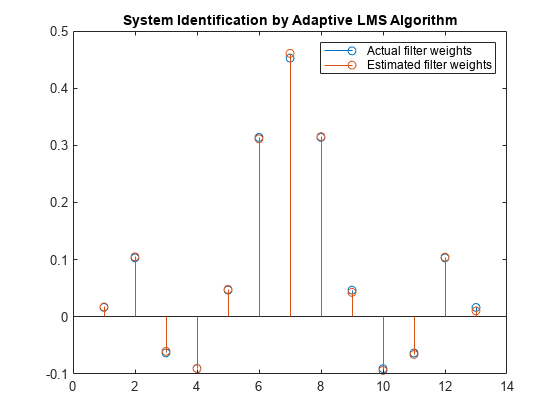
フィルターの重みを比較します。LMS フィルターの重みが FIR フィルターの重みと非常によく一致しているので、収束が適切であることがわかります。

release(filt);
n = 0.01*randn(1000,1);
for index = 1:4
  x = 0.1*randn(1000,1);
  d = filt(x) + n;
  [y,e,w] = lms(x,d);
end
stem([(filt.Numerator).' w])
title('System Identification by Adaptive LMS Algorithm')
legend('Actual filter weights','Estimated filter weights',...
       'Location','NorthEast')

出力信号と目的の信号が非常によく一致しており、これらの間の誤差はゼロに近くなっています。

plot(1:1000, [d,y,e])
title('System Identification of an FIR filter')
legend('Desired','Output','Error')
xlabel('Time index')
ylabel('Signal value')

正規化 LMS アルゴリズムの使用による FIR フィルターのシステム同定

LMS アルゴリズムの収束性能を向上するために、正規化されたバリアント (NLMS) は信号強度に基づいて適応ステップ サイズを使用します。入力信号強度が変化すると、アルゴリズムによって入力強度が計算され、適切な値を維持するようにステップ サイズが調整されます。ステップ サイズは時間と共に変化するため、正規化アルゴリズムは多くの場合、少ないサンプル数でより迅速に収束します。時間と共に緩やかに変化する入力信号の場合、正規化 LMS アルゴリズムがより効率的な LMS の手法となります。

LMS のアプローチを使用する例については、LMS アルゴリズムの使用による FIR フィルターのシステム同定を参照してください。

メモ: R2016a 以前のリリースを使用している場合、それぞれのオブジェクトの呼び出しを等価な step 構文で置き換えてください。たとえば、obj(x) は step(obj,x) になります。

未知のシステム

同定対象のシステムを表す dsp.FIRFilter オブジェクトを作成します。関数 fircband を使用して、フィルターの係数を設計します。設計するフィルターは、阻止帯域で 0.2 リップルに制約されているローパス フィルターです。

filt = dsp.FIRFilter;
filt.Numerator = fircband(12,[0 0.4 0.5 1],[1 1 0 0],[1 0.2],... 
{'w' 'c'});

信号 x を FIR フィルターに渡します。目的の信号 d は、未知のシステム (FIR フィルター) の出力と加法性ノイズ信号 n の和です。

x = 0.1*randn(1000,1);
n = 0.001*randn(1000,1);
d = filt(x) + n;

適応フィルター

正規化された LMS アルゴリズムのバリエーションを使用するには、dsp.LMSFilter の Method プロパティを 'Normalized LMS' に設定します。適応フィルターの長さを 13 タップ、ステップ サイズを 0.2 に設定します。

mu = 0.2;
lms = dsp.LMSFilter(13,'StepSize',mu,'Method',...
   'Normalized LMS');

一次入力信号 x と目的の信号 d を LMS フィルターに渡します。

[y,e,w] = lms(x,d);

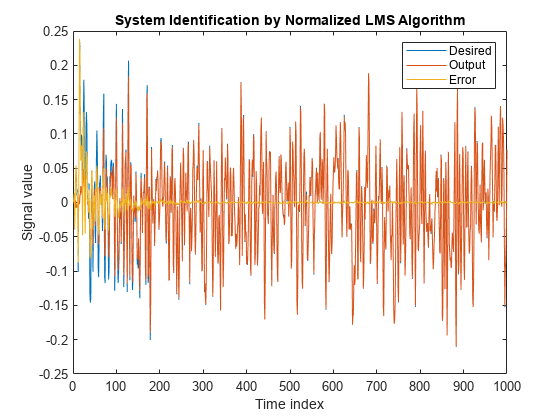
適応フィルターの出力 y は目的の信号 d に収束された信号であり、2 つの信号間の誤差 e を最小化します。

plot(1:1000, [d,y,e])
title('System Identification by Normalized LMS Algorithm')
legend('Desired','Output','Error')
xlabel('Time index')
ylabel('Signal value')

適応させたフィルターと未知のシステムとの比較

重みベクトル w は、未知のシステム (FIR フィルター) に似るように適応させた LMS フィルターの係数を表します。収束を確認するために、FIR フィルターの分子係数と適応フィルターの推定された重み付けを比較します。

stem([(filt.Numerator).' w])
title('System Identification by Normalized LMS Algorithm')
legend('Actual filter weights','Estimated filter weights',...
       'Location','NorthEast')

LMS アルゴリズムと正規化 LMS アルゴリズムの収束性能の比較

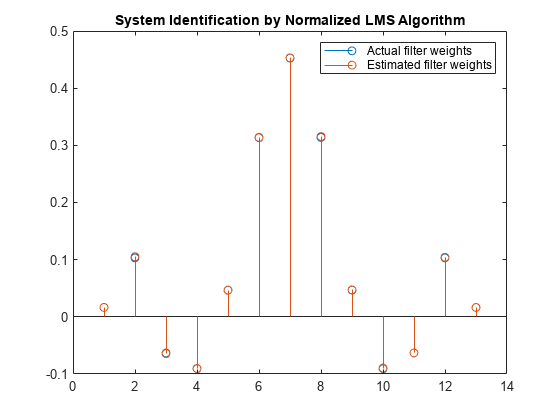
適応フィルターは、未知のシステムの係数と一致するように自身のフィルターの係数を適応させます。目的は、未知のシステムの出力と適応フィルターの出力の間で誤差信号を最小化することです。同じ入力に対して 2 つの出力が収束して非常によく一致する場合、係数は非常によく一致すると呼ばれます。この状態の適応フィルターは、未知のシステムに似ています。この例では、正規化 LMS (NLMS) アルゴリズムと正規化を行わない LMS アルゴリズムに対して、この収束が発生する速さを比較します。

未知のシステム

未知のシステムを表す dsp.FIRFilter を作成します。未知のシステムへの入力として信号 x を渡します。目的の信号 d は、未知のシステム (FIR フィルター) の出力と加法性ノイズ信号 n の和です。

filt = dsp.FIRFilter;
filt.Numerator = fircband(12,[0 0.4 0.5 1],[1 1 0 0],[1 0.2],... 
{'w' 'c'});
x = 0.1*randn(1000,1);
n = 0.001*randn(1000,1);
d = filt(x) + n;

適応フィルター

2 つの dsp.LMSFilter オブジェクトを作成し、1 つを LMS アルゴリズムに、もう 1 つを正規化 LMS アルゴリズムに設定します。適応ステップ サイズとして 0.2 を選択し、適応フィルターの長さを 13 タップに設定します。

mu = 0.2;
lms_nonnormalized = dsp.LMSFilter(13,'StepSize',mu,...
    'Method','LMS');
lms_normalized = dsp.LMSFilter(13,'StepSize',mu,...
    'Method','Normalized LMS');

一次入力信号 x と目的の信号 d を両方の LMS アルゴリズムのバリエーションに渡します。変数 e1 および e2 はそれぞれ、目的の信号と正規化されたフィルターの出力の間の誤差、および目的の信号と正規化されていないフィルターの出力の間の誤差を表します。

[~,e1,~] = lms_normalized(x,d);
[~,e2,~] = lms_nonnormalized(x,d);

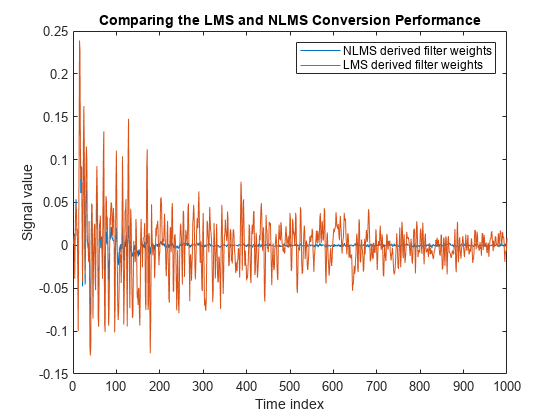
両方のバリエーションについて誤差信号をプロットします。NLMS バリアントの誤差信号は、LMS バリアントの誤差信号よりはるかに速くゼロに収束します。正規化されたバージョンは、はるかに少ない反復回数で、正規化されていないバージョンと同じ程度に良好な結果に適応します。

plot([e1,e2]);
title('Comparing the LMS and NLMS Conversion Performance');
legend('NLMS derived filter weights', ...
       'LMS derived filter weights','Location', 'NorthEast');
xlabel('Time index')
ylabel('Signal value')

LMS フィルターを使用したノイズの打ち消し

LMS 適応フィルターを使用して未知のシステムに追加された加法性ノイズ n を打ち消します。LMS フィルターは、その伝達関数が未知のシステムの伝達関数と可能な限り一致するまでその係数を調整します。適応フィルターの出力と未知のシステムの出力間の差異は、誤差信号 e を意味します。この誤差信号の最小化が適応フィルターの目的です。

未知のシステムと LMS フィルターは、同じ入力信号 x を処理し、出力 d と y をそれぞれ生成します。適応フィルターの係数が未知のシステムの係数と一致する場合、誤差 e は実際は加法性ノイズを意味します。

メモ: R2016a 以前のリリースを使用している場合、それぞれのオブジェクトの呼び出しを等価な step 構文で置き換えてください。たとえば、obj(x) は step(obj,x) になります。

未知のシステムを表す dsp.FIRFilter System object を作成します。dsp.LMSFilter オブジェクトを作成し、長さを 11 タップ、ステップ サイズを 0.05 に設定します。未知のシステムに追加されたノイズを表す正弦波を作成します。時間スコープに信号が表示されます。

FrameSize = 100;
NIter = 10;
lmsfilt2 = dsp.LMSFilter('Length',11,'Method','Normalized LMS', ...
    'StepSize',0.05);
firfilt2 = dsp.FIRFilter('Numerator', fir1(10,[.5, .75]));
sinewave = dsp.SineWave('Frequency',0.01, ...
    'SampleRate',1,'SamplesPerFrame',FrameSize);
scope = timescope('TimeUnits','Seconds',...
    'YLimits',[-3 3],'BufferLength',2*FrameSize*NIter, ...
    'ShowLegend',true,'ChannelNames', ...
    {'Noisy signal', 'Error signal'});

ランダムな入力信号 x を作成し、信号を FIR フィルターに渡します。正弦波を FIR フィルターの出力に追加し、ノイズを含む信号 d を生成します。信号 d は未知のシステムの出力です。ノイズを含む信号と一次入力信号を LMS フィルターに渡します。ノイズを含む信号と誤差信号を時間スコープで表示します。

for k = 1:NIter
    x = randn(FrameSize,1);
    d = firfilt2(x) + sinewave();
    [y,e,w] = lmsfilt2(x,d);
    scope([d,e])
end
release(scope)

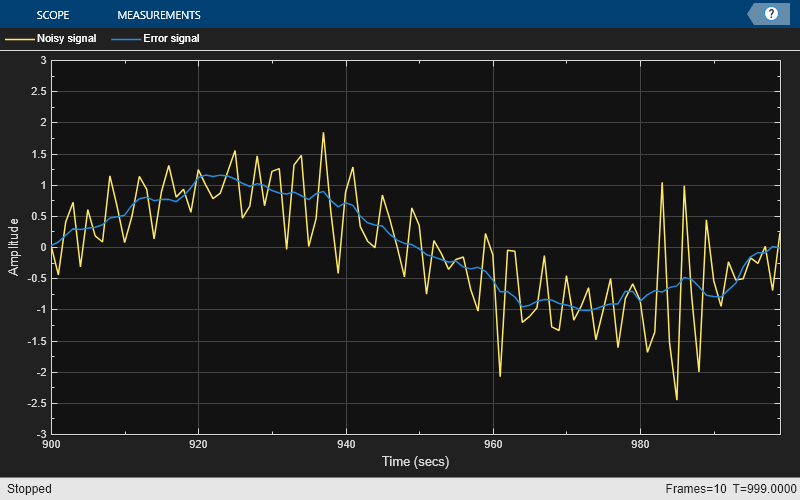
誤差信号 e は未知のシステムに追加された正弦波ノイズです。誤差信号の最小化によりシステムに追加されたノイズが最小化されます。

符号-データ LMS アルゴリズムを使用したノイズ キャンセリング

適応フィルターを導き出すために必要な計算量が開発プロセスに影響を与える場合、この例で示すように、LMS アルゴリズムの符号-データ バリアント (SDLMS) は優れた選択肢となる可能性があります。

LMS 適応フィルターの標準および正規化された変動において、適応フィルターの係数は目的の信号と未知のシステムからの出力信号間の平均二乗誤差より発生します。符号-データ アルゴリズムでは、入力データの符号を使用してフィルター係数を変更することにより、平均二乗誤差の計算が変更されます。

誤差が正である場合、新しい係数は、誤差にステップ サイズ µ を乗算して前の係数に加算した値になります。誤差が負である場合、新しい係数は、誤差に µ を乗算して前の係数から減算した値になります。符号の変化に注意してください。

入力がゼロの場合、新しい係数は前のセットと同じです。

ベクトル形式では、符号-データ LMS アルゴリズムは次のようになります。

$$\mathit{w}\left(\mathit{k}+1\right)=\mathit{w}\left(\mathit{k}\right)+\mu \mathit{e}\left(\mathit{k}\right)\mathrm{sgn}\left(\mathit{x}\left(\mathit{k}\right)\right),$$

ここで、

$$\mathrm{sgn}\left(\mathit{x}\left(\mathit{k}\right)\right)=\{\begin{array}{c}1,\mathit{x}\left(\mathit{k}\right)>0\\ 0,\mathit{x}\left(\mathit{k}\right)=0\\ -1,\mathit{x}\left(\mathit{k}\right)<0\end{array}$$

ベクトル $\mathit{w}$ はフィルターの係数に適用された重み、ベクトル $\mathit{x}$ は入力データです。ベクトル $\mathit{e}$ は、目的の信号とフィルターを適用した信号の間の誤差です。SDLMS アルゴリズムの目的は、この誤差を最小化することです。ステップ サイズは、$\mu$ によって表されます。

$\mu$ を小さくすると、フィルターの重みに対する補正が各サンプルについて小さくなり、SDLMS の誤差がより緩やかに小さくなります。$\mu$ を大きくすると、各ステップの重みがより大きく変化するので、誤差がより高速に小さくなりますが、生成される誤差は理想的な解にはあまり近づきません。優れた収束速度と安定性を確保するには、次の実用的な範囲内で $\mu$ を選択します。

$$0<\mu <\frac{1}{\mathit{N}\left\{\mathrm{InputSignalPower}\right\}},$$

ここで、$\mathit{N}$ は信号のサンプル数です。また、効率的に計算するために $\mu$ を 2 のべき乗として定義します。

メモ: 符号-データ アルゴリズムの初期条件をどのように設定するかは適応処理の効果に大きく影響します。アルゴリズムは基本的に入力信号を量子化するため、アルゴリズムは簡単に不安定になる可能性があります。

一連の大きな入力値を量子化プロセスと組み合わせると、誤差がすべての範囲を超えて大きくなる可能性があります。小さいステップ サイズ $\left(\mu \ll 1\right)$ を選択し、アルゴリズムの初期条件を非ゼロの正および負の値に設定することにより、制御できなくなるという符号-データ アルゴリズムの傾向を制限します。

このノイズ キャンセリングの例では、dsp.LMSFilter の Method プロパティを 'Sign-Data LMS' に設定します。この例には、2 つの入力データセットが必要です。

• ノイズによって破損した信号が含まれるデータ。ノイズまたは干渉の除去 –– 適応フィルターを使用した、未知のシステムからのノイズの除去のブロック線図では、これは目的の信号 $\mathit{d}\left(\mathit{k}\right)$ です。ノイズ キャンセリング プロセスでは、信号からノイズが除去されます。

• ランダム ノイズが含まれているデータ。ノイズまたは干渉の除去 –– 適応フィルターを使用した、未知のシステムからのノイズの除去のブロック線図では、これは $\mathit{x}\left(\mathit{k}\right)$ です。信号 $\mathit{x}\left(\mathit{k}\right)$ は、信号データを破損するノイズに関連します。ノイズ データ間の相関がないと、適応アルゴリズムで信号からノイズを除去できません。

信号には、正弦波を使用します。signal は 1000 要素の列ベクトルであることに注意してください。

signal = sin(2*pi*0.055*(0:1000-1)');

今度は、相関ホワイト ノイズを signal に追加します。ノイズが相関していることを確認するには、ローパス FIR フィルターを介してノイズを渡してから、フィルター処理されたノイズを信号に追加します。

noise = randn(1000,1);
filt = dsp.FIRFilter;
filt.Numerator = fir1(11,0.4);
fnoise = filt(noise);
d = signal + fnoise;

fnoise は相関ノイズであり、d は符号-データ アルゴリズムに対する目的の信号になります。

dsp.LMSFilter オブジェクトを処理用に準備するには、フィルターの重みの初期条件と mu (StepSize) を設定します。この節で前述したように、coeffs と mu に設定する値によって適応フィルターが信号パスからノイズを除去できるかどうかが決まります。

LMS アルゴリズムの使用による FIR フィルターのシステム同定では、フィルター係数をゼロに設定する既定のフィルターを作成しました。ほとんどの場合、この方法は符号-データ アルゴリズムで機能しません。設定する初期フィルター係数が期待値に近いほどアルゴリズムは適切に機能し、効果的にノイズを除去するフィルターの解に収束します。

この例では、ノイズ フィルターで使用する係数 (filt.Numerator) から開始して、アルゴリズムが適応しなければならないように若干変更します。

coeffs = (filt.Numerator).'-0.01; % Set the filter initial conditions.
mu = 0.05; % Set the step size for algorithm updating.

dsp.LMSFilter に必要な入力引数を準備したら、LMS フィルター オブジェクトを作成し、適応を実行して、結果を表示します。

lms = dsp.LMSFilter(12,'Method','Sign-Data LMS',...
   'StepSize',mu,'InitialConditions',coeffs);
[~,e] = lms(noise,d);
L = 200;
plot(0:L-1,signal(1:L),0:L-1,e(1:L));
title('Noise Cancellation by the Sign-Data Algorithm');
legend('Actual signal','Result of noise cancellation',...
       'Location','NorthEast');
xlabel('Time index')
ylabel('Signal values')

dsp.LMSFilter を実行すると、いずれの標準 LMS アルゴリズムよりもはるかに少ない乗算演算が使用されます。また、ステップ サイズが 2 のべき乗の場合、ビット シフトによる乗算だけで符号-データ適応を実行できます。

符号-データ アルゴリズムの性能はこのプロットに示すように非常に良好ですが、符号-データ アルゴリズムは標準 LMS の変動より安定性がかなり低下します。このノイズ キャンセリング例で、処理後の信号は入力信号と非常によく一致しますが、アルゴリズムは優れた性能を実現するのではなく、とても簡単に制限なく拡大します。

重みの初期条件 (InitialConditions) と mu (StepSize)、または相関ノイズの作成に使用したローパス フィルターを変更すると、ノイズ キャンセリングが失敗します。

符号-誤差 LMS アルゴリズムを使用したノイズ キャンセリング

LMS 適応フィルターの標準および正規化された変動において、適応フィルターの係数は目的の信号と未知のシステムからの出力信号間の平均二乗誤差を計算し、その結果を現在のフィルター係数に適用することにより発生します。符号-誤差 LMS アルゴリズム (SELMS) は、誤差の符号を使用することで平均二乗誤差の計算を置き換え、フィルター係数を変更します。

誤差が正である場合、新しい係数は、誤差にステップ サイズ $\mu$ を乗算して前の係数に加算した値になります。誤差が負である場合、新しい係数は、誤差に $\mu$ を乗算して前の係数から減算した値になります。符号の変化に注意してください。入力がゼロの場合、新しい係数は前のセットと同じです。

ベクトル形式の場合、符号-誤差 LMS アルゴリズムは次のようになります。

$\mathit{w}\left(\mathit{k}+1\right)=\mathit{w}\left(\mathit{k}\right)+\mu \mathrm{sgn}\left(\mathit{e}\left(\mathit{k}\right)\right)\left(\mathit{x}\left(\mathit{k}\right)\right)$,

ここで、

$$\mathrm{sgn}\left(\mathit{e}\left(\mathit{k}\right)\right)=\{\begin{array}{c}1,\mathit{e}\left(\mathit{k}\right)>0\\ 0,\mathit{e}\left(\mathit{k}\right)=0\\ -1,\mathit{e}\left(\mathit{k}\right)<0\end{array}$$

ベクトル $\mathit{w}$ はフィルターの係数に適用された重み、ベクトル $\mathit{x}$ は入力データです。ベクトル $\mathit{e}$ は、目的の信号とフィルターを適用した信号の間の誤差です。SELMS アルゴリズムの目的は、この誤差を最小化することです。

$\mu$ を小さくすると、フィルターの重みに対する補正が各サンプルについて小さくなり、SELMS の誤差がより緩やかに小さくなります。$\mu$ を大きくすると、各ステップの重みがより大きく変化するので、誤差がより高速に小さくなりますが、生成される誤差は理想的な解にはあまり近づきません。優れた収束速度と安定性を確保するには、次の実用的な範囲内で $\mu$ を選択します。

$$0<\mu <\frac{1}{\mathit{N}\left\{\mathrm{InputSignalPower}\right\}}$$

ここで、$\mathit{N}$ は信号のサンプル数です。また、効率的に計算するために $\mu$ を 2 のべき乗として定義します。

メモ: 符号-誤差アルゴリズムの初期条件をどのように設定するかは適応処理の効果に大きく影響します。アルゴリズムは基本的に誤差信号を量子化するため、アルゴリズムは簡単に不安定になる可能性があります。

一連の大きな誤差値を量子化プロセスと組み合わせると、誤差がすべての範囲を超えて大きくなる可能性があります。小さいステップ サイズ $\left(\mu \ll 1\right)$ を選択し、アルゴリズムの初期条件を非ゼロの正および負の値に設定することにより、不安定になるという符号-誤差アルゴリズムの傾向を制限します。

このノイズ キャンセリングの例では、dsp.LMSFilter の Method プロパティを 'Sign-Error LMS' に設定します。この例には、2 つの入力データセットが必要です。

• ノイズによって破損した信号が含まれるデータ。ノイズまたは干渉の除去 –– 適応フィルターを使用した、未知のシステムからのノイズの除去のブロック線図では、これは目的の信号 $\mathit{d}\left(\mathit{k}\right)$ です。ノイズ キャンセリング プロセスでは、信号からノイズが除去されます。

• ランダム ノイズが含まれているデータ。ノイズまたは干渉の除去 –– 適応フィルターを使用した、未知のシステムからのノイズの除去のブロック線図では、これは $\mathit{x}\left(\mathit{k}\right)$ です。信号 $\mathit{x}\left(\mathit{k}\right)$ は、信号データを破損するノイズに関連します。ノイズ データ間の相関がないと、適応アルゴリズムで信号からノイズを除去できません。

信号には、正弦波を使用します。signal は 1000 要素の列ベクトルであることに注意してください。

signal = sin(2*pi*0.055*(0:1000-1)');

今度は、相関ホワイト ノイズを signal に追加します。ノイズが相関していることを確認するには、ローパス FIR フィルターを介してノイズを渡してから、フィルター処理されたノイズを信号に追加します。

noise = randn(1000,1);
filt = dsp.FIRFilter;
filt.Numerator = fir1(11,0.4);
fnoise = filt(noise);
d = signal + fnoise;

fnoise は関連付けられたノイズであり、d は符号-誤差アルゴリズムに対する目的の入力になります。

dsp.LMSFilter オブジェクトを処理用に準備するには、フィルターの重み (InitialConditions) の初期条件と mu (StepSize) を設定します。この節で前述したように、coeffs と mu に設定する値によって適応フィルターが信号パスからノイズを除去できるかどうかが決まります。

LMS アルゴリズムの使用による FIR フィルターのシステム同定では、フィルター係数をゼロに設定する既定のフィルターを作成しました。ほとんどの場合、この方法は符号-誤差アルゴリズムで機能しません。設定する初期フィルター係数が期待値に近いほどアルゴリズムは適切に機能し、効果的にノイズを除去するフィルターの解に収束します。

この例では、ノイズ フィルターで使用する係数 (filt.Numerator) から開始して、アルゴリズムが適応しなければならないように若干変更します。

coeffs = (filt.Numerator).'-0.01; % Set the filter initial conditions.
mu = 0.05; % Set the step size for algorithm updating.

dsp.LMSFilter に必要な入力引数を準備したら、適応を実行して、結果を表示します。

lms = dsp.LMSFilter(12,'Method','Sign-Error LMS',...
   'StepSize',mu,'InitialConditions',coeffs);
[~,e] = lms(noise,d);
L = 200;
plot(0:199,signal(1:200),0:199,e(1:200));
title('Noise cancellation performance by the sign-error LMS algorithm');
legend('Actual signal','Error after noise reduction',...
       'Location','NorthEast')
xlabel('Time index')
ylabel('Signal value')

符号-誤差 LMS アルゴリズムを実行すると、いずれの標準 LMS アルゴリズムよりもはるかに少ない乗算演算が使用されます。また、ステップ サイズが 2 のべき乗の場合、ビット シフトによる乗算だけで符号-誤差適応を実行できます。

符号-誤差アルゴリズムは、このプロットに示すように非常に良好な性能ですが、標準 LMS のバリエーションより安定性がかなり低下します。このノイズ キャンセリング例で、適応後の信号は入力信号と非常によく一致しますが、アルゴリズムは優れた性能を実現するのではなく、とても簡単に不安定になります。

重みの初期条件 (InitialConditions) と mu (StepSize)、または相関ノイズの作成に使用したローパス フィルターを変更すると、ノイズ キャンセリングが失敗し、アルゴリズムが役に立たなくなります。

符号-符号 LMS アルゴリズムを使用したノイズ キャンセリング

符号-符号 LMS アルゴリズム (SSLMS) では、入力データの符号を使用して平均二乗誤差の計算を置き換え、フィルター係数を変更します。誤差が正である場合、新しい係数は、誤差にステップ サイズ $\mu$ を乗算して前の係数に加算した値になります。誤差が負である場合、新しい係数は、誤差に $\mu$ を乗算して前の係数から減算した値になります。符号の変化に注意してください。入力がゼロの場合、新しい係数は前のセットと同じです。

基本的に、アルゴリズムは誤差と入力の両方を符号演算子を適用して量子化します。

ベクトル形式の場合、符号-符号 LMS アルゴリズムは次のようになります。

$$w(k+1)=w\left(k\right)+\mu \mathrm{sgn}\left(e\left(k\right)\right)\mathrm{sgn}\left(x\left(k\right)\right),$$

ここで、

$$\mathrm{sgn}\left(\mathit{z}\left(\mathit{k}\right)\right)=\{\begin{array}{c}1,\mathit{z}\left(\mathit{k}\right)>0\\ 0,\mathit{z}\left(\mathit{k}\right)=0\\ -1,\mathit{z}\left(\mathit{k}\right)<0\end{array}$$

$$\mathit{z}\left(\mathit{k}\right)=\mathit{e}\left(\mathit{k}\right)\mathrm{sgn}\left(\mathit{x}\left(\mathit{k}\right)\right)$$

ベクトル $\mathit{w}$ はフィルターの係数に適用された重み、ベクトル $\mathit{x}$ は入力データです。ベクトル $\mathit{e}$ は、目的の信号とフィルターを適用した信号の間の誤差です。SSLMS アルゴリズムの目的は、この誤差を最小化することです。

$\mu$ を小さくすると、フィルターの重みに対する補正が各サンプルについて小さくなり、SSLMS の誤差がより緩やかに小さくなります。$\mu$ を大きくすると、各ステップの重みがより大きく変化するので、誤差がより高速に小さくなりますが、生成される誤差は理想的な解にはあまり近づきません。優れた収束速度と安定性を確保するには、次の実用的な範囲内で $\mu$ を選択します。

$$0<\mu <\frac{1}{\mathit{N}\left\{\mathrm{InputSignalPower}\right\}}$$

ここで、$\mathit{N}$ は信号のサンプル数です。また、効率的に計算するために $\mu$ を 2 のべき乗として定義します。

メモ:

符号-符号アルゴリズムの初期条件をどのように設定するかは適応処理の効果に大きく影響します。アルゴリズムは基本的に入力信号と誤差信号を量子化するため、アルゴリズムは簡単に不安定になる可能性があります。

一連の大きな誤差値を量子化プロセスと組み合わせると、誤差がすべての範囲を超えて大きくなる可能性があります。小さいステップ サイズ $\left(\mu \ll 1\right)$ を選択し、アルゴリズムの初期条件を非ゼロの正および負の値に設定することにより、不安定になるという符号-符号アルゴリズムの傾向を制限します。

このノイズ キャンセリングの例では、dsp.LMSFilter の Method プロパティを 'Sign-Sign LMS' に設定します。この例には、2 つの入力データセットが必要です。

• ノイズによって破損した信号が含まれるデータ。ノイズまたは干渉の除去 –– 適応フィルターを使用した、未知のシステムからのノイズの除去のブロック線図では、これは目的の信号 $\mathit{d}\left(\mathit{k}\right)$ です。ノイズ キャンセリング プロセスでは、信号からノイズが除去されます。

• ランダム ノイズが含まれているデータ。ノイズまたは干渉の除去 –– 適応フィルターを使用した、未知のシステムからのノイズの除去のブロック線図では、これは $\mathit{x}\left(\mathit{k}\right)$ です。信号 $\mathit{x}\left(\mathit{k}\right)$ は、信号データを破損するノイズに関連します。ノイズ データ間の相関がないと、適応アルゴリズムで信号からノイズを除去できません。

信号には、正弦波を使用します。signal は 1000 要素の列ベクトルであることに注意してください。

signal = sin(2*pi*0.055*(0:1000-1)');

今度は、相関ホワイト ノイズを signal に追加します。ノイズが相関していることを確認するには、ローパス FIR フィルターを介してノイズを渡してから、フィルター処理されたノイズを信号に追加します。

noise = randn(1000,1);
filt = dsp.FIRFilter;
filt.Numerator = fir1(11,0.4);
fnoise = filt(noise);
d = signal + fnoise;

fnoise は関連付けられたノイズであり、d は符号-符号アルゴリズムに対する目的の入力になります。

dsp.LMSFilter オブジェクトを処理用に準備するには、フィルターの重み (InitialConditions) の初期条件と mu (StepSize) を設定します。この節で前述したように、coeffs と mu に設定する値によって適応フィルターが信号パスからノイズを除去できるかどうかが決まります。LMS アルゴリズムの使用による FIR フィルターのシステム同定では、フィルター係数をゼロに設定する既定のフィルターを作成しました。通常、この方法は符号-符号アルゴリズムで機能しません。

設定する初期フィルター係数が期待値に近いほどアルゴリズムは適切に機能し、効果的にノイズを除去するフィルターの解に収束します。この例では、ノイズ フィルターで使用する係数 (filt.Numerator) から開始して、アルゴリズムが適応するように少し変更します。

coeffs = (filt.Numerator).' -0.01; % Set the filter initial conditions.
mu = 0.05;

dsp.LMSFilter に必要な入力引数を準備したら、適応を実行して、結果を表示します。

lms = dsp.LMSFilter(12,'Method','Sign-Sign LMS',...
   'StepSize',mu,'InitialConditions',coeffs);
[~,e] = lms(noise,d);
L = 200;
plot(0:199,signal(1:200),0:199,e(1:200));
title('Noise cancellation performance by the sign-sign LMS algorithm');
legend('Actual signal','Error after noise reduction',...
       'Location','NorthEast')
xlabel('Time index')
ylabel('Signal value')

dsp.LMSFilter を実行すると、いずれの標準 LMS アルゴリズムよりもはるかに少ない乗算演算が使用されます。また、符号-符号適応を実行するには、ステップ サイズが 2 のべき乗のときにのみ乗算するビット シフトが必要です。

符号-符号アルゴリズムは、このプロットに示すように非常に良好な性能ですが、標準 LMS のバリエーションより安定性がかなり低下します。このノイズ キャンセリング例で、適応後の信号は入力信号と非常によく一致しますが、アルゴリズムは優れた性能を実現するのではなく、とても簡単に不安定になります。

重みの初期条件 (InitialConditions) と mu (StepSize)、または相関ノイズの作成に使用したローパス フィルターを変更すると、ノイズ キャンセリングが失敗し、アルゴリズムが役に立たなくなります。

LMS フィルターの重みの完全な履歴へのアクセス

メモ: この例は R2017a 以降でのみ動作します。R2017a より前のリリースを使用している場合、このオブジェクトでフィルターの重みのサンプルごとの完全な履歴は出力されません。R2016b より以前のリリースを使用している場合は、それぞれの関数の呼び出しを等価な step 構文で置き換えてください。たとえば、myObject(x) は step(myObject,x) になります。

dsp.LMSFilter System object を初期化し、WeightsOutput プロパティを 'All' に設定します。この設定により、LMS フィルターで次元 [FrameLength Length] の重みの行列の出力が有効になり、入力値の FrameLength 個のすべてのサンプルについて、サンプルごとの重みの完全な履歴が出力されるようになります。

FrameSize = 15000;
lmsfilt3 = dsp.LMSFilter('Length',63,'Method','LMS', ...
    'StepSize',0.001,'LeakageFactor',0.99999, ...
    'WeightsOutput','All'); % full Weights history

w_actual = fir1(64,[0.5 0.75]);
firfilt3 = dsp.FIRFilter('Numerator',w_actual);
sinewave = dsp.SineWave('Frequency',0.01, ...
    'SampleRate',1,'SamplesPerFrame',FrameSize);

scope = timescope('TimeUnits','Seconds', ...
    'YLimits',[-0.25 0.75],'BufferLength',2*FrameSize, ...
    'ShowLegend',true,'ChannelNames', ...
    {'Coeff 33 Estimate','Coeff 34 Estimate','Coeff 35 Estimate', ...
    'Coeff 33 Actual','Coeff 34 Actual','Coeff 35 Actual'});

1 つのフレームを実行し、適応重みの完全な履歴 w を出力します。

x = randn(FrameSize,1);       % Input signal
d = firfilt3(x) + sinewave(); % Noise + Signal
[~,~,w] = lmsfilt3(x,d);

w の各行は、それぞれの入力サンプルについて推定された一連の重みです。w の各列に特定の重みの完全な履歴が格納されます。33、34、35 番目の実際の重みと完全な履歴をプロットします。プロットでは、適応フィルターが入力サンプルの受信と適応を継続するにつれ、推定される重みの出力が結果的に実際の重みに収束することを確認できます。

idxBeg = 33;
idxEnd = 35;
scope([w(:,idxBeg:idxEnd), repmat(w_actual(idxBeg:idxEnd),FrameSize,1)])

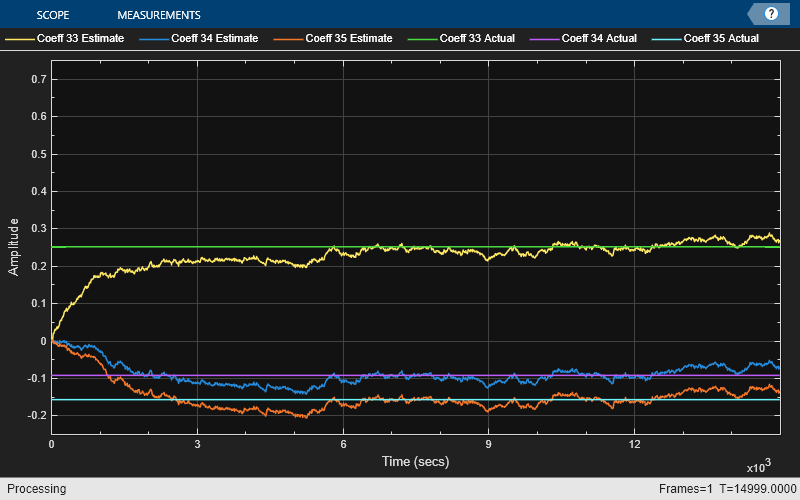
詳細

固定小数点

次の図は、dsp.LMSFilter オブジェクト内で固定小数点信号に使用されるデータ型を示します。次の表は図で使用されている変数の定義をまとめています。

変数	定義
u	入力ベクトル
W	フィルターの重みのベクトル
µ	ステップ サイズ
e	エラー
Q	商、$$Q=\frac{\mu \cdot e}{u\text{'}u}$$
積 u'u	エネルギー計算の図における積のデータ型
アキュムレータ u'u	エネルギー計算の図におけるアキュムレータのデータ型
積 W'u	畳み込みの図における積のデータ型
アキュムレータ W'u	畳み込みの図におけるアキュムレータのデータ型
積 $$\mu \cdot e$$	ステップ サイズと誤差の積の図における積のデータ型
積 $$Q\cdot u$$	重みの更新の図における積とアキュムレータのデータ型1

¹この量のアキュムレータのデータ型は、積のデータ型と同じになるように自動的に設定されます。このアキュムレータの最小、最大およびオーバーフロー情報は積の情報の一部としてログ記録されます。オートスケーリングは、この積とアキュムレータを 1 つのデータ型として扱います。

System object プロパティに、プロパティのデータ型、重み、積、商、アキュムレータを設定できます。固定小数点の入出力および System object プロパティは次の特性をもたなければなりません。

• 入力信号と目的の信号は同じ語長でなければならないが、その小数部の長さは異なってもよい。

• ステップ サイズと漏れ係数は同じ語長でなければならないが、その小数部の長さは異なってもよい。

• 出力信号と誤差信号は目的の信号と同じ語長と小数部の長さをもっている。

• u'u、W'u、$$\mu \cdot e$$ および $$Q\cdot u$$ の演算の商と積の出力は同じ語長でなければならないが、その小数部の長さは異なってもよい。

• u'u および W'u の演算のアキュムレータのデータ型は同じ語長でなければならないが、その小数部の長さは異なってもよい。

乗算器への入力の少なくとも 1 つが実数の場合、乗算器の出力は積の出力データ型になります。乗算器への入力が両方とも複素数の場合、乗算の結果はアキュムレータのデータ型になります。実行される複素数の乗算の詳細については、乗算のデータ型を参照してください。

アルゴリズム

LMS フィルターのアルゴリズムは次の方程式で定義されます。

$$\begin{array}{c}y(n)=w^T(n-1)u(n)\\ e(n)=d(n)-y(n)\\ w(n)=\alpha w(n-1)+f(u(n),e(n),\mu )\end{array}$$

この System object で使用できるさまざまな LMS 適応フィルター アルゴリズムは、次のように定義されます。

• LMS –– Wiener-Hopf 方程式を解き、適応フィルターのフィルター係数を求めます。

  $$f(u(n),e(n),\mu )=\mu e(n)u^{*}(n)$$

• 正規化 LMS –– 正規化された LMS アルゴリズムのバリエーション。

  $$f(u(n),e(n),\mu )=\mu e(n)\frac{u^{\ast }(n)}{\epsilon +u^H(n)u(n)}$$

  正規化された LMS では、重みの更新時に数値が不安定になる可能性を克服するため、小さい正の定数 ε が分母に追加されました。倍精度浮動小数点入力の場合、ε は関数 eps の出力です。単精度浮動小数点入力の場合、ε は eps("single") の出力です。固定小数点入力の場合、ε は 0 です。

• 符号-データ LMS –– 各反復におけるフィルターの重みに対する補正が、入力 u(n) の符号に依存します。

  $$f(u(n),e(n),\mu )=\mu e(n)\text{sign}(u(n))$$

  u(n) は実数です。

• 符号-誤差 LMS –– 連続する各反復に対する現在のフィルターの重みに適用される補正が、誤差 e(n) の符号に依存します。

  $$f(u(n),e(n),\mu )=\mu \text{sign}(e(n))u^{*}(n)$$

• 符号-符号 LMS –– 連続する各反復に対する現在のフィルターの重みに適用される補正が、u(n) の符号と e(n) の符号の両方に依存します。

  $$f(u(n),e(n),\mu )=\mu \text{sign}(e(n))\text{sign}(u(n))$$

  u(n) は実数です。

変数は次のようになります。

変数	説明
n	現在の時間インデックス
u(n)	ステップ n でのバッファー済み入力サンプルのベクトル
u*(n)	ステップ n でのバッファー済み入力サンプルのベクトルの複素共役
w(n)	ステップ n でのフィルターの重み推定ベクトル
y(n)	ステップ n でのフィルター処理された出力
e(n)	ステップ n での推定誤差
d(n)	ステップ n での目的の応答
µ	適応ステップ サイズ
α	漏れ係数 (0 < α ≤ 1)
ε	重みの更新時に数値が不安定になる可能性を修正する定数。

参照

[1] Hayes, M.H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

MATLAB コード生成における System object (MATLAB Coder)を参照してください。

dsp.LMSFilter System object は、次の条件下で Intel AVX2 テクノロジーを使用した SIMD コード生成をサポートします。

• Method が 'LMS' または 'Normalized LMS' に設定されている。

• WeightsOutput が 'None' または 'Last' に設定されている。

• 入力信号が実数値である。

• 入力信号のデータ型が single または double である。

SIMD テクノロジーにより、生成コードのパフォーマンスが大幅に向上します。

バージョン履歴

R2012a で導入

参考

関数

• msepred | msesim | maxstep

オブジェクト

• dsp.BlockLMSFilter | dsp.FIRFilter | dsp.FilteredXLMSFilter | dsp.FrequencyDomainAdaptiveFilter | dsp.AdaptiveLatticeFilter | dsp.AffineProjectionFilter | dsp.FastTransversalFilter | dsp.RLSFilter

ブロック

• LMS Filter | LMS Update

トピック

• 適応フィルターとアプリケーションの概要
• Signal Enhancement Using LMS and NLMS Algorithms
• Variable-Size Signal Support DSP System Objects

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい