このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
dsp.RLSFilter
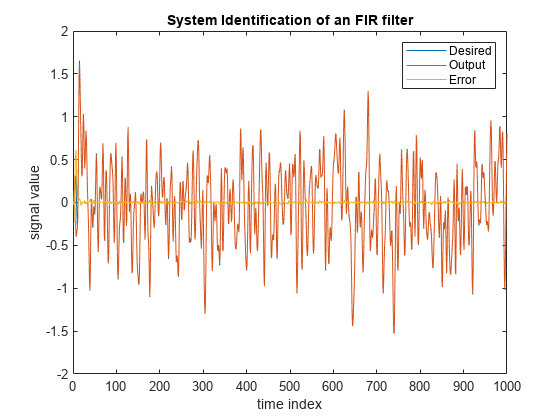
R2026a再帰的最小二乗 (RLS) アルゴリズムを使用した出力、誤差および係数の計算
説明
dsp.RLSFilter System object™ は、RLS フィルターの実装を使用して入力の各チャネルをフィルター処理します。
入力の各チャネルをフィルターするには、次を実行します。
dsp.RLSFilterオブジェクトを作成し、そのプロパティを設定します。関数と同様に、引数を指定してオブジェクトを呼び出します。
System object の機能の詳細については、System object とはを参照してください。
作成
説明
rlsFilt = dsp.RLSFilterrlsFilt を返します。この System object は、RLS アルゴリズムを使用して、フィルター済み出力、フィルター誤差および指定の入力と目的の信号に対するフィルターの重みを計算します。
rlsFilt = dsp.RLSFilter(len)rlsFilt を返します。この System object には、len に設定された Length プロパティがあります。
rlsFilt = dsp.RLSFilter(PropertyName,Value)
プロパティ
使用法
説明
入力引数
出力引数
オブジェクト関数
オブジェクト関数を使用するには、System object を最初の入力引数として指定します。たとえば、obj という名前の System object のシステム リソースを解放するには、次の構文を使用します。
release(obj)
例
RLS (再帰的最小二乗) フィルターを使用してローパス FIR フィルターでモデル化した未知のシステムを同定します。未知のシステムと推定システムの周波数応答を比較します。
初期化
同定対象のシステムを表す dsp.FIRFilter オブジェクトを作成します。信号 x を FIR フィルターに渡します。未知のシステムの出力は、未知のシステム (FIR フィルター) の出力と加法性ノイズ信号 n の和である、目的の信号 d です。
filt = dsp.FIRFilter('Numerator',designLowpassFIR(FilterOrder=10,CutoffFrequency=.25));
x = randn(1000,1);
n = 0.01*randn(1000,1);
d = filt(x) + n;適応フィルター
dsp.RLSFilter オブジェクトを作成して、RLS フィルターを作成します。フィルターの長さを 11 タップに、忘却係数を 0.98 に設定します。一次入力信号 x と目的の信号 d を RLS フィルターに渡します。適応フィルターの出力 y は目的の信号 d に収束された信号であり、2 つの信号間の誤差 e を最小化します。
rls = dsp.RLSFilter(11, 'ForgettingFactor', 0.98);
[y,e] = rls(x,d);
w = rls.Coefficients;結果のプロット
出力信号と目的の信号が一致しており、これらの間の誤差はゼロに近くなっています。
plot(1:1000, [d,y,e]); title('System Identification of an FIR filter'); legend('Desired', 'Output', 'Error'); xlabel('time index'); ylabel('signal value');
重みの比較
重みベクトル w は、未知のシステム (FIR フィルター) に似るように適応させた RLS フィルターの係数を表します。収束を確認するために、FIR フィルターの分子係数と RLS フィルターの推定された重み付けを比較します。
前の信号プロットの結果を確認すると、推定されたフィルターの重みと実際のフィルターの重みがよく一致しています。
stem([filt.Numerator; w].'); legend('Actual','Estimated'); xlabel('coefficient #'); ylabel('coefficient value');
この例では、次に示す逆システム同定モデルを使用して、RLS 適応アルゴリズムの例を示します。
適応フィルターを未知のフィルターとカスケード接続すると、未知のシステムの逆数である解に適応フィルターが収束します。
未知のシステムと適応フィルターの伝達関数がそれぞれ H(z) および G(z) である場合、カスケード接続されたシステムからの信号と目的の信号の間で測定される誤差は、G(z)H(z) = 1 になるときに最小になります。この関係が成り立つには、G(z) が 1/H(z) (未知のシステムの伝達関数の逆数) に等しくなければなりません。
これが正しいことを示すため、カスケード接続されたフィルター ペアに入力する信号 s を作成します。
s = randn(3000,1);
カスケード接続されたフィルターの場合、未知のフィルターにより、両方のフィルターの後の総和点に到達する信号に遅延が発生します。まだ参照していない信号に適応フィルターが適応しようとすることを防ぐため (未来を予測することと同じです)、目的の信号を 12 サンプル遅延させます (12 は未知のシステムの次数)。
一般に、同定しようとしているシステムの次数は不明です。このような場合、適応フィルターの次数の半分に等しいサンプル数だけ目的の信号を遅延させます。入力を遅延させるには、値がゼロの 12 サンプルを入力 s に先行させる必要があります。
delay = zeros(12,1);
d = [delay; s(1:2988)]; % Concatenate the delay and the signal.目的の信号ベクトル d と x は同じ長さでなければならないので、遅延サンプルに対応するように信号要素数を調整します。
すべての場合に当てはまるわけではありませんが、この例では未知のフィルターの次数がわかっているので、未知のフィルターの次数に等しい遅延を追加します。
未知のシステムには、12 次のローパス FIR フィルターを使用します。
filt = dsp.FIRFilter; filt.Numerator = designLowpassFIR(FilterOrder=12,CutoffFrequency=0.55);
s にフィルターを適用して、適応アルゴリズム関数の入力データ信号を与えます。
x = filt(s);
RLS アルゴリズムを使用するには、dsp.RLSFilter オブジェクトを作成し、その Length、ForgettingFactor、および InitialInverseCovariance プロパティを設定します。
RLS アルゴリズムのオブジェクトを準備するための入力条件の詳細については、dsp.RLSFilterを参照してください。
p0 = 2 * eye(13); lambda = 0.99; rls = dsp.RLSFilter(13,'ForgettingFactor',lambda,... 'InitialInverseCovariance',p0);
この例では逆数の解を求めようとしているので、データを搬送する信号と目的の信号がどれであるかに注意する必要があります。
前の適応フィルターの例では、フィルターを適用したノイズを目的の信号として使用しました。このケースでは、フィルターを適用したノイズ (x) は未知のシステムの情報を搬送します。分散が 1 のガウス分布に従う、フィルターを適用しないノイズ d が目的の信号です。この適応フィルターを実行するコードは、次のようになります。
[y,e] = rls(x,d);
y には、フィルターを適用した出力が返されます。e には、未知のシステムの逆数を求めるためにフィルターが適応するときの誤差信号が格納されます。
RLS フィルターの推定係数を取得します。
b = rls.Coefficients;
freqz を使用して、適応させた RLS フィルター (逆システム、G(z)) の周波数応答を表示します。逆システムは、線形位相をもつハイパス フィルターと同じように見えます。
freqz(b,1)
未知のシステム H(z) の周波数応答を表示します。この応答は、カットオフ周波数が 0.55 であるローパス フィルターのものです。
freqz(filt.Numerator,1)
未知のシステムと適応させたフィルターをカスケード接続すると、カットオフ周波数が 0.8 に拡張された補正システムになります。
overallCoeffs = conv(filt.Numerator,b); freqz(overallCoeffs,1)
RLS 適応フィルターを使用して未知のシステムに追加された加法性ノイズ n を打ち消します。RLS フィルターは、その伝達関数が未知のシステムの伝達関数と可能な限り一致するまでその係数を調整します。適応フィルターの出力と未知のシステムの出力間の差異は、加法性ホワイト ノイズを表す誤差信号 e です。この誤差信号の最小化が適応フィルターの目的です。
初期化
未知のシステムを表す dsp.FIRFilter System object™ を作成します。dsp.RLSFilter オブジェクトを作成し、長さを 11 タップに設定します。メソッドを 'Householder RLS' に設定します。未知のシステムに追加されたノイズを表す正弦波を作成します。時間スコープに信号が表示されます。
FrameSize = 100; NIter = 10; rls = dsp.RLSFilter('Length',11,... 'Method','Householder RLS'); filt = dsp.FIRFilter('Numerator',... fir1(10,[.5,.75])); sinewave = dsp.SineWave('Frequency',0.01,... 'SampleRate',1,... 'SamplesPerFrame',FrameSize); scope = timescope('LayoutDimensions',[2 1],... 'NumInputPorts',2, ... 'TimeUnits','Seconds',... 'YLimits',[-2.5 2.5], ... 'BufferLength',2*FrameSize*NIter,... 'ActiveDisplay',1,... 'ShowLegend',true,... 'ChannelNames',{'Noisy signal'},... 'ActiveDisplay',2,... 'ShowLegend',true,... 'ChannelNames',{'Error signal'}); for k = 1:NIter x = randn(FrameSize,1); d = filt(x) + sinewave(); [y,e] = rls(x,d); w = rls.Coefficients; scope(d,e) end release(scope)
アルゴリズム
dsp.RLSFilter System object は、Conventional RLS が選択されると、FIR フィルターの重みの最小二乗推定 (RLS) を再帰的に計算します。System object は、入力信号と目的の信号に変換するために必要なフィルターの重みまたは係数を推定します。入力信号はスカラーまたは列ベクトルにすることができます。目的の信号は入力信号と同じデータ型、実数/複素数および次元をもたなければなりません。対応する RLS フィルターは、行列形式の P(n) として表現されます。
ここで、λ-1 は指数的な重み係数の逆数を示します。変数は次のようになります。
| 変数 | 説明 |
|---|---|
| n | 現在の時間インデックス |
| u(n) | ステップ n でのバッファー済み入力サンプルのベクトル |
| P(n) | ステップ n での逆相関行列の共役 |
| k(n) | ステップ n でのゲイン ベクトル |
| k*(n) | k の複素共役 |
| w(n) | ステップ n でのフィルター タップの推定ベクトル |
| y(n) | ステップ n でのフィルター処理された出力 |
| e(n) | ステップ n での推定誤差 |
| d(n) | ステップ n での目的の応答 |
| λ | 忘却係数 |
u、w、および k はすべて列ベクトルです。
参照
[1] M Hayes, Statistical Digital Signal Processing and Modeling, New York: Wiley, 1996.
[2] S. Haykin, Adaptive Filter Theory, 4th Edition, Upper Saddle River, NJ: Prentice Hall, 2002.
[3] A.A. Rontogiannis and S. Theodoridis, "Inverse factorization adaptive least-squares algorithms," Signal Processing, vol. 52, no. 1, pp. 35-47, July 1996.
[4] S.C. Douglas, "Numerically-robust O(N2) RLS algorithms using least-squares prewhitening," Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, vol. I, pp. 412-415, June 2000.
[5] A. H. Sayed, Fundamentals of Adaptive Filtering, Hoboken, NJ: John Wiley & Sons, 2003.
拡張機能
バージョン履歴
R2013a で導入
