RLS 適応フィルター処理を使用した適応ノイズ キャンセリング
この例では、RLS フィルターを使用してノイズを含む信号から有用な情報を抽出する方法を示します。情報を含む信号は、加法性ホワイト ガウス ノイズにより破損された正弦波です。
適応ノイズ キャンセリング システムでは、2 つのマイクを使用することが前提となります。メインのマイクはノイズを含む入力信号を拾い、サブのマイクは情報を含む信号に対して無相関のノイズを拾います。このノイズは、メインのマイクで拾われたノイズに相関します。
メモ: この例は、付属の Simulink® モデル rlsdemo と同じものです。
このモデルでは、ノイズを含む信号から有益な情報を抽出する適応 RLS フィルターの機能を示します。

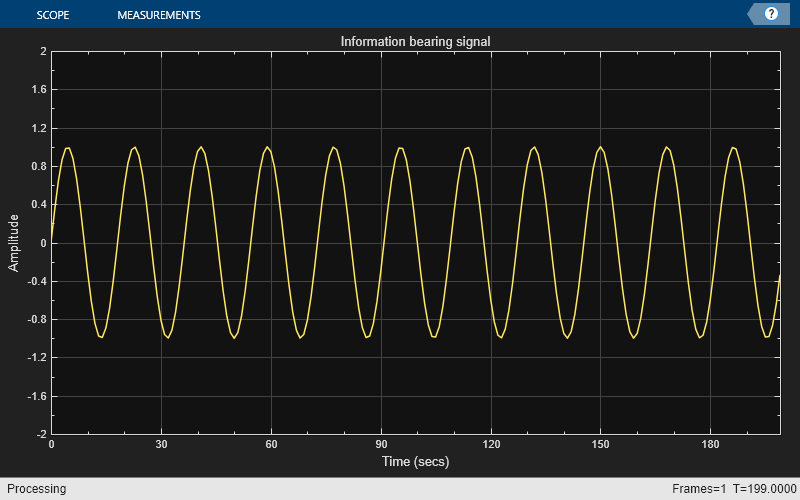
情報を含む信号は、0.055 サイクル/サンプルの正弦波です。情報を含む信号を作成し、プロットします。
signal = sin(2*pi*0.055*(0:1000-1)'); signalSource = dsp.SignalSource(signal,SamplesPerFrame=100,... SignalEndAction="Cyclic repetition"); scope = timescope(YLimits=[-2 2],Title="Information bearing signal")
scope =
timescope handle with properties:
SampleRate: 1
TimeSpanSource: 'auto'
TimeSpanOverrunAction: 'scroll'
AxesScaling: 'manual'
Show all properties
scope(signal(1:200));
サブ マイクで拾われたノイズは、RLS 適応フィルターへの入力です。正弦波を破損させるノイズは、このノイズ (と相関がある) ローパス フィルターを適用したバージョンです。フィルターされたノイズと情報を含む信号の混合信号が適応フィルターの目的の信号です。ノイズ信号を作成し、プロットします。
nvar = 1.0; % Noise variance noise = randn(1000,1)*nvar; % White noise noiseSource = dsp.SignalSource(noise,SamplesPerFrame=100,... SignalEndAction="Cyclic repetition"); scope = timescope(YLimits=[-4 4], Title="Noise picked up by the secondary microphone"); scope(noise);

情報を含む信号を破損させているノイズは、前の手順で作成したノイズ信号をフィルター処理したバージョンです。ノイズ信号を処理するフィルターを初期化します。
lp = dsp.FIRFilter('Numerator',fir1(31,0.5));% Low pass FIR filter
RLS フィルターのパラメーターを設定し、フィルターを初期化します。
M = 32; % Filter order delta = 0.1; % Initial input covariance estimate P0 = (1/delta)*eye(M,M); % Initial setting for the P matrix rlsfilt = dsp.RLSFilter(M,InitialInverseCovariance=P0);
RLS 適応フィルターを 1000 回反復して実行します。適応フィルターが収束すると、フィルター処理されたノイズが信号 + ノイズから完全に除去されます。誤差 e には元の信号のみが含まれます。
scope = timescope(TimeSpan=1000,YLimits=[-2,2], ... TimeSpanOverrunAction="scroll"); for k = 1:10 n = noiseSource(); % Noise s = signalSource(); d = lp(n) + s; [y,e] = rlsfilt(n,d); scope([s,e]); end release(scope);
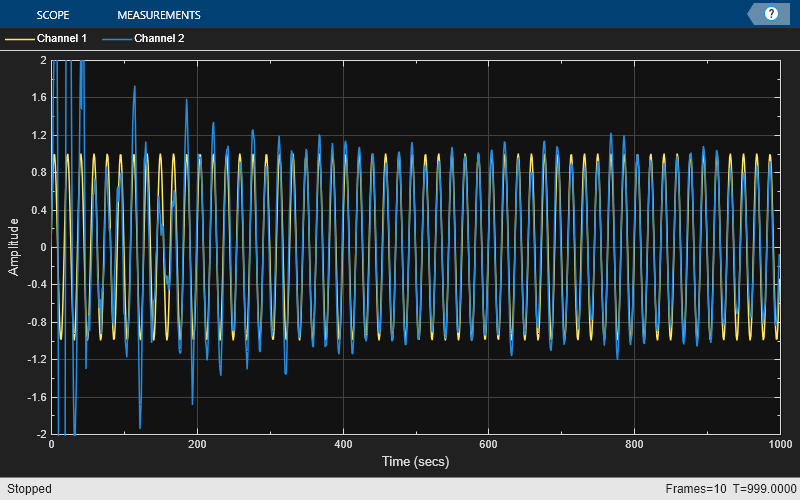
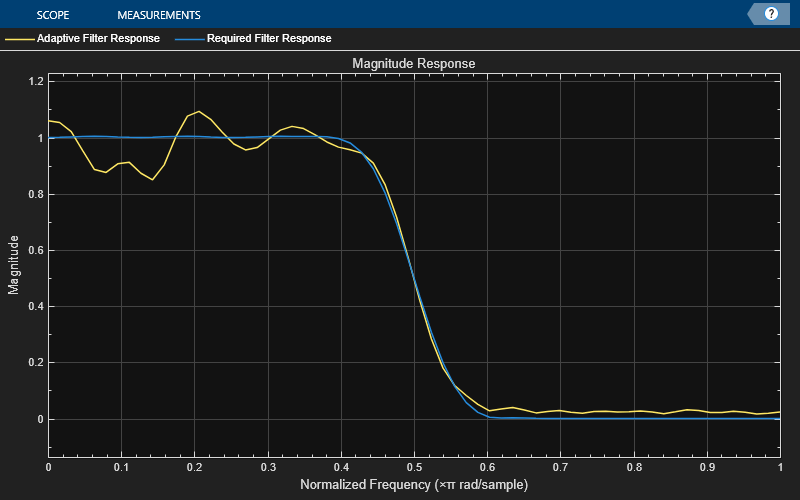
プロットは、FIR フィルターの応答に対する適応フィルター応答の収束を示します。
visualizer = dsp.DynamicFilterVisualizer(64,NormalizedFrequency=true,... MagnitudeDisplay="Magnitude", ... FilterNames=["Adaptive Filter Response","Required Filter Response"]); visualizer(rlsfilt.Coefficients,1,lp.Numerator,1);
参照
[1] S.Haykin, "Adaptive Filter Theory", 3rd Edition, Prentice Hall, N.J., 1996.