このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

適応フィルターとアプリケーションの概要

適応フィルターは、フィルターが最適な状態に収束するという目的で係数が変化するデジタル フィルターです。最適化基準はコスト関数であり、通常は適応フィルターの出力と目的の信号の間における誤差信号の平均二乗です。フィルターが係数を適応させると、平均二乗誤差 (MSE) が最小値に収束します。この状態では、フィルターが適応しており、係数が解に収束しています。そして、フィルターの出力 y(k) は目的の信号 d(k) に非常によく一致すると考えられます。入力データの特性 ("フィルター環境" とも呼ばれます) を変更すると、新しいデータに対して一連の新しい係数を生成することにより、フィルターは新しい環境に適応します。

一般的な適応フィルター アルゴリズム

DSP System Toolbox の適応フィルター

最小平均二乗 (LMS) ベースの FIR 適応フィルター

適応フィルター オブジェクト	適応アルゴリズム
dsp.BlockLMSFilter	ブロック LMS FIR 適応フィルター アルゴリズム
dsp.FilteredXLMSFilter	Filtered-X LMS FIR 適応フィルター アルゴリズム
dsp.LMSFilter	LMS FIR 適応フィルター アルゴリズム 正規化 LMS FIR 適応フィルター アルゴリズム 符号-データ LMS FIR 適応フィルター アルゴリズム 符号-誤差 LMS FIR 適応フィルター アルゴリズム 符号-符号 LMS FIR 適応フィルター アルゴリズム

適応フィルター ブロック	適応アルゴリズム
Block LMS Filter	ブロック LMS FIR 適応フィルター アルゴリズム
Fast Block LMS Filter	周波数領域におけるブロック LMS FIR 適応フィルター アルゴリズム
LMS Filter	LMS FIR 適応フィルター アルゴリズム 正規化 LMS FIR 適応フィルター アルゴリズム 符号-データ LMS FIR 適応フィルター アルゴリズム 符号-誤差 LMS FIR 適応フィルター アルゴリズム 符号-符号 LMS FIR 適応フィルター アルゴリズム
LMS Update	LMS FIR 重み更新アルゴリズム 正規化 LMS FIR 重み更新アルゴリズム 符号-データ LMS FIR 重み更新アルゴリズム 符号-誤差 LMS FIR 重み更新アルゴリズム 符号-符号 LMS FIR 重み更新アルゴリズム

再帰的最小二乗 (RLS) ベースの FIR 適応フィルター

適応フィルター オブジェクト	適応アルゴリズム
dsp.FastTransversalFilter	高速トランスバーサル最小二乗適応アルゴリズム スライディング ウィンドウ FTF 適応アルゴリズム
dsp.RLSFilter	QR 分解 RLS 適応アルゴリズム ハウスホルダー RLS 適応アルゴリズム ハウスホルダー SWRLS 適応アルゴリズム 再帰的最小二乗 (RLS) 適応アルゴリズム スライディング ウィンドウ (SW) RLS 適応アルゴリズム

適応フィルター ブロック	適応アルゴリズム
RLS Filter	指数加重再帰的最小二乗 (RLS) アルゴリズム

アフィン射影 (AP) FIR 適応フィルター

適応フィルター オブジェクト	適応アルゴリズム
dsp.AffineProjectionFilter	直接的な行列反転を使用するアフィン射影アルゴリズム 再帰的な行列更新を使用するアフィン射影アルゴリズム ブロック アフィン射影適応アルゴリズム

周波数領域 (FD) における FIR 適応フィルター

適応フィルター オブジェクト	適応アルゴリズム
dsp.FrequencyDomainAdaptiveFilter	制約付き周波数領域適応アルゴリズム 制約なし周波数領域適応アルゴリズム 分割された制約付き周波数領域適応アルゴリズム 分割された制約なし周波数領域適応アルゴリズム

適応フィルター ブロック	適応アルゴリズム
Frequency-Domain Adaptive Filter	制約付き周波数領域適応アルゴリズム 制約なし周波数領域適応アルゴリズム 分割された制約付き周波数領域適応アルゴリズム 分割された制約なし周波数領域適応アルゴリズム

ラティス ベース (L) FIR 適応フィルター

適応フィルター オブジェクト	適応アルゴリズム
dsp.AdaptiveLatticeFilter	勾配適応ラティス フィルター適応アルゴリズム 最小二乗ラティス適応アルゴリズム QR 分解 RLS 適応アルゴリズム

これらのアルゴリズムの詳細については、それぞれのリファレンス ページのアルゴリズムに関する節を参照してください。理論の詳細については、適応フィルターの参考文献 [1] および [2] を参照してください。

適応フィルターの選択

フィルターが適応したときの定常状態では、フィルターの出力と目的の信号の間で誤差が最小になります (ゼロではありません)。この誤差は、定常偏差と呼ばれます。フィルターが最適な状態に収束する速度 (収束速度) は、入力信号の性質、適応フィルター アルゴリズムの選択、アルゴリズムのステップ サイズなど、複数の要因の影響を受けます。通常、フィルター アルゴリズムの選択は、アプリケーションに必要な収束性能、アルゴリズムの計算量、環境におけるフィルターの安定性、その他の制約などの要因に依存します。

LMS アルゴリズムは、実装がシンプルですが、安定性の問題があります。正規化されたバージョンの LMS アルゴリズムは、収束速度と安定性が改善されますが、計算量が増加します。この 2 つを比較する例については、LMS アルゴリズムと正規化 LMS アルゴリズムの収束性能の比較を参照してください。RLS アルゴリズムは、非常に安定しており、時間依存性がある環境で非常に良好に機能しますが、LMS アルゴリズムより計算量が増加します。比較については、RLS 適応フィルター アルゴリズムと LMS 適応フィルター アルゴリズムの比較を参照してください。アフィン射影フィルターは、入力が色付きである場合に良好に機能し、収束性能が非常に優れています。適応ラティス フィルターは、収束が優れていますが、計算コストが増加します。アルゴリズムの選択は、アプリケーションの仕様と環境に依存します。

平均二乗誤差の性能

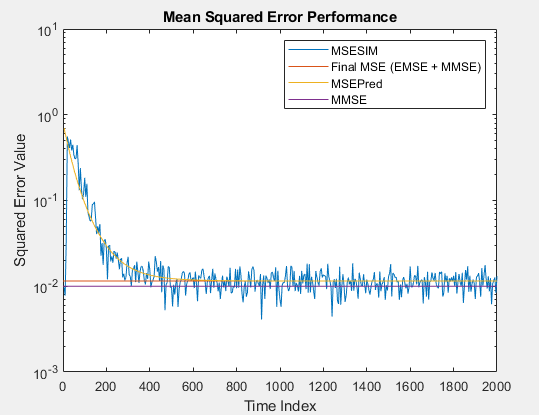
適応フィルターの出力と目的の信号の間で誤差信号の平均二乗を最小化することが、最も一般的な適応フィルターの最適化基準です。実装している適応フィルターの実際の MSE (MSESIM) は、関数 msesim を使用して判別できます。MSE の軌跡は、関数 msepred を使用して計算される予測 MSE (MSEPred) の軌跡に従うと予想されます。最小平均二乗誤差 (MMSE) は、ウィーナー フィルターを使用して関数 msepred によって推定されます。ウィーナー フィルターは、ウィーナー フィルターによってフィルター処理された入力信号と目的の信号の間で平均二乗誤差を最小化します。大きい値の平均二乗誤差は、適応フィルターが目的の信号を正確には追跡できないことを示します。平均二乗誤差が最小値である場合、適応フィルターは最適です。関数 msepred によって決定される過剰平均二乗誤差 (EMSE) は、適応フィルターによって導入される MSE と対応するウィーナー フィルターによって生成される MMSE の差です。以下に示す最終的な MSE は、EMSE と MMSE の和であり、収束後の予測 MSE と等しくなります。

一般的な使用例

システム同定 –– 適応フィルターの使用による未知のシステムの同定

一般的な適応フィルター アプリケーションの 1 つは、適応フィルターを使用して不明な通信チャネルの応答や大会議室の周波数応答といった未知のシステムを同定し、相当数の種々に異なるアプリケーションを選択します。その他のアプリケーションには、エコー キャンセルやチャネルの識別などがあります。

次の図では、未知のシステムが適応フィルターと並列に配置されています。このレイアウトが表しているのは、可能性のある多数の構造の 1 つにすぎません。影付き領域には適応フィルター システムが含まれています。

明らかに、e(k) が非常に小さい場合、適応フィルター応答は未知のシステムの応答に近くなります。この場合、適応フィルターと未知のシステムの両方に同じ入力が与えられます。たとえば、未知のシステムがモデムの場合、入力はホワイト ノイズを表すことがよくあります。これは、インターネット サービス プロバイダーにログインするとモデムから聞こえる音声の一部です。

逆システム同定 –– 未知のシステムに対する逆応答の決定

未知のシステムを適応フィルターと直列に配置することで、e(k) が非常に小さくなるとフィルターは未知のシステムの逆になるように適応します。図に示すように、このプロセスでは、加算時にデータを同期させるため、目的の信号 d(k) のパスに遅延を挿入する必要があります。遅延を追加することでシステムの因果性が維持されます。

遅延を含めて未知のシステムにより生じる遅延を考慮することで、この条件が回避されます。

Plain Old Telephone Systems (POTS) は一般に逆システム同定を使用して銅の伝達媒体を補正します。データまたは音声を電話回線で送信する場合、銅線は、高周波数 (またはデータ転送速度) でロールオフする応答と、他の異常も含んでいるフィルターのように機能します。

有線応答の逆である応答をもつ適応フィルターを追加し、リアルタイムで適応するようにフィルターを設定して、フィルターでロールオフと異常を補正させ、電話システムで使用可能な周波数出力範囲とデータ転送速度を増大させます。

ノイズまたは干渉の除去 –– 適応フィルターを使用した、未知のシステムからのノイズの除去

ノイズ キャンセリングでは、適応フィルターにより信号からリアルタイムでノイズを除去できます。ここでは、クリーンアップするための目的の信号は、ノイズと目的の情報を結合します。ノイズを除去するには、目的の信号から除去するノイズに相関している適応フィルターに信号 n'(k) を送ります。

フィルターへの入力ノイズが目的の信号を付随する不要なノイズに相関している限り、適応フィルターはその係数を調整して y(k) と d(k) 間の差の値を減らし、ノイズを除去して e(k) にクリーンな信号を出力します。このアプリケーションでは、誤差信号はゼロに収束するのではなく、実際に入力データ信号に収束することに注目してください。

予測 –– 周期信号の将来の値の予測

信号を予測するには、いくつかの重要な仮定を行わなければなりません。信号が定常であるか、時間の経過に沿って緩やかに変化するかのいずれかで、時間に伴い周期的でもあると仮定します。

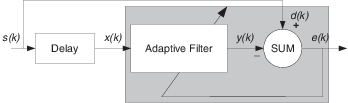
これらの仮定を受け入れる場合、適応フィルターで、過去の値に基づき目的の信号の将来値を予測しなければなりません。s(k) が周期的で、フィルターが前の値を記憶するのに十分な長さである場合、入力信号に遅延をもつこの構造は予測を実行できます。この構造を使用して、確率的ノイズ信号から周期信号を除去する場合もあります。

最後に、ほとんどの対象システムに、4 つの適応フィルター構造のうち 1 つ以上の要素が含まれていることに注目してください。実際の構造を慎重に確認するために、適応フィルターの適応対象を特定しなければならない場合があります。

また、この図でわかりやすくするために、アナログ デジタル (A/D) コンポーネントとデジタル アナログ (D/A) コンポーネントは表示されません。適応フィルターは本質的にデジタルであると仮定されており、多くの問題によってアナログ データが生成されるため、アナログ領域に対する入力信号の変換がおそらく必要になります。

参照

[1] Hayes, Monson H., Statistical Digital Signal Processing and Modeling. Hoboken, NJ: John Wiley & Sons, 1996, pp.493–552.

[2] Haykin, Simon, Adaptive Filter Theory. Upper Saddle River, NJ: Prentice-Hall, Inc., 1996.