周波数変調

周波数変調 (FM) は、メッセージにより定振幅信号の周波数を変調するベースバンド変調方式です。送信信号は、データ遷移時に搬送波周波数を切り替えることによって作成されます。変調信号は周波数の違いにより、受信機でコヒーレントに分離 (復調) できます。FM は、位相変調の特殊なケースと見なすことができます。

Communications Toolbox™ ソフトウェアには、以下の変調関数と復調関数、System object、および周波数偏移変調 (FSK) 変調をモデル化するためのブロックが含まれています。

関数	System object	ブロック
`fskmod`, `fskdemod`	`comm.FSKModulator`, `comm.FSKDemodulator`	M-FSK Modulator Baseband, M-FSK Demodulator Baseband

FSK

FSK は、周波数が異なる直交信号の特殊なケースです。

Proakis ([2]) で説明されているように、信号波形は次のように表すことができます。

$s_{m} = \sqrt{\frac{2 ε}{T}} \cos (2 π f_{c} t + 2 π m Δ f t), \begin{matrix} \end{matrix} 1 \leq m \leq M, \begin{matrix} \end{matrix} 0 \leq t \leq T$

周波数変調の例

以下の例では、FM 変調方式を示します。

FSK 信号スペクトルのプロット

ライブスクリプトを開く

FSK 変調信号を生成し、スペクトル特性を表示します。

関数のパラメーターを設定します。

M = 4;       % Modulation order
freqsep = 8; % Frequency separation (Hz)
nsamp = 8;   % Number of samples per symbol
Fs = 32;     % Sample rate (Hz)

ランダム M-ary シンボルを生成します。

x = randi([0 M-1],1000,1);

FSK 変調を適用します。

y = fskmod(x,M,freqsep,nsamp,Fs);

スペクトルアナライザー System object™ を作成し、これを呼び出して信号スペクトルのプロットを表示します。

specAnal = spectrumAnalyzer(SampleRate=Fs);
specAnal(y)

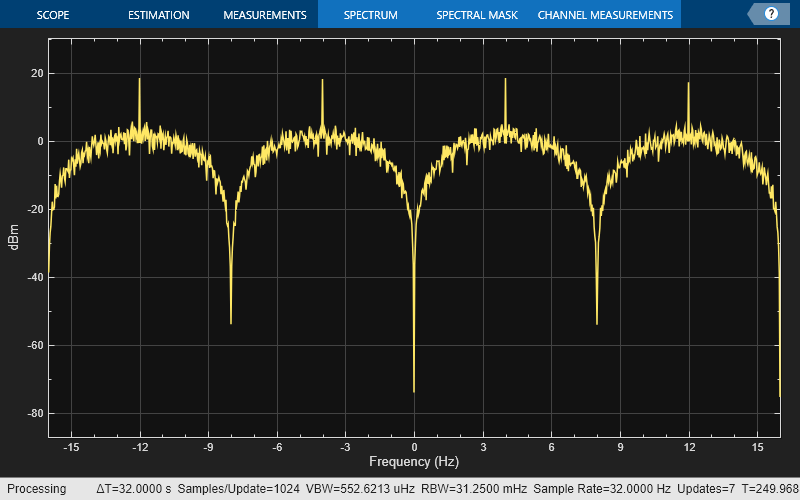
さまざまなフェージングチャネルでの FSK 変調の適用

ライブスクリプトを開く

FSK 信号をレイリーマルチパスフェージングチャネル経由で渡します。信号帯域幅を変更して、フェージングチャネルの影響を FSK スペクトルで観察します。

フラットフェージングチャネル

変調次数を 4、変調後のシンボルレートを 45 bps、周波数分離を 200 Hz に、それぞれ設定します。

M = 4;           % Modulation order
symbolRate = 45; % Symbol rate (bps)
freqSep = 200;   % Frequency separation (Hz)

シンボルあたりのサンプル数パラメーター sampPerSym を、変調次数、周波数分離およびシンボルレートの関数として計算します。出力信号のエイリアシングを回避するには、sampPerSym と symbolRate の積が M と freqSep の積より大きくなければなりません。FSK 出力信号のサンプルレートを計算します。

sampPerSym = ceil(M*freqSep/symbolRate);
fsamp = sampPerSym*symbolRate;

FSK 変調器を作成します。

fskMod = comm.FSKModulator(M, ...
    FrequencySeparation=freqSep, ...
    SamplesPerSymbol=sampPerSym, ...
    SymbolRate=symbolRate);

3 パスフェージングチャネルのパス遅延と平均パスゲインを設定します。

pathDelays = [0 3 10]*1e-6; % Discrete delays (s)
avgPathGains = [0 -3 -6];   % Average path gains (dB)

慣例により、最初のパスの遅延は一般にゼロに設定されます。それ以降のパスの場合、1 マイクロ秒の遅延はパス長では 300 m の違いに相当します。チャネルの平均遅延プロファイルは、パス遅延とパスゲインの影響を受けます。

定義されたパラメーターを使用してレイリーチャネルを作成します。Visualization プロパティを設定して、インパルス応答と周波数応答を表示します。

channel = comm.RayleighChannel( ...
    SampleRate=fsamp, ...
    PathDelays=pathDelays, ...
    AveragePathGains=avgPathGains, ...
    MaximumDopplerShift=0.01, ...
    Visualization='Impulse and frequency responses', ...
    SamplesToDisplay='10%');

ランダムデータシンボルを生成して FSK 変調を適用します。

data = randi([0 3],2000,1);
modSig = fskMod(data);

FSK 変調信号とフラットフェージングチャネルフィルター処理後の受信信号をプロットするスペクトルアナライザーオブジェクトを作成します。

sa1 = spectrumAnalyzer( ...
    SampleRate=fsamp, ...
    ChannelNames=["FSK modulated signal", ...
        "Flat fading channel"]);

変調信号は、200 Hz で区切られ、それぞれが約 20 dBm のピーク強度をもつ 4 つのトーンで構成されています。

信号をレイリーフェージングチャネルを通して渡し、25 dB の S/N 比をもつ AWGN を適用します。

snrdB = 25;
raylFadedData = channel(modSig);

rxSig = awgn(raylFadedData,snrdB);

インパルス応答と周波数応答から、チャネルがフラットであるかのように動作していることが分かります。このようにフラットな応答になるのは、信号帯域幅 800 Hz がコヒーレンス帯域幅 50 kHz よりもはるかに小さいためです。

チャネルフィルター処理の前と後で、FSK 変調信号の信号スペクトルをプロットします。FSK 信号で構成される 4 つのトーンは、同一の周波数分離とピーク強度レベルを互いに相対するように維持します。絶対ピーク強度レベルは、フェージングチャネルによって低下しています。

sa1(modSig,rxSig)
release(sa1)

周波数選択性フェージング

シンボルレートを 45 kbps、周波数分離を 200 kHz に上げます。シンボルあたりのサンプル数とサンプルレートパラメーターの新しい値を計算します。FSK 変調器オブジェクトを解放し、その構成を更新します。

symbolRate = 45e3;
freqSep = 200e3;

release(fskMod)
fskMod.SymbolRate = symbolRate;
fskMod.FrequencySeparation = freqSep;

FSK 変調信号と周波数選択性フェージングチャネルフィルター処理後の受信信号をプロットするスペクトルアナライザーオブジェクトを作成します。

sampPerSym = ceil(M*freqSep/symbolRate);
sa2 = spectrumAnalyzer( ...
    SampleRate=sampPerSym*symbolRate, ...
    ChannelNames=["FSK modulated signal", ...
        "Frequecy-selective fading channel"]);

送信データに FSK 変調を適用します。

modSig = fskMod(data);

チャネルオブジェクトを解放し、チャネルのサンプルレートプロパティを更新します。レイリーフェージングチャネルを通して信号を渡し、AWGN を適用します。インパルス応答と周波数応答から、マルチパスフェージングが周波数選択的であることが分かります。

release(channel)
fsamp = sampPerSym*symbolRate;
channel.SampleRate = fsamp;

rxSig = awgn(channel(modSig),25);

チャネルフィルター処理の前と後で、FSK 変調信号の信号スペクトルをプロットします。スペクトルの形状はフラットフェージングの場合と同じですが、今度は 4 つのトーンが 200 kHz で区切られています。4 つのトーンはまだ識別可能ですが、周波数選択性フェージングによって、トーンの相対的なピーク強度レベルが異なっています。800 kHz の信号帯域幅が、50 kHz のコヒーレンス帯域幅よりも大きくなっています。

sa2(modSig,rxSig)
release(sa2)

参照

[1] Sklar, Bernard. Digital Communications: Fundamentals and Applications. 2nd ed. Upper Saddle River, N.J: Prentice-Hall PTR, 2001.

[2] Proakis, John G. Digital Communications. 5th ed. New York: McGraw Hill, 2007.

参考

周波数変調

FSK

周波数変調の例

FSK 信号スペクトルのプロット

さまざまなフェージング チャネルでの FSK 変調の適用

参照

参考

関数

オブジェクト

ブロック

関連するトピック

さまざまなフェージングチャネルでの FSK 変調の適用