Simulink での OSTBC と TCM の連結

この例では次を使用します。

このモデルでは、送信アンテナ 2 つ、受信アンテナ 1 つをもつ多入力多出力 (MIMO) チャネルで情報を伝送するためにトレリス符号化変調 (TCM) と連結された直交空間時間ブロック符号 (OSTBC) について示します。

はじめに

OSTBC [ 1 ]、[ 2 ] は MIMO 無線通信において効果的な手法です。この手法は完全な空間ダイバーシティ数を利用して、シンボル単位で最尤 (ML) 復号化を行います。ただし、符号化ゲインは得られません。受信機の OSTBC のコンバイナーは送信されたシンボルの軟情報を提供し、この情報は外符号の復号化や復調に利用することができます。

TCM [ 3 ] は、符号化と変調を統合して大規模な符号化ゲインを得られるようにするための帯域幅効率化方式です。TCM を内符号と連結すると、通常はパフォーマンスが向上します。

この例では、OSTBC と TCM の連結方式の利点、つまり OSTBC によって得られる空間ダイバーシティゲインと TCM によって得られる符号化ゲインについて説明します。比較のため、TCM と OSTBC の一方だけを組み込んだ 2 つの基準モデルも示します。基準モデルと比較したときの連結方式のダイバーシティゲインと符号化ゲインの優位性は、シミュレーションの結果から明白です。OSTBC と TCM の連結に関する詳細については、[4] や [5] などの参考文献を参照してください。

例の構造

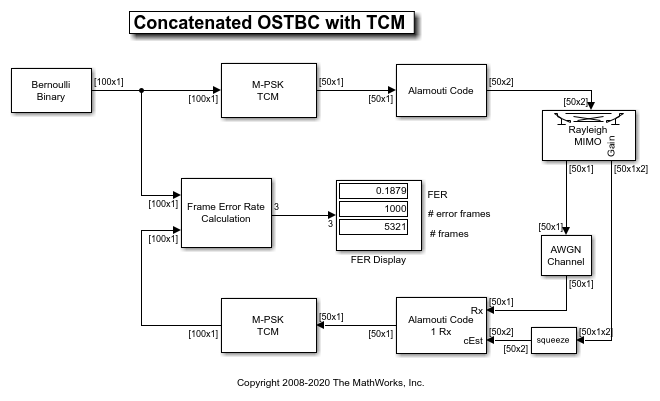
モデルによって実行される個々のタスクには、以下が含まれます。

ランダムデータの生成

Bernoulli Binary Generatorブロックは、このシミュレーション用の情報源を作成します。このブロックは 100 のランダムなビットのフレームを生成します。Samples per frame パラメーターは、出力フレームの長さを決定します (この場合は 100)。

トレリス符号化変調 (TCM)

M-PSK TCM Encoderブロックは、メッセージデータを Bernoulli Binary Generator から単位平均エネルギーをもつ PSK コンスタレーションへ変調します。Trellis structure パラメーターは、TCM のトレリスを指定するため、任意の MATLAB® 構造体を受け取ります。M-ary number パラメーターは、PSK コンスタレーションのサイズを指定します。この例では、トレリス状態が 8 つある 8-PSK コンスタレーションに Ungerboeck TCM 方式を使用します [ 3 ]。それに応じて、Trellis structure パラメーターを poly2trellis([2 3], [1 2 0; 4 1 2]) に設定します。このブロックの出力フレーム長は 50 であり、2 つの入力ビットそれぞれが 1 つのシンボルを生成します。

M-PSK TCM Decoderブロックは、TCM 用 Viterbi アルゴリズムを使用して、OSTBC コンバイナーからの信号を復号化します。Operation mode パラメーターを Truncated に設定して各フレームを個別に処理します。Traceback depth パラメーターを 30 に設定します。これは、TCM の拘束長と比較した場合、損失がほとんどない性能を確保するには十分の長さです。

直交空間時間ブロック符号 (OSTBC)

OSTBC Encoderブロックは、2 つの送信アンテナ用の Alamouti コード [1] を使用して、TCM 符号化器からの情報シンボルを符号化します。このブロックの出力は 50x2 行列で、各列のエントリは 1 つのアンテナから送信されたデータに対応します。

OSTBC Combinerブロックは、受信アンテナからの受信信号をチャネル状態情報 (CSI) と組み合わせて送信シンボルの推定値を出力します。この推定値は、M-PSK TCM 復号化器にフィードされます。この例では、CSI は受信機側で完全に既知であると仮定します。

2x1 MIMO チャネル

MIMO Fading Channel ブロックは、2x1 周波数フラットレイリーフェージングチャネルをシミュレートします。Sample rate (Hz) パラメーターは、入力信号長とモデルサンプル時間に基づいて計算され、500000 に設定されます。Maximum Doppler shift (Hz) パラメーターは 30 に設定されます。この値を使用すると、MIMO チャネルが準静的なフェージングチャネルのように動作します。つまり、1 つのフレームの送信中は一定で、複数のフレームの場合は変化します。

受信機のノイズ

AWGN Channelブロックは、受信機にホワイトガウスノイズを加えます。TCM 用の PSK コンスタレーションに単位平均エネルギーがあり、MIMO チャネルのパスゲインが正規化されるので、Mode パラメーターは Signal to noise ratio (SNR) モードに設定し、Input signal power, referenced to 1 ohm (watts) パラメーターを 2 に設定します。

フレームエラーレート (FER) の計算

Frame Error Rate (FER) Calculation サブシステムは復号化されたビットをフレームごとに元のソースビットと比較し、エラーを検出し、シミュレーション中に FER を動的に更新します。このサブシステムの出力は、FER、観測された誤りのあるフレーム数、および処理したフレーム数を含む 3 要素ベクトルです。このベクトルはError Rate Calculationブロックから生成され、また複数の SNR 値用のシミュレーションを容易にするために MATLAB® ワークスペース変数 FER_Data として保存されます (下記参照)。

Stop simulation パラメーターがチェックされ、シミュレーションの期間を制御します。シミュレーションは、誤りのあるフレーム数の目標数 (Target number of errors パラメーターで指定)、または全フレーム数の最大数 (Maximum number of symbols パラメーターで指定) のどちらかを検出すると停止します。

次に、比較に使用した 2 つの参照モデルについて簡単に説明します。

フラットレイリーフェージングチャネルを介した TCM

モデル commtcm.slx は、単入力単出力 (SISO) のフラットレイリーフェージングチャネルを介した上記の連結方式での TCM をシミュレートします。空間時間符号化は使用しません。SISO Fading Channel ブロックの仕様は、上記モデルの 2x1 MIMO チャネルの 1 つのサブチャネルと同じです。シンボル期間ごとに 1 つのシンボルしか転送されないので、AWGN Channelブロックの Input signal power, referenced to 1 ohm (watts) パラメーターを 1 に設定します。

チャネルイコライザー

チャネルイコライザーサブシステムは、受信機のフェージングチャネル効果を補正します。その出力は、復号化を行うために M-PSK TCM Decoder ブロックにフィードされます。このモデルでは、チャネルはフラットレイリーフェージングです。

2x1 フラットレイリーフェージングチャネルを介した OSTBC

モデル commostbc.slx は、上記の連結方式での TCM を QPSK 変調に置き換えて、両方のモデルのシンボル (フレーム) レートが同じになるようにします。また、TCM-OSTBC 連結モデルと同じ 2x1 MIMO Fading Channel ブロックを使用します。QPSK Modulator Basebandブロックは、情報ビットを QPSK コンスタレーションにマッピングします。QPSK Demodulator Basebandブロックは、OSTBC コンバイナーからの信号を復調します。

性能

FER 対 SNR の動作特性曲線を作成するには、複数の SNR 値によるシミュレーションが複数回必要です。これは、sim コマンドを使用して実行できます。最初に、シミュレーションパラメーターをいくつか定義し、

      SNRRange = 10:2:24;
      maxNumErrs = 1e3;  % Number of frame errors
      maxNumFrms = 5e6;  % Number of frames processed

次に、動作特性を可視化するために Figure を初期化します。

      fig = figure;
      grid on;
      hold on;
      ax = fig.CurrentAxes;
      ax.YScale = 'log';
      xlim([SNRRange(1), SNRRange(end)]);
      ylim([1e-4 1]);

      xlabel('SNR (dB)');
      ylabel('FER');
      fig.NumberTitle = 'off';
      fig.Rrenderer = 'zbuffer';
      fig.Name = 'Concatenated OSTBC with TCM';
      title('Concatenated OSTBC with TCM');

OSTBC-TCM 連結モデルをシミュレートするために、次のコマンドを実行して、シミュレーションを複数回実行し、結果をプロットします。

      FERTCMOSTBC = zeros(length(SNRRange), 3);
      for idx = 1:length(SNRRange)
          SNR = SNRRange(idx);
          sim('commtcmostbc');
          FERTCMOSTBC(idx, :) = FER_Data;
          h1 = semilogy(SNRRange(1:idx), FERTCMOSTBC(1:idx, 1), 'r+');
      end
      fitFERTCMOSTBC = berfit(SNRRange, FERTCMOSTBC(:, 1)');
      semilogy(SNRRange, fitFERTCMOSTBC, 'r');

同様に、次のコマンドを実行して 2 つの参照モデルをシミュレートします。

      FERTCM = zeros(length(SNRRange), 3);
      for idx = 1:length(SNRRange)
          SNR = SNRRange(idx);
          sim('commtcm');
          FERTCM(idx, :) = FER_Data;
          h2 = semilogy(SNRRange(1:idx), FERTCM(1:idx, 1), 'gp');
      end
      fitFERTCM = berfit(SNRRange, FERTCM(:, 1)');
      semilogy(SNRRange, fitFERTCM, 'g');

      FEROSTBC = zeros(length(SNRRange), 3);
      for idx = 1:length(SNRRange)
          SNR = SNRRange(idx);
          sim('commostbc');
          FEROSTBC(idx, :) = FER_Data;
          h3 = semilogy(SNRRange(1:idx), FEROSTBC(1:idx, 1), 'bo');
      end
      fitFEROSTBC = berfit(SNRRange, FEROSTBC(:, 1)');
      semilogy(SNRRange, fitFEROSTBC, 'b');

      legend([h1, h2, h3], 'TCM + OSTBC', 'TCM', 'OSTBC');

SNR に対する FER の動作特性の結果が次の図のように表示されます。

予期されたとおり、この連結方式で TCM 方式より大幅に優れたダイバーシティゲイン、および Alamouti コードより約 2 dB 上回る符号化ゲインが得られることが実証されました。

その他の調査

シミュレーションモデルを読み込むとき、MATLAB® ワークスペースに変数が作成されます。これらの変数を変更して、システムパフォーマンスにおける Samples per frame (変数 frameLen)、Trellis structure (変数 trellis) または Maximum Doppler shift (Hz) (変数 maxDopp) などのさまざまなパラメーター設定の効果を確認できます。

参考文献

S. M. Alamouti, "A simple transmit diversity technique for wireless communications," IEEE® Journal on Selected Areas in Communications, vol. 16, no. 8, pp. 1451-1458, Oct. 1998.
V. Tarokh, H. Jafarkhami, and A. R. Calderbank, "Space-time block codes from orthogonal designs," IEEE Transactions on Information Theory, vol. 45, no. 5, pp. 1456-1467, Jul. 1999.
G. Ungerboeck, "Channel coding with multilevel/phase signals," IEEE Transactions on Information Theory, vol. IT-28, no. 1, pp. 55-67, Jan. 1982.
S. M. Alamouti, V. Tarokh, and P. Poon, "Trellis-coded modulation and transmit diversity: Design criteria and performance evaluation," in Proc. IEEE International Conference on Universal Personal Communications (ICUPC'98), Florence, Italy, Oct. 1998, pp. 703-707.
Y. Gong and K. B. Letaief, "Concatenated space-time block coding with trellis coded modulation in fading channels," IEEE Transactions on Wireless Communications, vol. 1, no. 4, pp. 580-590, Oct. 2002.