comm.GMSKModulator

GMSK 法を使用した変調

このページをすべて展開する

説明

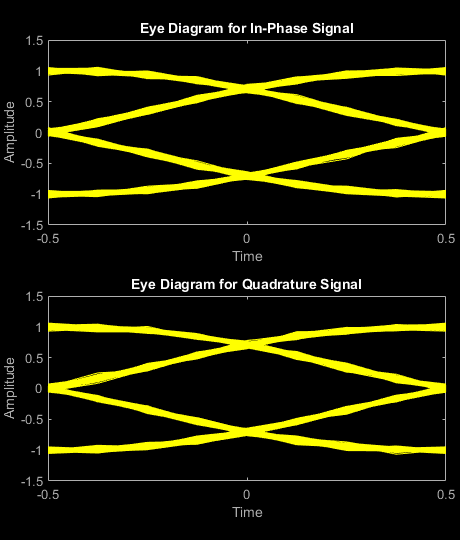
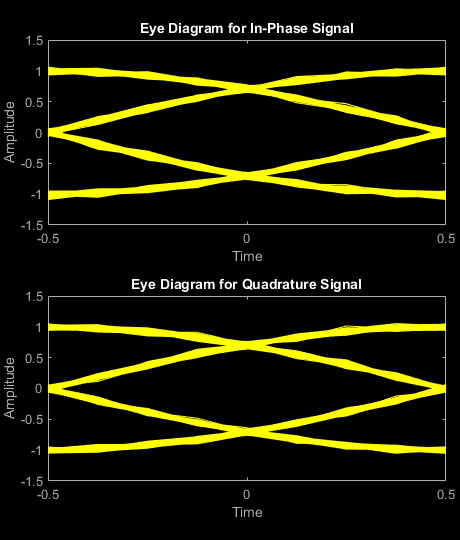
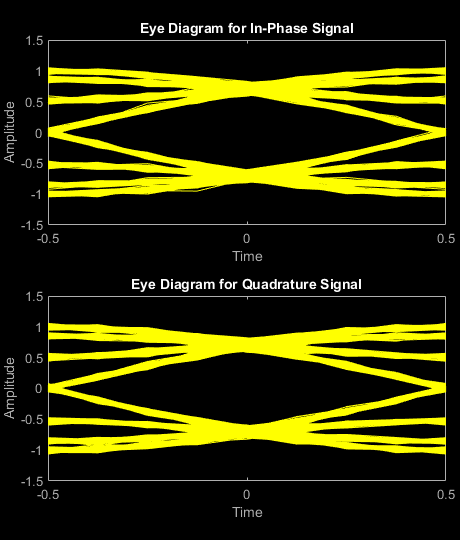
comm.GMSKModulatorSystem object™ は、ガウス最小偏移変調 (GMSK) 法を使用して変調します。出力は、変調信号のベースバンド表現です。詳細については、アルゴリズムを参照してください。

GMSK 法を使用して信号を変調するには、次のようにします。

comm.GMSKModulator オブジェクトを作成し、そのプロパティを設定します。
関数と同様に、引数を指定してオブジェクトを呼び出します。

System object の機能の詳細については、System object とはを参照してください。

作成

構文

gmskmodulator = comm.GMSKModulator

gmskmodulator = comm.GMSKModulator(Name,Value)

説明

例

gmskmodulator = comm.GMSKModulator は、GMSK 変調方式を使用して入力信号を変調する変調器 System object を作成します。

例

gmskmodulator = comm.GMSKModulator(Name,Value) は、名前と値からなる 1 つ以上の引数を使用してプロパティを設定します。たとえば、comm.GMSKModulator(PulseLength=6) はガウスパルス整形の長さを 6 つのシンボル区間として指定します。

プロパティ

すべて展開する

特に指定がない限り、プロパティは "調整不可能" です。つまり、オブジェクトの呼び出し後に値を変更することはできません。オブジェクトは呼び出すとロックされ、ロックを解除するには関数 release を使用します。

プロパティが "調整可能" の場合、その値をいつでも変更できます。

プロパティ値の変更の詳細については、System object を使用した MATLAB でのシステム設計を参照してください。

`BitInput` — 入力をビットとして提供するオプション
`false` または `0` (既定値) | `true` または `1`

入力をビットとして提供するオプション。数値または logical の 0 (false) または 1 (true) として指定します。

このプロパティを false に設定した場合、入力 X は -1 または 1 の値をもつ列ベクトルでなければなりません。
このプロパティを true に設定した場合、入力 X は 0 と 1 の列ベクトルでなければなりません。

データ型: logical

`BandwidthTimeProduct` — 帯域幅とシンボル時間の積
`0.3` (既定値) | 正のスカラー

ガウスパルス整形の帯域幅とシンボル時間の積。正のスカラー値として指定します。詳細については、アルゴリズムを参照してください。

変調される信号に対するこのプロパティの効果を確認するには、GMSK 変調される信号に対する帯域幅と時間の積による効果の例を参照してください。

データ型: double

`PulseLength` — パルス長
`4` (既定値) | 正の整数

パルス長。正の整数として指定します。パルス長の値は、シンボル区間でのガウスパルス整形の長さを表します。

データ型: double

`SymbolPrehistory` — シンボルプレヒストリ
`1` (既定値) | `-1` | ベクトル

シンボルプレヒストリ。-1、1、またはこれらの値と等しい要素を持つベクトルとして指定します。このプロパティは、オブジェクトの最初の呼び出しの前に、変調器によって使用されるデータシンボルを新しいものから順番に定義します。

スカラー値は長さ PulseLength – 1 のベクトルに展開されます。
ベクトルの場合、長さが PulseLength – 1 でなければなりません。

データ型: double

`InitialPhaseOffset` — 初期位相オフセット
`0` (既定値) | 数値スカラー

変調波形の初期位相オフセット (ラジアン単位)。数値スカラーとして指定します。

データ型: double

`SamplesPerSymbol` — 出力シンボルあたりのサンプル数
`8` (既定値) | 正の整数

シンボルあたりのサンプル数。正の整数として指定します。シンボルあたりのサンプル数は、入力サンプルから出力サンプルへのアップサンプリング係数を表します。

データ型: double

`OutputDataType` — 出力のデータ型
`'double'` (既定値) | `'single'`

出力のデータ型。'double' または 'single' として指定します。

使用法

構文

Y = gmskmodulator(X)

説明

Y = gmskmodulator(X) は GMSK 変調を入力データに適用し、変調された GMSK ベースバンド信号を返します。

入力引数

すべて展開する

`X` — 入力データ
整数 | 列ベクトル

入力データ。整数、あるいは整数またはビットからなる列ベクトルとして指定します。

BitInput を false に設定する場合、入力データは倍精度または符号付き整数でなければなりません。
BitInput を true に設定する場合、入力データは倍精度または logical でなければなりません。

このオブジェクトは可変サイズの入力を受け入れます。オブジェクトがロックされると、各入力チャネルのサイズは変更できますが、チャネルの数は変更できません。詳細については、Variable-Size Signal Support with System Objectsを参照してください。

データ型: double | int8 | int16 | int32 | logical

出力引数

すべて展開する

`Y` — GMSK 変調されたベースバンド信号
ベクトル

GMSK 変調されたベースバンド信号。列ベクトルとして返されます。

出力ベクトル Y の長さは、SamplesPerSymbol プロパティ値で指定したシンボルあたりのサンプル数に入力サンプル数を掛け合わせたものと同じです。OutputDataType プロパティは、出力のデータ型を指定します。

データ型: double | single

オブジェクト関数

オブジェクト関数を使用するには、System object を最初の入力引数として指定します。たとえば、obj という名前の System object のシステムリソースを解放するには、次の構文を使用します。

release(obj)

すべて展開する

すべての System object に共通

`step`	System object のアルゴリズムの実行
`release`	リソースを解放し、System object のプロパティ値と入力特性の変更を可能にします。
`reset`	System object の内部状態のリセット

例

すべて折りたたむ

バイナリデータの GMSK 信号へのマッピング

ライブスクリプトを開く

0 と 1 のバイナリシーケンスを GMSK 変調器の出力にマッピングします。このマッピングは MSK 変調にも適用されます。

バイナリ入力を受け入れる GMSK 変調器を作成します。この変調器のパルス長とシンボルあたりのサンプル数の値は 1 に設定します。

gmskmodulator = comm.GMSKModulator( ...
    BitInput=true, ...
    PulseLength=1, ...
    SamplesPerSymbol=1);

すべて 0 の入力シーケンスを作成します。シーケンスを変調します。

x = zeros(5,1);
y = gmskmodulator(x)

y = 5×1 complex

   1.0000 + 0.0000i
   0.0000 - 1.0000i
  -1.0000 - 0.0000i
  -0.0000 + 1.0000i
   1.0000 + 0.0000i

各点の位相角を決定します。関数 unwrap を使用してトレンドを表示します。

theta = unwrap(angle(y))

theta = 5×1

         0
   -1.5708
   -3.1416
   -4.7124
   -6.2832

0 のシーケンスにより、サンプル間で位相が -π/2 シフトします。

変調器をリセットします。すべて 1 の入力シーケンスを変調します。

reset(gmskmodulator)
x = ones(5,1);
y = gmskmodulator(x)

y = 5×1 complex

   1.0000 + 0.0000i
   0.0000 + 1.0000i
  -1.0000 + 0.0000i
  -0.0000 - 1.0000i
   1.0000 - 0.0000i

各点の位相角を決定します。関数 unwrap を使用してトレンドを表示します。

theta = unwrap(angle(y))

theta = 5×1

         0
    1.5708
    3.1416
    4.7124
    6.2832

1 のシーケンスにより、サンプル間で位相が +π/2 シフトします。

AWGN 環境下の GMSK 信号

ライブスクリプトを開く

GMSK 変調器と復調器のペアを作成します。AWGN チャネルオブジェクトを作成します。

gmskmodulator = comm.GMSKModulator( ...
    BitInput=true, ...
    InitialPhaseOffset=pi/4);
gmskdemodulator = comm.GMSKDemodulator( ...
    BitOutput=true, ...
    InitialPhaseOffset=pi/4);
channel = comm.AWGNChannel( ...
    NoiseMethod='Signal to noise ratio (SNR)', ...
    SNR=0);

エラーレート計算機を作成し、ビタビアルゴリズムによって発生する変調器と復調器の間の遅延を考慮します。

errorRate = comm.ErrorRate( ...
    ReceiveDelay=gmskdemodulator.TracebackDepth);

以下の手順を繰り返して 100 フレームのデータを処理します。

300 要素のランダムなバイナリデータのベクトルを生成します。
データを GMSK 変調します。
変調データを AWGN チャネルを介して渡します。
データを GMSK 復調します。
データのフレームについて誤り統計を収集します。

for counter = 1:100
   % Transmit 100 3-bit words
   data = randi([0 1],300,1);
   modSignal = gmskmodulator(data);
   noisySignal = channel(modSignal);
   receivedData = gmskdemodulator(noisySignal);
   errorStats = errorRate(data, receivedData);
end

誤りの統計を表示します。

fprintf('Error rate = %f\nNumber of errors = %d\n', ...
         errorStats(1), errorStats(2))

Error rate = 0.000133
Number of errors = 4

GMSK 変調される信号に対する帯域幅と時間の積による効果

ライブスクリプトを開く

この例は、GMSK 変調される信号に対する帯域幅と時間 (BT) の積による効果を説明しています。

バイナリデータのベクトルを作成し、このデータに GMSK 変調を適用します。

d = [0 1 1 0 1 0 0 1 1 1]';
a = comm.GMSKModulator(BitInput=true,SamplesPerSymbol=10)

a = 
  comm.GMSKModulator with properties:

                BitInput: true
    BandwidthTimeProduct: 0.3000
             PulseLength: 4
        SymbolPrehistory: 1
      InitialPhaseOffset: 0
        SamplesPerSymbol: 10
          OutputDataType: 'double'

x = a(d);
BTa = sprintf('BT=%2.1f',a.BandwidthTimeProduct);

位相角をプロットし、関数 unwrap を使用してトレンドをより適切に表示します。

plot(unwrap(angle(x)),'red-');
title('Bandwidth Time Product Effect')
hold on; 
plot(1:10:length(x),unwrap(angle(x(1:10:end))),'*');
grid on

BT 積を 1 に設定し、同じプロットで位相角をプロットします。

a = comm.GMSKModulator(BitInput=true, ...
    SamplesPerSymbol=10,BandwidthTimeProduct=1)

a = 
  comm.GMSKModulator with properties:

                BitInput: true
    BandwidthTimeProduct: 1
             PulseLength: 4
        SymbolPrehistory: 1
      InitialPhaseOffset: 0
        SamplesPerSymbol: 10
          OutputDataType: 'double'

x = a(d);
BTb = sprintf('BT=%2.1f',a.BandwidthTimeProduct);
plot(unwrap(angle(x)),'blue-.');
plot(1:10:length(x),unwrap(angle(x(1:10:end))),'o');

BT 積を 0.1 に設定し、同じプロットで位相角をプロットします。

a = comm.GMSKModulator(BitInput=true, ...
    SamplesPerSymbol=10,BandwidthTimeProduct=0.1)

a = 
  comm.GMSKModulator with properties:

                BitInput: true
    BandwidthTimeProduct: 0.1000
             PulseLength: 4
        SymbolPrehistory: 1
      InitialPhaseOffset: 0
        SamplesPerSymbol: 10
          OutputDataType: 'double'

BTc = sprintf('BT=%2.1f',a.BandwidthTimeProduct);

このパルスの拡散は BT 積に逆比例し、BT が小さくなるほど、ビットシンボル周期において拡散がより大きくなります。パルスのピーク振幅は BT 積に直接比例し、ピーク振幅が小さくなるほど、ビットシンボル周期において拡散がより小さくなります。パルスの帯域幅が減少するにつれ、パルス存続時間が長くなります。

x = a(d);
plot(unwrap(angle(x)),'green--');
plot(1:10:length(x),unwrap(angle(x(1:10:end))),'x');
legend(BTa,'',BTb,'',BTc,'')
hold off;

GMSK 変調と MSK 変調の比較

ライブスクリプトを開く

パルス長の異なるガウス最小偏移変調 (GMSK) および最小偏移変調 (MSK) のアイダイアグラムをプロットして GMSK および MSK の変調スキームを比較します。

シンボル変数あたりのサンプルを設定します。

sps = 8;

ランダムなバイナリデータを生成します。

data = randi([0 1],1000,1);

バイナリ入力を受け入れる GMSK 変調器および MSK 変調器を作成します。GMSK 変調器の PulseLength プロパティを 1 に設定します。

gmskMod = comm.GMSKModulator( ...
    BitInput=true, ...
    PulseLength=1, ...
    SamplesPerSymbol=sps);
mskMod = comm.MSKModulator( ...
    BitInput=true, ...
    SamplesPerSymbol=sps);

GMSK 変調器および MSK 変調器を使用してデータを変調します。

modSigGMSK = gmskMod(data);
modSigMSK = mskMod(data);

SNR が 30 dB の AWGN チャネル経由で変調信号を渡します。

rxSigGMSK = awgn(modSigGMSK,30);
rxSigMSK = awgn(modSigMSK,30);

関数eyediagramを使用して、ノイズを含む信号のアイダイアグラムをプロットします。GMSK パルスの長さを 1 に設定すると、アイダイアグラムはほぼ同じになります。

eyediagram(rxSigGMSK,sps,1,sps/2)

eyediagram(rxSigMSK,sps,1,sps/2)

GMSK 変調器オブジェクトの PulseLength プロパティを 3 に設定します。プロパティは調整不可能であるため、最初にオブジェクトを解放する必要があります。

release(gmskMod)
gmskMod.PulseLength = 3;

更新した GMSK 変調器オブジェクトを使用して変調信号を生成し、生成した変調信号を AWGN チャネル経由で渡します。

modSigGMSK = gmskMod(data);
rxSigGMSK = awgn(modSigGMSK,30);

GSMK などの連続位相変調 (CPM) 波形では、波形は前のシンボルや現在のシンボルの値に依存します。パルスの長さが長くなるとアイダイアグラムのパスの数が増加することを確認するために、GMSK 信号のアイダイアログラムをプロットします。

eyediagram(rxSigGMSK,sps,1,sps/2)

GMSK 変調器オブジェクトの PulseLength パラメーターを他の値に変更して実験できます。プロパティを偶数に設定した場合、変調信号をわかりやすく表示するために gmskMod.InitialPhaseOffset を pi/4 に、関数 eyediagram のオフセット引数を sps/2 から 0 に更新する必要があります。ガウスパルス整形をよりわかりやすく表示するには、View CPM Phase Tree Using Simulinkの例で説明したように、信号の位相を表示するスコープを使用しなければなりません。

アルゴリズム

BandwidthTimeProduct プロパティは、帯域幅と時間の積を表します。このプロパティを使用すると帯域幅が狭くなりますが、符号間干渉が増加します。PulseLength プロパティは、シンボル区間でのガウスパルス整形の長さを測定します。以下の方程式によって周波数パルス整形が定義されます。B_b はパルスの帯域幅を表し、T はシンボル区間を表します。Q(t) は相補累積分布関数です。

$\begin{array}{l} g (t) = \frac{1}{2 T} {Q [2 π B_{b} \frac{t - \frac{T}{2}}{\sqrt{\ln (2)}}] - Q [2 π B_{b} \frac{t + \frac{T}{2}}{\sqrt{\ln (2)}}]} \\ Q (t) = \int_{t}^{\infty} \frac{1}{\sqrt{2 π}} e^{- τ^{2} / 2} d τ \end{array}$

この System object では、1 の入力シンボルによって πp/2 ラジアンの位相シフトが生じます。これは、変調指数 0.5 に相当します。

参照

[1] Anderson, John B., Tor Aulin, and Carl-Erik Sundberg. Digital Phase Modulation. New York: Plenum Press, 1986.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

MATLAB コード生成における System object (MATLAB Coder)を参照してください。

バージョン履歴

R2012a で導入

すべて展開する

R2024a: 可変サイズのサポート

このサポートによって、オブジェクトを呼び出すたびに入力信号の長さを変えられるようになりました。

参考

オブジェクト

comm.CPFSKModulator | comm.CPFSKDemodulator | comm.GMSKDemodulator | comm.MSKModulator | comm.MSKDemodulator | comm.CPMModulator

ブロック

GMSK Modulator Baseband | GMSK Demodulator Baseband

comm.GMSKModulator

説明

作成

構文

説明

プロパティ

BitInput — 入力をビットとして提供するオプション false または 0 (既定値) | true または 1

BandwidthTimeProduct — 帯域幅とシンボル時間の積 0.3 (既定値) | 正のスカラー

PulseLength — パルス長 4 (既定値) | 正の整数

SymbolPrehistory — シンボル プレヒストリ 1 (既定値) | -1 | ベクトル

InitialPhaseOffset — 初期位相オフセット 0 (既定値) | 数値スカラー

SamplesPerSymbol — 出力シンボルあたりのサンプル数 8 (既定値) | 正の整数

OutputDataType — 出力のデータ型 'double' (既定値) | 'single'

使用法

構文

説明

入力引数

X — 入力データ 整数 | 列ベクトル

出力引数

Y — GMSK 変調されたベースバンド信号 ベクトル

オブジェクト関数

すべての System object に共通

例

バイナリ データの GMSK 信号へのマッピング

AWGN 環境下の GMSK 信号

GMSK 変調される信号に対する帯域幅と時間の積による効果

GMSK 変調と MSK 変調の比較

アルゴリズム

参照

拡張機能

C/C++ コード生成 MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2024a: 可変サイズのサポート

参考

オブジェクト

ブロック

`BitInput` — 入力をビットとして提供するオプション
`false` または `0` (既定値) | `true` または `1`

`BandwidthTimeProduct` — 帯域幅とシンボル時間の積
`0.3` (既定値) | 正のスカラー

`PulseLength` — パルス長
`4` (既定値) | 正の整数

`SymbolPrehistory` — シンボルプレヒストリ
`1` (既定値) | `-1` | ベクトル

`InitialPhaseOffset` — 初期位相オフセット
`0` (既定値) | 数値スカラー

`SamplesPerSymbol` — 出力シンボルあたりのサンプル数
`8` (既定値) | 正の整数

`OutputDataType` — 出力のデータ型
`'double'` (既定値) | `'single'`

`X` — 入力データ
整数 | 列ベクトル

`Y` — GMSK 変調されたベースバンド信号
ベクトル

バイナリデータの GMSK 信号へのマッピング

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。