wden
自動 1 次元ノイズ除去
wden は非推奨になりました。代わりに wdenoise を使用してください。
構文
説明
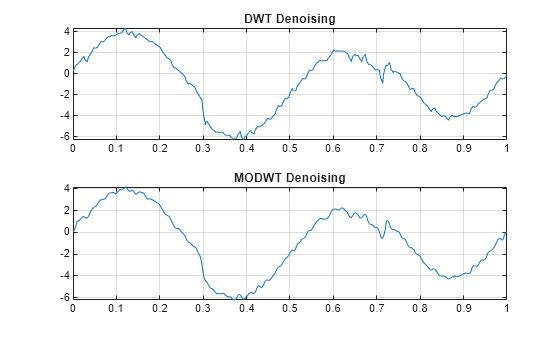
例
入力引数
出力引数
アルゴリズム
ノイズを含む信号の最も一般的なモデルは次の形式になります。
n は時間で、等間隔になります。この最も簡単なモデルにおいて、e(n) がガウス ホワイト ノイズ N(0,1) で、ノイズ レベル σ が 1 に等しいとします。ノイズ除去の目的は、信号 s のノイズ部分を抑制し、f を復元することです。
ノイズ除去手順には 3 つのステップがあります。
分解 — ウェーブレットを選択し、レベル
Nを選択します。信号 s のレベルNのウェーブレット分解を計算します。Detail 係数のしきい値処理 — 1 から
Nまでの各レベルで、しきい値を選択し、Detail 係数にソフトなしきい値処理を適用します。再構成 — レベル
Nの元の Approximation 係数とレベル 1 からNまでの変更後の Detail 係数に基づいて、ウェーブレットの再構成を計算します。
しきい値選択ルールの詳細については、Wavelet Denoising and Nonparametric Function Estimationおよび関数 thselect のヘルプを参照してください。次の点に注意してください。
Detail 係数ベクトルは、f の係数と e の係数の重ね合わせです。e の分解で得られる Detail 係数は、標準のガウス ホワイト ノイズです。
ミニマックスと SURE のしきい値選択ルールはより保守的であり、関数 f の小さな Detail がノイズ範囲にある場合に便利です。他の 2 つのルールはノイズをより効率的に除去します。オプション
'heursure'は折衷案です。
実際には、基本モデルを直接使用することはできません。モデルのずれに対処するため、残りのパラメーター scal を指定しなければなりません。これがしきい値の再スケーリング方法に対応します。
オプション
scal='one'は、基本モデルに対応します。オプション
scal = 'sln'は、第 1 レベルの係数に基づいたレベル ノイズの単一推定を使用して、しきい値の再スケーリングを処理します。一般に、推定しなければならないノイズ レベルは無視できます。Detail 係数 CD1 (最も細かいスケール) は、基本的に標準偏差が σ に等しいノイズ係数です。この係数の中央絶対偏差が、σ のロバスト推定です。ロバスト推定の使用は重要です。レベル 1 の係数に f の Detail が含まれる場合、これらの Detail は、信号終了の影響 (エッジでの演算による完全なアーティファクト) を避けるため、少数の係数に集められます。
オプション
scal='mln'は、そのレベル ノイズのレベル依存推定を使用して、しきい値の再スケーリングを処理します。非ホワイト ノイズ e が疑わしい場合、そのレベル ノイズのレベル依存推定によってしきい値を再スケーリングしなければなりません。同様の戦略を使用して、レベルごとに σlev レベルを推定します。この推定はファイル
wnoisestに実装されています。これは、元の信号 s のウェーブレット分解構造を直接処理します。
参照
[1] Antoniadis, A., and G. Oppenheim, eds. Wavelets and Statistics, 103. Lecture Notes in Statistics. New York: Springer Verlag, 1995.
[2] Donoho, D. L. “Progress in Wavelet Analysis and WVD: A Ten Minute Tour.” Progress in Wavelet Analysis and Applications (Y. Meyer, and S. Roques, eds.). Gif-sur-Yvette: Editions Frontières, 1993.
[3] Donoho, D. L., and Johnstone, I. M. “Ideal Spatial Adaptation by Wavelet Shrinkage.” Biometrika, Vol. 81, pp. 425–455, 1994.
[4] Donoho, D. L. “De-noising by Soft-Thresholding.” IEEE Transactions on Information Theory, Vol. 42, Number 3, pp. 613–627, 1995.
[5] Donoho, D. L., I. M. Johnstone, G. Kerkyacharian, and D. Picard. “Wavelet Shrinkage: Asymptopia?” Journal of the Royal Statistical Society, series B. Vol. 57, Number 2, pp. 301–369, 1995.
拡張機能
バージョン履歴
R2006a より前に導入