カメラ キャリブレーションとは

"幾何学的カメラ キャリブレーション" は "camera resectioning" とも呼ばれ、レンズおよびイメージまたはビデオ カメラのイメージ センサーのパラメーターを推定します。これらのパラメーターを使用して、レンズ歪みの修正や、オブジェクトのワールド単位でのサイズ測定、シーン内のカメラ位置の判定などを実行できます。これらのタスクはマシン ビジョンなどのアプリケーションでオブジェクトの検出と測定に使用されます。また、ロボティクスのナビゲーション システムや、3 次元シーン再構成などにも使用されます。

カメラのキャリブレーションを行うと、以下のようなことが可能になります。

カメラのパラメーターには内部パラメーター、外部パラメーターおよび歪み係数が含まれます。カメラのパラメーターを推定するには、3 次元ワールド ポイントとそれに対応する 2 次元のイメージ ポイントが必要です。こうした対応関係は、チェッカーボードのようなキャリブレーション パターンの複数のイメージを使用して取得できます。この対応関係を使用してカメラのパラメーターを求めます。カメラをキャリブレーションした後、以下の方法で、推定されたパラメーターの精度を評価できます。

• カメラの相対位置とキャリブレーション パターンのプロット

• 再投影誤差の計算。

• パラメーター推定誤差の計算。

カメラ キャリブレーターを使用してカメラのキャリブレーションを実行し、推定されたパラメーターの精度を評価します。

カメラ モデル

Computer Vision Toolbox™ には、ピンホール カメラ モデル用と魚眼カメラ モデル用のキャリブレーション アルゴリズムが含まれています。魚眼カメラ モデルで使用できる視野 (FOV) は 195 度までです。

ピンホール キャリブレーション アルゴリズムは、Jean-Yves Bouguet [3]により提唱されたモデルに基づいています。このモデルには、ピンホール カメラ モデル [1] とレンズ歪み [2] が含まれています。典型的なピンホール カメラにはレンズがないため、ピンホール カメラ モデルではレンズ歪みが考慮されません。実際のカメラを正確に表すため、アルゴリズムで使用される完全なカメラ モデルには半径方向および円周方向のレンズ歪みが含まれます。

魚眼レンズが生成する極端な歪みのため、ピンホール モデルは魚眼カメラをモデル化できません。魚眼モデルを使用したカメラ キャリブレーションの詳細については、魚眼キャリブレーションの基礎を参照してください。

ピンホール カメラ モデル

ピンホール カメラはレンズがなく、小さな開口部が 1 つあるシンプルなカメラです。光線が開口部を通ってカメラの反対側に反転イメージとして投影されます。シーンの正立イメージを含むバーチャル イメージ平面がカメラの前にあると想定してください。

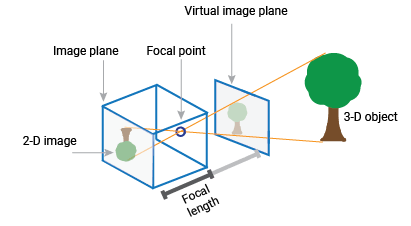
ピンホール カメラのパラメーターは "カメラ行列" と呼ばれる 3 行 4 列の行列で表されます。この行列は 3 次元世界のシーンをイメージ平面にマッピングします。キャリブレーション アルゴリズムは、カメラの外部パラメーターと内部パラメーターを使用してカメラ行列を計算します。外部パラメーターは 3 次元シーンにおけるカメラの位置を表します。内部パラメーターはカメラの光学的中心と焦点距離を表します。

ワールド ポイントは、外部パラメーターを使ってカメラ座標に変換されます。カメラ座標は内部パラメーターを使ってイメージ平面にマッピングされます。

カメラのキャリブレーション パラメーター

キャリブレーション アルゴリズムは、カメラの外部パラメーターと内部パラメーターを使用してカメラ行列を計算します。外部パラメーターは、3 次元のワールド座標系から 3 次元のカメラ座標系への剛体変換を表します。内部パラメーターは、3 次元のカメラ座標から 2 次元のイメージ座標への射影変換を表します。

外部パラメーター

外部パラメーターは、回転 R と変換 t で構成されています。カメラの座標系の原点はその光学的中心にあり、x- 軸と y- 軸でイメージ平面が定義されます。

内部パラメーター

内部パラメーターには、焦点距離、光学的中心 ("主点" とも呼ばれます) およびせん断係数が含まれます。カメラの内部パラメーターの行列 K は次のように定義されます。

$$\left[\begin{array}{ccc}{f}_x& s& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

ピクセルせん断は次のように定義されます。

$$\left[\begin{array}{cc}{c}_x& c_y\end{array}\right]$$ — ピクセル単位の光学的中心 (主点)。

$$\left(\begin{array}{cc}{f}_x,& f_y\end{array}\right)$$ — ピクセル単位の焦点距離。 $$f_x=F/p_x$$ $$f_y=F/p_y$$ $$F$$ — ワールド単位の焦点距離で、通常はミリメートル単位で表されます。 $$\left(\begin{array}{cc}{p}_x,& p_y\end{array}\right)$$ — ワールド単位のピクセルのサイズ。

$$s$$ — せん断係数。イメージの座標軸が直交しない場合は非ゼロです。 $$s=f_x\tan \alpha$$

カメラ キャリブレーションの歪み

典型的なピンホール カメラにはレンズがないため、カメラ行列ではレンズ歪みが考慮されません。実際のカメラを正確に表現するために、カメラ モデルには半径方向および円周方向のレンズ歪みが含まれています。

半径方向の歪み

半径方向の歪みは、レンズの光学的中心からエッジに向かうにつれて光線の屈折率が大きくなる現象を指しています。この歪みはレンズが小さいほど大きくなります。

半径方向の歪み係数は、このタイプの歪みをモデル化します。歪んだ点は (x_distorted, y_distorted) として次のように表されます。

x_distorted = x(1 + k₁*r² + k₂*r⁴ + k₃*r⁶)

y_distorted= y(1 + k₁*r² + k₂*r⁴ + k₃*r⁶)

• x、y — 歪み補正後のピクセル位置。x と y は正規化されたイメージ座標内にあります。正規化されたイメージ座標は、光学的中心への変換後にピクセル単位の焦点距離で除算したピクセル座標から求められます。したがって、x と y は次元がありません。

• k₁、k₂ および k₃ — レンズの半径方向の歪み係数。

• r² = x² + y²

一般に、キャリブレーションを行うには 2 つの係数で十分です。広角レンズなどの歪みが大きい場合には、3 つの係数を選択して k₃ を含めることができます。

円周方向の歪み

円周方向の歪みは、レンズとイメージ平面が平行にならない場合に生じます。円周方向の歪み係数は、このタイプの歪みをモデル化します。

歪んだ点は (x_distorted, y_distorted) として次のように表されます。

x_distorted = x + [2 * p₁ * x * y + p₂ * (r² + 2 * x²)]

y_distorted = y + [p₁ * (r² + 2 *y²) + 2 * p₂ * x * y]

• x、y — 歪み補正後のピクセル位置。x と y は正規化されたイメージ座標内にあります。正規化されたイメージ座標は、光学的中心への変換後にピクセル単位の焦点距離で除算したピクセル座標から求められます。したがって、x と y は次元がありません。

• p₁ および p₂ — レンズの円周方向の歪み係数。

• r² = x² + y²

参照

[1] Zhang, Z. “A Flexible New Technique for Camera Calibration.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 22, No. 11, 2000, pp. 1330–1334.

[2] Heikkila, J., and O. Silven. “A Four-step Camera Calibration Procedure with Implicit Image Correction.” IEEE International Conference on Computer Vision and Pattern Recognition.1997.

[3] Bouguet, J. Y. “Camera Calibration Toolbox for Matlab.” Computational Vision at the California Institute of Technology.

[4] Bradski, G., and A. Kaehler. Learning OpenCV: Computer Vision with the OpenCV Library. Sebastopol, CA: O'Reilly, 2008.

参考

アプリ

• カメラ キャリブレーター | ステレオ カメラ キャリブレーター

関連するトピック

• MATLAB での Visual SLAM の実装
• 単一カメラ キャリブレーター アプリの使用
• ステレオ カメラ キャリブレーター アプリの使用
• 単一カメラのキャリブレーションの精度の評価
• 魚眼キャリブレーションの基礎
• 単眼魚眼カメラの構成 (Automated Driving Toolbox)
• 単眼カメラのキャリブレーション (Automated Driving Toolbox)
• キャリブレートされたカメラによる平面オブジェクトの測定
• 2 つのビューからの structure from motion
• 複数のビューからの structure from motion