カテゴリカル共変量による線形回帰

この例では、categorical 配列と fitlm を使用してカテゴリカル共変量による回帰を実行する方法を説明します。

標本データを読み込みます。

load carsmall

変数 MPG には、100 台の標本の自動車について、ガロンあたりの走行マイル数の測定値が格納されています。それぞれの自動車のモデル年は変数 Model_Year に格納されています。また、Weight にはそれぞれの自動車の重量が格納されています。

グループ化されたデータをプロットします。

Weight に対する MPG の散布図をモデル年別に作成します。

figure()
gscatter(Weight,MPG,Model_Year,'bgr','x.o')
title('MPG vs. Weight, Grouped by Model Year')

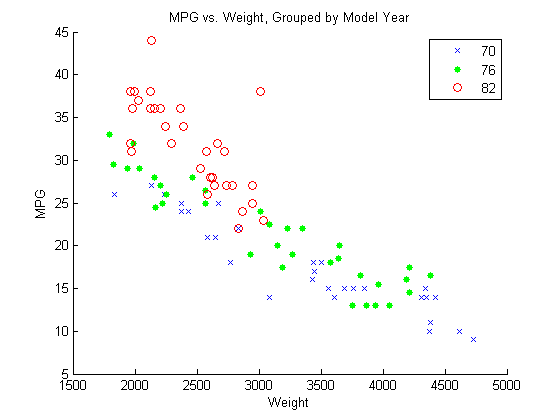
Scatter plot of MPG versus Weight. The observations are grouped by model year. Observations corresponding to 1970, 1976, and 1982 are plotted as blue X markers, green points, and red O markers, respectively.

グループ化変数 Model_Year には、70、76、82 の 3 つの一意の値が含まれており、それぞれ 1970 年、1976 年、1982 年のモデル年に対応しています。

テーブルと categorical 配列を作成します。

変数 MPG、Weight、Model_Year を格納するテーブルを作成します。変数 Model_Year を categorical 配列に変換します。

cars = table(MPG,Weight,Model_Year);
cars.Model_Year = categorical(cars.Model_Year);

非線形回帰モデルを当てはめます。

fitlm で MPG を従属変数、Weight と Model_Year を独立変数として使用し、回帰モデルを当てはめます。Model_Year は 3 つの水準をもつカテゴリカル共変量なので、2 つの指標変数としてモデルを入力する必要があります。

この散布図を見ると、Weight に対する MPG の傾きはモデル年によって違いがありそうです。これを評価するには、重量と年の交互作用項を使用します。

推奨されるモデルは次のとおりです。

$E (M P G) = β_{0} + β_{1} W e i g h t + β_{2} I [1976] + β_{3} I [1982] + β_{4} W e i g h t \times I [1976] + β_{5} W e i g h t \times I [1982],$

ここで、I[1976] と I[1982] はそれぞれ 1976 年および 1982 年というモデル年を表すダミー変数です。I[1976] の値は、モデル年が 1976 の場合は 1、そうでない場合は 0 になります。I[1982] の値は、モデル年が 1982 の場合は 1、そうでない場合は 0 になります。このモデルでは、1970 年が基準の年となります。

fit = fitlm(cars,'MPG~Weight*Model_Year')

fit = 


Linear regression model:
    MPG ~ 1 + Weight*Model_Year

Estimated Coefficients:
                             Estimate          SE    
                            ___________    __________

    (Intercept)                  37.399        2.1466
    Weight                   -0.0058437    0.00061765
    Model_Year_76                4.6903        2.8538
    Model_Year_82                21.051         4.157
    Weight:Model_Year_76    -0.00082009    0.00085468
    Weight:Model_Year_82     -0.0050551     0.0015636


                             tStat        pValue  
                            ________    __________

    (Intercept)               17.423    2.8607e-30
    Weight                   -9.4612    4.6077e-15
    Model_Year_76             1.6435       0.10384
    Model_Year_82             5.0641    2.2364e-06
    Weight:Model_Year_76    -0.95953       0.33992
    Weight:Model_Year_82     -3.2329     0.0017256


Number of observations: 94, Error degrees of freedom: 88
Root Mean Squared Error: 2.79
R-squared: 0.886,  Adjusted R-Squared: 0.88
F-statistic vs. constant model: 137, p-value = 5.79e-40

この回帰モデルからは次のことがわかります。

fitlm は Model_Year をカテゴリカル変数として認識し、必要な指標 (ダミー) 変数を作成します。既定では、最初の水準 70 が参照グループとなります (reordercats を使用すると参照グループを変更できます)。
モデルの仕様 MPG~Weight*Model_Year では、Weight と Model_Year の 1 次項と、すべての交互作用が指定されています。
モデル R² = 0.886 とは、重量とモデル年、さらに両者の交互作用を考慮した場合、ガロンあたりの走行マイル数の変動が 88.6% 縮小することを意味します。
当てはめたモデルは次のようになります。

$M \hat{P} G = 37.4 - 0.006 W e i g h t + 4.7 I [1976] + 21.1 I [1982] - 0.0008 W e i g h t \times I [1976] - 0.005 W e i g h t \times I [1982] .$
これにより、モデル年に関して次の回帰方程式が推定されます。
モデル年重量に対して予測される MPG
1970

$M \hat{P} G = 37.4 - 0.006 W e i g h t$

1976

$M \hat{P} G = (37.4 + 4.7) - (0.006 + 0.0008) W e i g h t$

1982

$M \hat{P} G = (37.4 + 21.1) - (0.006 + 0.005) W e i g h t$

モデル年	重量に対して予測される MPG
1970	$M \hat{P} G = 37.4 - 0.006 W e i g h t$
1976	$M \hat{P} G = (37.4 + 4.7) - (0.006 + 0.0008) W e i g h t$
1982	$M \hat{P} G = (37.4 + 21.1) - (0.006 + 0.005) W e i g h t$

MPG と Weight の間の関係は、モデル年が後になるほど負の傾きが大きくなります。

近似回帰直線をプロットします。

データと近似回帰線をプロットします。

w = linspace(min(Weight),max(Weight));

figure()
gscatter(Weight,MPG,Model_Year,'bgr','x.o')
line(w,feval(fit,w,'70'),'Color','b','LineWidth',2)
line(w,feval(fit,w,'76'),'Color','g','LineWidth',2)
line(w,feval(fit,w,'82'),'Color','r','LineWidth',2)
title('Fitted Regression Lines by Model Year')

さまざまな傾きにテストを行います。

傾き間の有意差に関するテストを行います。これは、次の仮説の検定と等価です。

$\begin{array}{l} H_{0} : β_{4} = β_{5} = 0 \\ H_{A} : β_{i} \neq 0 for at least one i . \end{array}$

anova(fit)

ans = 

                         SumSq     DF    MeanSq    F         pValue    
    Weight               2050.2     1    2050.2    263.87    3.2055e-28
    Model_Year           807.69     2    403.84    51.976    1.2494e-15
    Weight:Model_Year    81.219     2    40.609    5.2266     0.0071637
    Error                683.74    88    7.7698

この出力結果から、この検定での p 値が 0.0072 (交互作用行 Weight:Model_Year) であることがわかります。つまり、帰無仮説は有意水準 0.05 で棄却されます。検定統計量の値は 5.2266 です。この検定での分子の自由度は 2 です。これは帰無仮説での係数の数です。

3 つのモデル年のすべてで傾きが等しいわけではないという十分な証拠が示されました。

参考

fitlm | categorical | reordercats | anova