柔軟な分布族を使用してデータを生成

この例では、ピアソンおよびジョンソン分布システムを使用してデータを生成する方法を示します。

ピアソン システムおよびジョンソン システム

確率分布の操作で説明されたように、データをモデル化するために分布のパラメーター族を適切に選択する際、データ生成プロセスの "事前"または ”事後”の知識をベースすることができます。しかし、この選択は容易ではありません。"ピアソンおよびジョンソンのシステム" により、そのような選択を不要にできます。どちらも分布形状が広範囲な、柔軟な分布パラメーター族であり、これら 2 つのシステムのいずれかのうちに、データによく一致する分布が検出できます。

データ入力

以下のパラメーターはピアソンおよびジョンソン システムの各メンバーを定義します。

• 平均 — mean により推定されます。

• 標準偏差 — std により推定されます。

• 歪度 — skewness により推定されます。

• 尖度 — kurtosis により推定されます。

これらの統計は、関数 moment を使用して計算することもできます。ジョンソン システムはこれらの 4 つのパラメーターに基づいていますが、関数quantileによって推定される分位数を使用すると、より自然に記述されます。

関数 pearsrndおよびjohnsrnd は、分布を定義する入力引数 (それぞれパラメーターまたは分位数) を受け入れ、対応するシステムにおける分布のタイプと係数を返します。また、関数は両方とも、指定の分布から乱数を生成することができます。

例として、各自動車に対する燃費効率の測定を含む変数 MPG を含む、carbig.mat にデータを読み込んでください。

load carbig
MPG = MPG(~isnan(MPG));
histogram(MPG,15)

以下の 2 つの節では、それぞれピアソンおよびジョンソンのシステムのメンバーをもつ分布をモデルにします。

ピアソン システムを使用したデータの生成

統計学者 Karl Pearson は、平均、標準偏差、歪度、尖度の適切な各組み合わせに対応する一意的な分布を含む、分布のシステムすなわち分布族を考案しました。データからこれらの各モーメントの標本の値を計算する場合、ピアソン システムを使うことで、これら 4 つのモーメントに一致する分布を検出すると、無作為標本を容易に生成できます。

ピアソン システムでは、7 つの基本タイプの分布が一緒に 1 つのパラメトリックな枠組みに組み込まれています。これには、一般的な分布 (正規分布や $$t$$ 分布など)、標準分布の簡単な変換 (シフトおよびスケーリングされたベータ分布や逆ガンマ分布など)、および標準分布の単純な変換ではない 1 つの分布 (タイプ IV) が含まれます。

取得されたモーメントの組み合わせに対して、最初の 4 つのモーメントが同じであっても、システムにない分布があります。さらに、特に、データが多様である場合、ピアソン システムの分布はデータをうまく近似しないことがあります。しかし、システムは、対称分布と非対称分布の両方を含み、広範囲の分布形状をカバーします。

MPG データと厳密に一致するピアソン分布から標本を生成するには、単に、4 つの標本モーメントを計算し、これらを分布のパラメーターとして取り扱います。

moments = {mean(MPG),std(MPG),skewness(MPG),kurtosis(MPG)};
rng('default')  % For reproducibility
[r,type] = pearsrnd(moments{:},10000,1);

pearsrnd による 2 番目の出力 (オプション) は、ピアソン システム内のどのタイプの分布がモーメントの組み合わせに一致するかを示します。

type

type = 1

この場合、pearsrnd は、シフトとスケールされたベータ分布である、タイプ I のピアソン分布でデータがよく記述されることを判定しました。

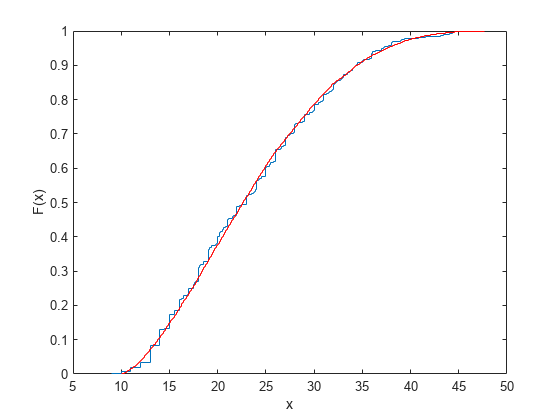
経験的累積分布関数を重ね書きし、標本がオリジナルのデータに似ていることを確かめてください。

ecdf(MPG);
[Fi,xi] = ecdf(r);
hold on;
stairs(xi,Fi,'r');
hold off

ジョンソン システムを使用したデータの生成

統計学者 Norman Johnson はこれとは別の、平均、標準偏差、歪度、尖度のあらゆる有効な組み合わせに対応する固有の分布も含む、分布システムを考案しました。ただし、分位数を使ってジョンソン システムの分布を記述する方がより自然である点において、このシステムでの処理はピアソン システムによる処理とは異なります。

ジョンソン システムは、1 つの正規確率変数が取り得る 3 つの変換、それに加えての恒等変換に基づきます。重要な 3 つの変換は SL、SU、SB として知られ、それぞれ、指数、ロジスティック、双曲正弦変換に対応します。この 3 つはすべて次のように記述できます。

$$X=\gamma +\delta \cdot \Gamma \left(\frac{Z-\xi }{\lambda }\right)$$

ここで、$$Z$$ は標準正規確率変数、$$\Gamma$$ は変換、$$\gamma$$、$$\delta$$、$$\xi$$ および $$\lambda$$ はスケール パラメーターと位置パラメーターです。4 番目の変換 SN は、恒等変換です。

MPG データに一致するジョンソン 分布から標本を作成するには、まず 4 つの分位数を、4 つの等間隔の標準正規分位数 -1.5、-0.5、0.5、1.5 から変換して定義します。つまり、0.067、0.309、0.691、0.933 の累積確率に対して、データの標本分位数を計算します。

probs = normcdf([-1.5 -0.5 0.5 1.5])

probs = 1×4

    0.0668    0.3085    0.6915    0.9332

quantiles = quantile(MPG,probs)

quantiles = 1×4

   13.0000   18.0000   27.2000   36.0000

その後、それらの分位数を分布パラメーターとして扱います。

[r1,type] = johnsrnd(quantiles,10000,1);

johnsrnd による 2 番目の出力 (オプション) は、ジョンソン システム内のどのタイプの分布が分位数に一致するかを示します。

type

type = 
'SB'

経験的累積分布関数を重ね書きすることによって、標本がオリジナルのデータに似ていることを確かめることができます。

ecdf(MPG);
[Fi,xi] = ecdf(r1);
hold on;
stairs(xi,Fi,'r');
hold off

用途によっては、ある領域内での分位数が他の領域内のものよりも良く一致することが重要な場合があります。そのためには、データを一致させたい位置に、既定の -1.5、-0.5、0.5、1.5 の代わりに 4 つの等間隔の標準正規分位数を指定します。たとえば、左の裾ではなく右の裾のデータでの一致を、より重要と考えるかもしれません。その場合、右の裾を重視して標準正規分布する分位数を指定します。

qnorm = [-.5 .25 1 1.75];
probs = normcdf(qnorm);
qemp = quantile(MPG,probs);
r2 = johnsrnd([qnorm; qemp],10000,1);

しかし、新しい標本は右の裾ではオリジナルのデータにより良く一致しますが、左の裾ではずっと悪くなっています。

[Fj,xj] = ecdf(r2);
hold on;
stairs(xj,Fj,'g');
hold off

参考

pearsrnd | johnsrnd | ecdf