johnsrnd

ジョンソン システム乱数

構文

r = johnsrnd(quantiles,m,n)
r = johnsrnd(quantiles)
[r,type] = johnsrnd(...)
[r,type,coefs] = johnsrnd(...)


説明

r = johnsrnd(quantiles,m,n) は、quantiles で与えられた分位数指定を満たすジョンソン システム分布から取り出した m 行 n 列の乱数行列を返します。quantiles は、標準正規分位数 [–1.5 –0.5 0.5 1.5] に対応する目的の分布の分位数の 4 要素ベクトルです。言い換えると、[0.067 0.309 0.691 0.933] という累積確率に対応する分位数を指定することにより、乱数値の抽出元となる分布を指定します。quantiles は、4 つの標準正規分位数が 1 行目に、目的の分布における対応する分位数が 2 行目に含まれている 2 行 4 列の行列にすることもできます。標準正規分位数は、等間隔でなければなりません。

メモ

r は、無作為標本であるため、通常、その標本分位数は指定された分布分位数とは若干異なります。

r = johnsrnd(quantiles) は、スカラー値を返します。

r = johnsrnd(quantiles,m,n,...) または r = johnsrnd(quantiles,[m,n,...]) は、m x n x ... の配列を返します。

[r,type] = johnsrnd(...) は、ジョンソン システム内の指定された分布のタイプを返します。type は 'SN'、'SL'、'SB' または 'SU' です。m と n をゼロに設定すると、乱数値を生成せずに分布タイプを識別できます。

ジョンソン システムの 4 つの分布タイプは、正規確率変量の以下の変化に対応します。

• 'SN' — 恒等変換 (正規分布)

• 'SL' — 指数変換 (対数正規分布)

• 'SB' — ロジスティック変換 (有界)

• 'SU' — 双曲正弦変換 (非有界)

[r,type,coefs] = johnsrnd(...) は、分布を定義する変換の係数 coefs を返します。coefs は、[gamma, eta, epsilon, lambda] です。z が標準正規分布に従う確率変数で h が上記で定義される変換のいずれかである場合、r = lambda*h((z-gamma)/eta)+epsilon は、h に対応する分布タイプからの確率変量です。

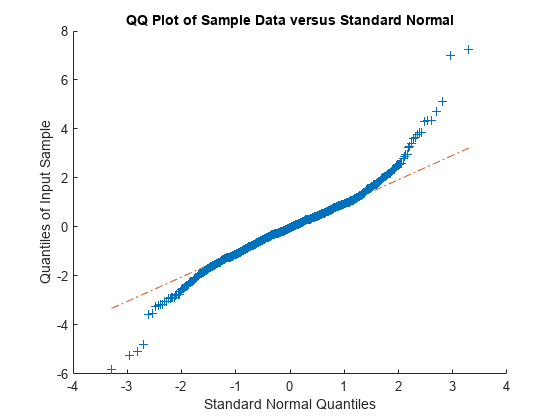
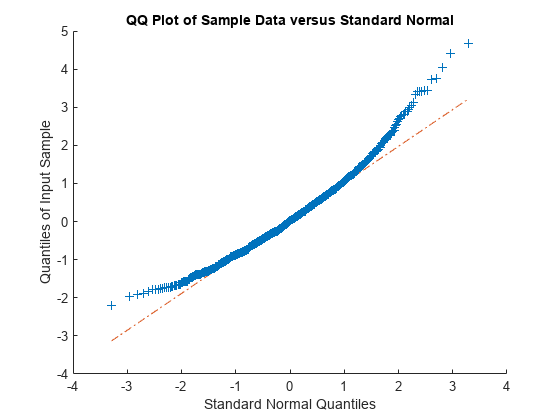
例

ジョンソン システムを使用した無作為標本の生成

この例では、柔軟な分布族から成るジョンソン システムを使用した、乱数発生および分布の標本データへの当てはめにおけるさまざまな手法を説明します。

標準正規分布より長い裾のある乱数値を生成します。

rng default;  % For reproducibility
r = johnsrnd([-1.7 -.5 .5 1.7],1000,1);
figure;
qqplot(r);

右側に偏った乱数値を生成します。

r = johnsrnd([-1.3 -.5 .5 1.7],1000,1);
figure;
qqplot(r);

標本データが右側の裾で一致する乱数値を生成します。

load carbig;
qnorm = [.5 1 1.5 2];
q = quantile(Acceleration, normcdf(qnorm));
r = johnsrnd([qnorm;q],1000,1);
[q;quantile(r,normcdf(qnorm))]

ans = 2×4

   16.7000   18.2086   19.5376   21.7263
   16.6986   18.2220   19.9078   22.0918

分布タイプと係数を決定します。

[r,type,coefs] = johnsrnd([qnorm;q],0)

r =

     []

type = 
'SU'

coefs = 1×4

    1.0920    0.5829   18.4382    1.4494

参照

[1] Johnson, Norman Lloyd, et al. Continuous Univariate Distributions. 2nd ed, Wiley 1994.

[2] Johnson, N. L. "Systems of Frequency Curves Generated by Methods of Translation." Biometrika 36, no. 1–2, Jun. 1949, 149–176.

[3] Slifker, James F., and Samuel S. Shapiro. "The Johnson System: Selection and Parameter Estimation." Technometrics 22, no. 2, May 1980, 239–246.

[4] Wheeler, Robert E. "Quantile Estimators of Johnson Curve Parameters." Biometrika 67, no. 3, Dec .1980, 725–728.

バージョン履歴

R2006a で導入

参考

random | pearsrnd

トピック

• 柔軟な分布族を使用してデータを生成