std
標準偏差
構文
説明
S = std(A)A の要素の標準偏差を返します。既定では標準偏差が N-1 で正規化されます。N は観測値の数です。
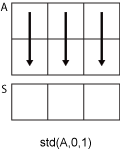
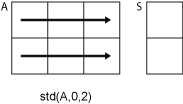
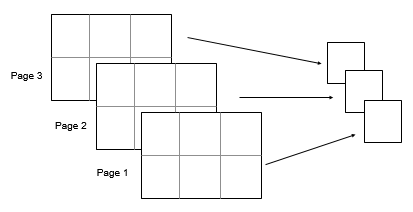
Aが観測値のベクトルである場合、Sはスカラーです。Aが、列に確率変数をもち、行に観測値をもつ行列である場合、Sは各列に対応する標準偏差を含む行ベクトルになります。Aが多次元配列の場合、std(A)は、サイズが 1 でない最初の配列次元に沿って演算します。要素はベクトルとして扱われます。この次元におけるSのサイズは1になりますが、他のすべての次元のサイズはAと同じです。Aがスカラーの場合、Sは0です。Aが0行0列の空の配列である場合、SはNaNです。Aが table または timetable の場合、std(A)は、各変数の標準偏差を含む 1 行の table を返します。 (R2023a 以降)
S = std(___,missingflag)A の欠損値を含めるか省略するかを指定します。たとえば、std(A,"omitmissing") は標準偏差の計算時にすべての欠損値を無視します。既定では、std は欠損値を含めます。