mean

配列の平均値

構文

M = mean(A)

M = mean(A,'all')

M = mean(A,dim)

M = mean(A,vecdim)

M = mean(___,outtype)

M = mean(___,nanflag)

説明

M = mean(A) は、サイズが 1 ではない最初の配列の次元に沿った A の要素の平均値を返します。

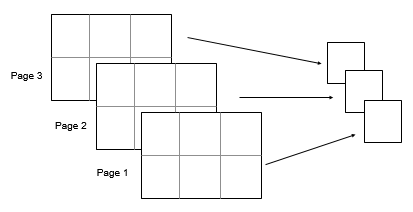
• A がベクトルの場合、mean(A) は要素の平均値を返します。

• A が行列の場合、mean(A) は各列の平均値を含む行ベクトルを返します。

• A が多次元配列の場合、mean(A) は、サイズが 1 でない最初の配列次元に対して作用します。ここでは要素をベクトルとして扱います。この次元のサイズは 1 になりますが、他のすべての次元のサイズは A と同じままです。

M = mean(A,'all') は、A のすべての要素の平均値を計算します。この構文は、MATLAB^® R2018b 以降で有効です。

M = mean(A,dim) は、次元 dim に沿って平均値を返します。たとえば、A が行列の場合、mean(A,2) は各行の平均値をもつ列ベクトルになります。

M = mean(A,vecdim) は、ベクトル vecdim で指定した次元に基づいて平均値を計算します。たとえば、A が行列の場合、mean(A,[1 2]) は、A 内のすべての要素の平均値になります。これは、行列のすべての要素が次元 1 と 2 で定義された配列スライスに含まれるためです。

M = mean(___,outtype) は前述の構文の入力引数のいずれかを使って、指定されたデータ型で平均値を返します。outtype は 'default'、'double' または 'native' になります。

M = mean(___,nanflag) は、前述の任意の構文について NaN 値を計算に含めるか省略するかを指定します。mean(A,'includenan') ではすべての NaN 値が計算に含められ、mean(A,'omitnan') ではこれらが無視されます。

例

行列の列の平均値

行列を作成して各列の平均値を計算します。

A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]

A = 4×3

     0     1     1
     2     3     2
     1     3     2
     4     2     2

M = mean(A)

M = 1×3

    1.7500    2.2500    1.7500

行列の行の平均値

行列を作成して各行の平均値を計算します。

A = [0 1 1; 2 3 2; 3 0 1; 1 2 3]

A = 4×3

     0     1     1
     2     3     2
     3     0     1
     1     2     3

M = mean(A,2)

M = 4×1

    0.6667
    2.3333
    1.3333
    2.0000

3 次元配列の平均値

1 ～ 10 の整数値の 4 x 2 x 3 の配列を作成し、2 番目の次元に沿って平均値を計算します。

rng('default')
A = randi(10,[4,2,3]);
M = mean(A,2)

M = 
M(:,:,1) =

    8.0000
    5.5000
    2.5000
    8.0000


M(:,:,2) =

   10.0000
    7.5000
    5.5000
    6.0000


M(:,:,3) =

    6.0000
    5.5000
    8.5000
   10.0000

配列ページの平均値

3 次元配列を作成し、データの各ページ (行と列) ごとの平均値を計算します。

A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [9 13; -5 7];
A(:,:,3) = [4 4; 8 -3];
M1 = mean(A,[1 2])

M1 = 
M1(:,:,1) =

    1.2500


M1(:,:,2) =

     6


M1(:,:,3) =

    3.2500

R2018b 以降、配列のすべての次元の平均値を計算するには、ベクトルの次元引数で各次元を指定するか、'all' オプションを使用します。

M2 = mean(A,[1 2 3])

M2 = 3.5000

Mall = mean(A,'all')

Mall = 3.5000

単精度配列の平均値

1 の単精度ベクトルを作成し、その単精度平均値を計算します。

A = single(ones(10,1));
M = mean(A,'native')

M = single
    1

結果も単精度になります。

class(M)

ans = 
'single'

NaN を除外した平均値

ベクトルを作成し、NaN 値を除いて平均値を計算します。

A = [1 0 0 1 NaN 1 NaN 0];
M = mean(A,'omitnan')

M = 0.5000

'omitnan' を指定しない場合、mean(A) は NaN を返します。

入力引数

A — 入力配列

ベクトル | 行列 | 多次元配列

入力配列。ベクトル、行列または多次元配列として指定します。

• A がスカラーの場合、mean(A) は A を返します。

• A が 0 行 0 列の空の行列である場合、mean(A) は NaN を返します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | datetime | duration

dim — 演算の対象の次元

正の整数スカラー

演算の対象の次元。正の整数のスカラーとして指定します。次元を指定しない場合、既定値はサイズが 1 より大きい最初の配列次元です。

次元 dim は、長さが 1 に縮小した次元を示します。size(M,dim) は 1 ですが、他のすべての次元のサイズは変化しません。

m 行 n 列の入力行列 A を考えます。

• mean(A,1) は、A の各列における要素の平均値を計算し、1 行 n 列の行ベクトルを返します。

  

• mean(A,2) は、A の各行における要素の平均値を計算し、m 行 1 列の列ベクトルを返します。

  

mean は、dim が ndims(A) より大きいか、size(A,dim) が 1 である場合に A を返します。

vecdim — 次元のベクトル

正の整数のベクトル

次元のベクトル。正の整数のベクトルとして指定します。各要素は入力配列の次元を表します。指定された操作次元の出力の長さは 1 で、その他は同じままです。

2 x 3 x 3 の入力配列 A を考えます。mean(A,[1 2]) は 1 x 1 x 3 の配列を返します。この配列の要素は、A の各ページの平均値です。

outtype — 出力データ型

'default' (既定値) | 'double' | 'native'

出力データ型。'default'、'double' または 'native' として指定します。これらのオプションにより、演算の実行に使用されるデータ型も指定されます。

outtype	出力データ型
'default'	double。ただし、入力データ型が single、duration または datetime の場合は出力が 'native' になります。
'double'	double。ただし、データ型が duration または datetime の場合、'double' はサポートされません。
'native'	次の場合を除き、入力と同じデータ型 入力データ型が double の場合、出力は logical になります。 入力データ型が char の場合、'native' はサポートされません。

データ型: char

nanflag — NaN の条件

'includenan' (既定値) | 'omitnan'

NaN の条件。次の値のいずれかとして指定します。

• 'includenan' — 平均値の計算に NaN 値を含めます。計算結果は NaN になります。

• 'omitnan' — 入力にあるすべての NaN 値を無視します。

datetime 配列では、'omitnat' を使用して NaT 値を省略し、あるいは 'includenat' を使用して同値を含めることができます。

詳細

平均

N 個のスカラー観測値からなる有限長ベクトル A の平均は、次のように定義されます。

$$\mu =\frac{1}{N}{\displaystyle \sum _{i=1}^N{A}_i}.$$

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

この関数は tall 配列を完全にサポートしています。詳細については、tall 配列を参照してください。

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• dim を指定する場合、定数でなければなりません。

• outtype オプションと nanflag オプションは定数の文字ベクトルでなければなりません。

• 整数型は 'native' 出力データ型オプションをサポートしません。

• ツールボックス関数のコード生成に対する可変サイズの制限 (MATLAB Coder)を参照してください。

GPU コード生成

GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

使用上の注意事項および制限事項:

• dim を指定する場合、定数でなければなりません。

• outtype オプションと nanflag オプションは定数の文字ベクトルでなければなりません。

• 整数型は 'native' 出力データ型オプションをサポートしません。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意事項および制限事項:

• 'native' オプションはサポートされていません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意事項および制限事項:

• 'native' オプションはサポートされていません。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

median | mode | std | var | sum

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい