アンサンブル分類における不均衡データまたは一様ではない誤分類コストの処理
多くの応用で、データのクラスを非対称的に処理したい場合があります。たとえば、あるクラスの観測値が他のクラスよりはるかに多くデータに含まれている場合があります。また、あるクラスの観測値を誤分類すると、別のクラスの観測値を誤分類する場合より深刻な結果になることもあります。このような場合は、RUSBoost アルゴリズムを使用 ('Method' として 'RUSBoost' を指定) するか、fitcensemble の名前と値のペアの引数 'Prior' または 'Cost' を使用できます。
過小または過大に表現されているクラスが学習セットに含まれている場合は、名前と値のペアの引数 'Prior' または RUSBoost アルゴリズムを使用します。たとえば、シミュレーションによって学習データを取得するとします。クラス A のシミュレートはクラス B のシミュレートより計算負荷が高いので、クラス A の観測値は少なく、クラス B の観測値は多く生成することにします。しかし、実際の (シミュレートしたのではない) 状況では、クラス A とクラス B の混合比率が異なると考えられます。このようなケースでは、'Prior' を使用して、実際の状況で観測されると考えられる値に近づくようにクラス A および B の事前確率を設定します。関数 fitcensemble は、合計が 1 になるように事前確率を正規化します。すべての事前確率に同じ正の係数を乗算しても、分類の結果に影響はありません。不均衡なデータを処理する方法には、RUSBoost アルゴリズム ('Method','RUSBoost'
学習データでは適切に表現されているクラスを非対称的に処理するには、名前と値のペアの引数 'Cost' を使用します。癌患者の良性腫瘍と悪性腫瘍を分類したいとします。悪性腫瘍の特定に失敗すること (偽陰性) は、良性を悪性と誤診する (偽陽性) よりも深刻な結果をもたらします。悪性を良性と誤診する場合には高いコストを、良性を悪性と誤診する場合には低いコストを割り当てなければならないはずです。
誤分類のコストは、非負の要素をもつ正方行列として渡さなければなりません。この行列の要素 C(i,j) は、真のクラスが i である場合に、観測値をクラス j に分類するコストを表します。コスト行列 C(i,i) の対角要素は、0 でなければなりません。前の例では、悪性腫瘍をクラス 1、良性腫瘍をクラス 2 として選択できます。この場合、コスト行列は次のように設定できます。
ここで、c > 1 は、悪性腫瘍を良性と誤診した場合のコストを表します。コストは相対値です。すべてのコストに同じ正因子を乗算しても、分類の結果に影響はありません。
クラスが 2 つだけの場合、fitcensemble では i = 1,2 および j ≠ i であるクラスについて を使用して事前確率を調整します。Pi は、fitcensemble に渡した事前確率または学習データのクラス頻度から計算された事前確率です。 は、調整された事前確率です。fitcensemble は、弱学習器の学習に調整後の確率を使用し、コスト行列は使用しません。つまり、コスト行列の操作は事前確率の操作と等価です。
3 つ以上のクラスを使用する場合も、fitcensemble は入力コストを調整済み事前確率に変換します。この変換はさらに複雑です。まず、fitcensemble は、Zhou と Liu の[1]で説明されている行列方程式を解こうとします。解を求めるのに失敗した場合は、fitcensemble は Breiman など[2]によって説明されている "平均コスト" を適用します。詳細については、Zadrozny、Langford および Abe [3]を参照してください。
不均衡な分類コストによるアンサンブルの学習
この例では、不均衡な分類コストを使用して分類木のアンサンブルに学習をさせる方法を示します。この例では、肝炎患者に関するデータを使用して、疾病によって生存するか、または死亡するかを確認します。データ セットの説明については、UCI Machine Learning Data Repository を参照してください。
UCI リポジトリから肝炎のデータ セットを文字配列として読み込みます。次に、textscan を使用して結果を文字ベクトルの cell 配列に変換します。変数名が格納されている文字ベクトルの cell 配列を指定します。
options = weboptions('ContentType','text'); hepatitis = textscan(webread(['http://archive.ics.uci.edu/ml/' ... 'machine-learning-databases/hepatitis/hepatitis.data'],options),... '%f%f%f%f%f%f%f%f%f%f%f%f%f%f%f%f%f%f%f%f','Delimiter',',',... 'EndOfLine','\n','TreatAsEmpty','?'); size(hepatitis)
ans = 1×2
1 20
VarNames = {'dieOrLive' 'age' 'sex' 'steroid' 'antivirals' 'fatigue' ...
'malaise' 'anorexia' 'liverBig' 'liverFirm' 'spleen' ...
'spiders' 'ascites' 'varices' 'bilirubin' 'alkPhosphate' 'sgot' ...
'albumin' 'protime' 'histology'};hepatitis は 1 行 20 列の文字ベクトルの cell 配列です。セルは応答 (liveOrDie) および 19 の異種混合予測子に対応します。
予測子が格納されている数値行列と、応答カテゴリの 'Die' および 'Live' が格納されている cell ベクトルを指定します。応答は 2 つの値を含みます。1 は患者が亡くなったことを、2 は患者が生存したことを意味します。応答カテゴリを使用して、応答に対応する文字ベクトルの cell 配列を指定します。hepatitis の最初の変数には応答が含まれます。
X = cell2mat(hepatitis(2:end));
ClassNames = {'Die' 'Live'};
Y = ClassNames(hepatitis{:,1});X は 19 個の予測子が格納されている数値行列です。Y は応答が格納されている文字ベクトルの cell 配列です。
欠損値についてデータを検査します。
figure barh(sum(isnan(X),1)/size(X,1)) h = gca; h.YTick = 1:numel(VarNames) - 1; h.YTickLabel = VarNames(2:end); ylabel('Predictor') xlabel('Fraction of missing values')
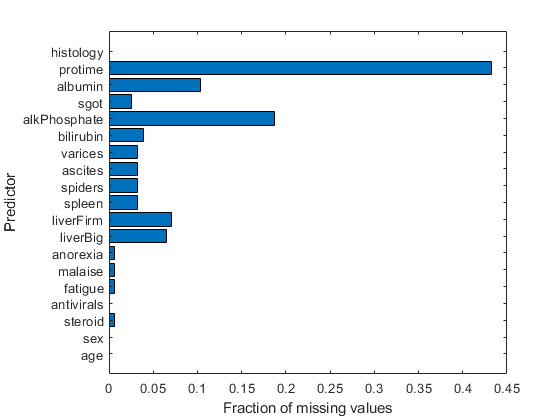
ほとんどの予測子に欠損値があり、その 1 つでは 45% 近くが欠損値となっています。そのため、代理分岐をもつ決定木を使用することによって精度を高めます。データ セットのサイズが小さいため、代理分岐を使用した場合でも学習時間はそれほど長くはなりません。
代理分岐を使用する分類木のテンプレートを作成します。
rng(0,'twister') % For reproducibility t = templateTree('surrogate','all');
データまたはデータの説明を検証して、カテゴリカル予測子を特定します。
X(1:5,:)
ans = 5×19
30.0000 2.0000 1.0000 2.0000 2.0000 2.0000 2.0000 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 1.0000 85.0000 18.0000 4.0000 NaN 1.0000
50.0000 1.0000 1.0000 2.0000 1.0000 2.0000 2.0000 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 0.9000 135.0000 42.0000 3.5000 NaN 1.0000
78.0000 1.0000 2.0000 2.0000 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 0.7000 96.0000 32.0000 4.0000 NaN 1.0000
31.0000 1.0000 NaN 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 0.7000 46.0000 52.0000 4.0000 80.0000 1.0000
34.0000 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 1.0000 NaN 200.0000 4.0000 NaN 1.0000
予測子 2 ~ 13 および予測子 19 はカテゴリカルであると考えられます。この推論は、UCI Machine Learning Data Repository のデータ セットの説明によって確認できます。
カテゴリカル変数をリストします。
catIdx = [2:13,19];
50 の学習器と GentleBoost アルゴリズムを使用して、交差検証を使用したアンサンブルを作成します。
Ensemble = fitcensemble(X,Y,'Method','GentleBoost', ... 'NumLearningCycles',50,'Learners',t,'PredictorNames',VarNames(2:end), ... 'LearnRate',0.1,'CategoricalPredictors',catIdx,'KFold',5);
混同行列を検査して、アンサンブルによって正しく予測された患者を確認します。
[yFit,sFit] = kfoldPredict(Ensemble); confusionchart(Y,yFit)
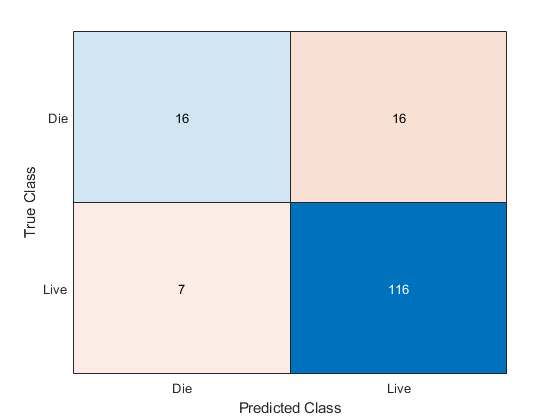
生存した 123 名の患者については、アンサンブルが 116 名の生存を正しく予測しています。しかし、肝炎で死亡した 32 名については、実際に肝炎で死亡した患者の約半数がアンサンブルにより正しく予測されただけです。
アンサンブルによる予測で発生する誤差には、次の 2 つのタイプがあります。
患者の生存を予測したにも関わらず、患者が死亡した場合
患者の死亡を予測したにも関わらず、患者が生存した場合
1 番目の誤差は 2 番目の誤差より 5 倍の悪影響をもたらすという前提があるとします。この前提を反映した新しい分類コスト行列を作成します。
cost.ClassNames = ClassNames; cost.ClassificationCosts = [0 5; 1 0];
誤分類のコストに cost を使用する新しい交差検証アンサンブルを作成して、結果の混同行列を検査します。
EnsembleCost = fitcensemble(X,Y,'Method','GentleBoost', ... 'NumLearningCycles',50,'Learners',t,'PredictorNames',VarNames(2:end), ... 'LearnRate',0.1,'CategoricalPredictors',catIdx,'KFold',5,'Cost',cost); [yFitCost,sFitCost] = kfoldPredict(EnsembleCost); confusionchart(Y,yFitCost)

予想どおり、新しいアンサンブルでは死亡する患者の分類機能が向上しています。意外なことに、新しいアンサンブルでは生存する患者の分類も向上しています。ただし、これは統計的に有意な改善ではありません。交差検証の結果は無作為であるため、この結果は単なる統計変動です。この結果から、生存する患者の分類はコストにあまり大きい影響を与えないと考えることができます。
参照
参考
fitcensemble | templateTree | kfoldLoss | kfoldPredict | confusionchart