meanfreq

周波数平均

構文

freq = meanfreq(x)

freq = meanfreq(x,fs)

freq = meanfreq(pxx,f)

freq = meanfreq(sxx,f,rbw)

freq = meanfreq(___,freqrange)

[freq,power] = meanfreq(___)

meanfreq(___)

説明

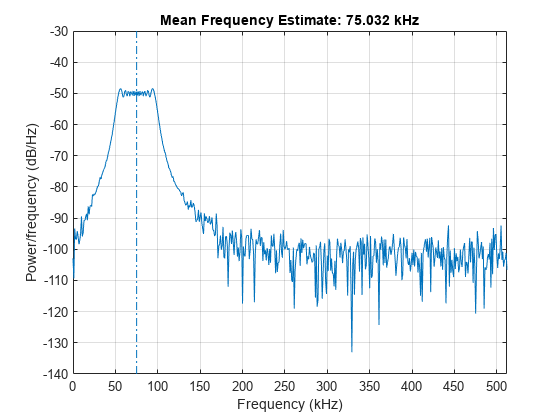
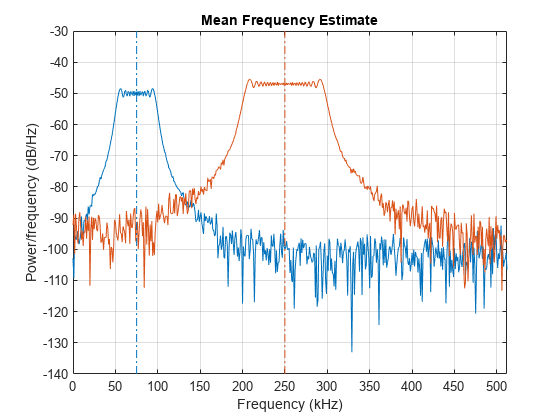
freq = meanfreq(x) は、時間領域信号 x のパワー スペクトルにおける正規化周波数の平均 freq を推定します。meanfreq は、箱型ウィンドウと x の長さに等しい DFT 点の数を持つ関数 periodogram を使用してパワー スペクトルを計算します。x が行列の場合、関数は x の各列の周波数平均を個別に計算します。

freq = meanfreq(x,fs) は、周波数平均をサンプル レート fs で推定します。

freq = meanfreq(pxx,f) は、パワー スペクトル密度 (PSD) 推定 pxx の周波数平均を返します。周波数 f は、pxx の推定値に対応します。

freq = meanfreq(sxx,f,rbw) は、分解能帯域幅 rbw でのパワー スペクトル推定 sxx の周波数平均を返します。

freq = meanfreq(___,freqrange) では、周波数平均を計算する周波数範囲を指定します。この構文には、2 番目の入力引数が fs または f である限り、前の構文の入力引数を任意に組み合わせて含めることができます。2 番目の入力が空として渡された場合は、正規化周波数と見なされます。freqrange の既定の値は、入力信号の全帯域幅です。

[freq,power] = meanfreq(___) は、スペクトルの帯域パワー power も返します。freqrange を指定した場合、power には freqrange 内の帯域パワーが含まれます。

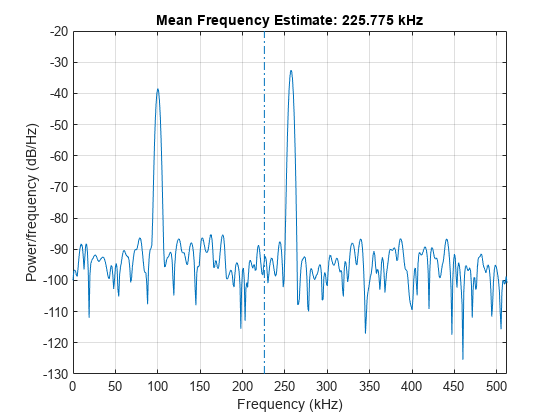
出力引数なしで meanfreq(___) を使用すると、PSD またはパワー スペクトルがプロットされて周波数平均に注釈が付けられます。

例

チャープの周波数平均

1024 kHz でサンプリングされたチャープのサンプルを 1024 個生成します。チャープの初期周波数は 50 kHz で、サンプリングの最後には 100 kHz に到達します。S/N 比が 40 dB となるホワイト ガウス ノイズを付加します。再現可能な結果が必要な場合は、乱数発生器をリセットします。

nSamp = 1024;
Fs = 1024e3;
SNR = 40;
rng default

t = (0:nSamp-1)'/Fs;

x = chirp(t,50e3,nSamp/Fs,100e3);
x = x+randn(size(x))*std(x)/db2mag(SNR);

チャープの周波数平均を推定します。パワー スペクトル密度 (PSD) をプロットして周波数平均に注釈を付けます。

meanfreq(x,Fs)

ans = 
7.5032e+04

別のチャープを生成します。初期周波数 200 kHz、最終周波数 300 kHz および最初の信号の振幅の 2 倍の振幅を指定します。ホワイト ガウス ノイズを付加します。

x2 = 2*chirp(t,200e3,nSamp/Fs,300e3);
x2 = x2+randn(size(x2))*std(x2)/db2mag(SNR);

チャープを連結して 2 チャネル信号を生成します。各チャネルの周波数平均を推定します。

y = meanfreq([x x2],Fs)

y = 1×2
105 ×

    0.7503    2.4999

2 つのチャネルの PSD をプロットし、その周波数平均に注釈を付けます。

meanfreq([x x2],Fs);

2 つのチャネルを追加して新しい信号を作成します。PSD をプロットして周波数平均に注釈を付けます。

meanfreq(x+x2,Fs)

ans = 
2.1496e+05

正弦波の周波数平均

1024 kHz でサンプリングされた 100.123 kHz の正弦波のサンプルを 1024 個生成します。S/N 比が 40 dB となるホワイト ガウス ノイズを付加します。再現可能な結果が必要な場合は、乱数発生器をリセットします。

nSamp = 1024;
Fs = 1024e3;
SNR = 40;
rng default

t = (0:nSamp-1)'/Fs;

x = sin(2*pi*t*100.123e3);
x = x + randn(size(x))*std(x)/db2mag(SNR);

periodogram を使用して、信号のパワー スペクトル密度 (PSD) を計算します。信号と同じ長さおよび形状係数 38 をもつカイザー ウィンドウを指定します。信号の周波数平均を推定し、PSD のプロット上でその推定値に注釈を付けます。

[Pxx,f] = periodogram(x,kaiser(nSamp,38),[],Fs);

meanfreq(Pxx,f);

別の正弦波を生成します。この正弦波の周波数は 257.321 kHz で、振幅は最初の正弦波の 2 倍です。ホワイト ノイズを付加します。

x2 = 2*sin(2*pi*t*257.321e3);
x2 = x2 + randn(size(x2))*std(x2)/db2mag(SNR);

正弦波を連結して 2 チャネル信号を生成します。各チャネルの PSD を推定し、結果から周波数平均を特定します。

[Pyy,f] = periodogram([x x2],kaiser(nSamp,38),[],Fs);

y = meanfreq(Pyy,f)

y = 1×2
105 ×

    1.0013    2.5732

PSD のプロット上で 2 つのチャネルの周波数平均に注釈を付けます。

meanfreq(Pyy,f);

2 つのチャネルを追加して新しい信号を作成します。PSD を推定し、周波数平均に注釈を付けます。

[Pzz,f] = periodogram(x+x2,kaiser(nSamp,38),[],Fs);

meanfreq(Pzz,f);

帯域制限された信号の周波数平均

正規化されたカットオフ周波数が $$0.25\pi$$ ラジアン/サンプルおよび $$0.45\pi$$ ラジアン/サンプルである 88 次のバンドパス FIR フィルターの周波数応答に類似した PSD をもつ信号を生成します。

d = fir1(88,[0.25 0.45]);

$$0.3\pi$$ ラジアン/サンプルと $$0.6\pi$$ ラジアン/サンプル間の信号の周波数平均を計算します。PSD をプロットして周波数平均と測定間隔に注釈を付けます。

meanfreq(d,[],[0.3 0.6]*pi);

測定間隔の周波数平均と帯域パワーを出力します。サンプル レート $$2\pi$$ の指定は、レートを設定しない場合と同じです。

[mnf,power] = meanfreq(d,2*pi,[0.3 0.6]*pi);

fprintf('Mean = %.3f*pi, power = %.1f%% of total \n', ...
    mnf/pi,power/bandpower(d)*100)

Mean = 0.373*pi, power = 75.6% of total 

正規化されたカットオフ周波数が $$0.5\pi$$ ラジアン/サンプルと $$0.8\pi$$ ラジアン/サンプルであり、最初のチャネルの 1/10 の振幅をもつ 2 番目のチャネルを追加します。

d = [d;fir1(88,[0.5 0.8])/10]';

$$0.3\pi$$ ラジアン/サンプルと $$0.9\pi$$ ラジアン/サンプル間の信号の周波数平均を計算します。PSD をプロットして各チャネルの周波数平均と測定間隔に注釈を付けます。

meanfreq(d,[],[0.3 0.9]*pi);

各チャネルの周波数平均を出力します。$$\pi$$ で除算します。

mnf = meanfreq(d,[],[0.3 0.9]*pi)/pi

mnf = 1×2

    0.3730    0.6500

入力引数

x — 入力信号

ベクトル | 行列

ベクトルまたは行列として指定される入力信号。x がベクトルの場合、単一チャネルとして取り扱われます。x が行列の場合、meanfreq は x の各列の周波数平均を個別に計算します。x は有限の値でなければなりません。

例: cos(pi/4*(0:159))+randn(1,160) は単一チャネルの行ベクトル信号です。

例: cos(pi./[4;2]*(0:159))'+randn(160,2) は 2 チャネル信号です。

データ型: single | double

fs — サンプル レート

正の実数のスカラー

サンプル レート。正の実数スカラーとして指定します。サンプル レートは単位時間あたりのサンプル数です。時間を秒単位で測定している場合、サンプル レートは Hz 単位になります。

データ型: single | double

pxx — パワー スペクトル密度

ベクトル | 行列

パワー スペクトル密度 (PSD)。ベクトルまたは行列として指定します。pxx が行列の場合、meanfreq は pxx の各列の周波数平均を個別に計算します。

パワー スペクトル密度は、デシベル単位ではなく、線形単位で表さなければなりません。デシベル値をパワー値に変換するには、db2pow を使用します。

例: [pxx,f] = periodogram(cos(pi./[4;2]*(0:159))'+randn(160,2)) は、2π Hz でサンプリングされたノイズの多い 2 チャネル正弦波のピリオドグラム PSD 推定値とそれについて計算される周波数を指定します。

データ型: single | double

f — 周波数

ベクトル

周波数。ベクトルとして指定します。

データ型: single | double

sxx — パワー スペクトル推定

ベクトル | 行列

パワー スペクトル推定。ベクトルまたは行列として指定します。sxx が行列の場合、meanfreq は sxx の各列の周波数平均を個別に計算します。

パワー スペクトルは、デシベル単位ではなく線形単位で表さなければなりません。デシベル値をパワー値に変換するには、db2pow を使用します。

例: [sxx,w] = periodogram(cos(pi./[4;2]*(0:159))'+randn(160,2),'power') では、ホワイト ガウス ノイズに組み込まれる 2 チャネルの正弦波のピリオドグラム パワー スペクトル推定と、計算に使う正規化周波数を指定します。

データ型: single | double

rbw — 分解能帯域幅

正のスカラー

分解能帯域幅。正のスカラーで指定されます。この分解能帯域幅は、2 つの値、離散フーリエ変換の周波数分解能と PSD の計算に使用されるウィンドウの等価ノイズ帯域幅の積です。

データ型: single | double

freqrange — 周波数範囲

2 要素ベクトル

周波数範囲。実数値の 2 要素ベクトルとして指定します。freqrange を指定しない場合、meanfreq は入力信号の全帯域幅を使用します。

データ型: single | double

出力引数

freq — 周波数平均

スカラー | ベクトル

周波数平均。スカラー値またはベクトルとして指定します。

• サンプル レートを指定した場合、freq の単位は fs の単位と同じになります。

• サンプル レートを指定しない場合、freq の単位はラジアン/サンプルになります。

power — 帯域パワー

スカラー | ベクトル

帯域パワー。スカラーまたはベクトルで返されます。

アルゴリズム

平均周波数を求めるために、meanfreq は箱型ウィンドウを使用してピリオドグラム パワー スペクトル推定を計算します。

サンプル レート fs の信号 x から、次の 3 つの方法で同じ平均周波数値 mFrq を求めることができます。

信号から直接	mFrq = meanfreq(x,fs)
信号のピリオドグラムから	[P,F] = periodogram(x,[],[],fs); mFrq = meanfreq(P,F)
信号のパワー スペクトル推定値 (ウェルチの PSD) から	[P,F] = pwelch(x,rectwin(length(x)),[],[],fs); mFrq = meanfreq(P,F)

メモ

meanfreq は、入力信号を時間領域から周波数領域に変換するために中間表現を使用するため、返される平均周波数は信号変換方法、DFT 点の数、およびウィンドウ サイズに応じて異なる場合があります。

参照

[1] Phinyomark, Angkoon, Sirinee Thongpanja, Huosheng Hu, Pornchai Phukpattaranont, and Chusak Limsakul. "The Usefulness of Mean and Median Frequencies in Electromyography Analysis." In Computational Intelligence in Electromyography Analysis – A Perspective on Current Applications and Future Challenges, edited by Ganesh R. Naik. London: IntechOpen, 2012. https://doi.org/10.5772/50639.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

使用上の注意および制限:

• 出力引数のない構文はサポートされません。

詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2015a で導入

R2022b: gpuArray オブジェクトの使用

関数 meanfreq は gpuArray オブジェクトをサポートしています。この機能を使用するには、Parallel Computing Toolbox™ が必要です。

参考

findpeaks | medfreq | periodogram | plomb | pwelch