firpm
Parks-McClellan 最適 FIR フィルターの設計
構文
説明
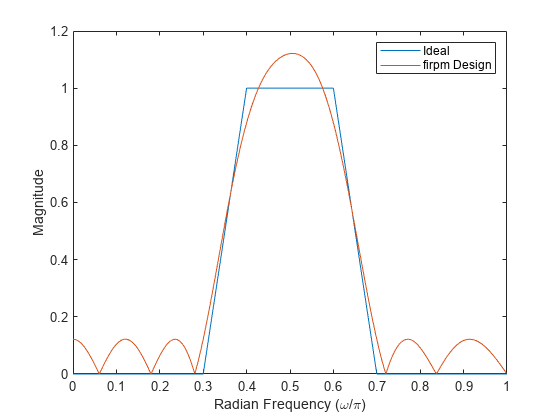
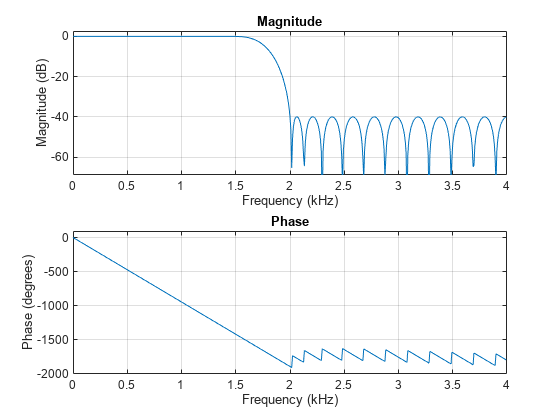
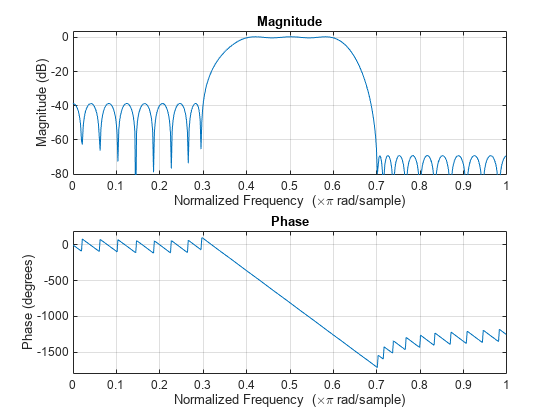
例
入力引数
出力引数
詳細
ヒント
フィルター設計が収束しない場合、フィルター設計が正しくない可能性があります。周波数応答を調べて設計を検証してください。
フィルター設計が収束せず、生成されたフィルター設計が正しくない場合は、以下のうち 1 つまたは複数を試してください。
フィルター次数を大きくします。
阻止帯域の減衰を小さくするか遷移領域を拡大する (あるいはその両方を行う) ことで、フィルターの設計を緩和します。
アルゴリズム
firpm では、Parks-McClellan アルゴリズム [2] を使用して、線形位相 FIR フィルターが設計されます。Parks-McClellan アルゴリズムは、Remez 交換アルゴリズムとチェビシェフ近似理論を使用し、希望する周波数応答と実際の周波数応答が最も近づくようにフィルターを設計します。フィルターは、希望周波数応答と実際の周波数応答間の最大誤差が最小化されているという点で、最適化されているといえます。この方法で設計されたフィルターは、周波数応答で等リップル動作を示すため、等リップル フィルターと呼ばれる場合もあります。firpm は、この等リップル特性のため、インパルス応答の最初と最後に不連続性を示します。
これらは、I 型 (次数 n が奇数) と II 型 (n が偶数) の線形位相フィルターになります。ベクトル f と a では、フィルターの周波数-振幅特性が指定されます。
fは、0 ~ 1 の範囲で指定される周波数点のベクトルで、1 はナイキスト周波数に対応します。周波数は増加する順でなければなりません。aは、fで指定した点で目的の振幅を含むベクトルです。k が奇数の場合、(f(k), f(k+1)) 両点間の周波数における目的の振幅関数は、点 (f(k), a(k)) と点 (f(k+1), a(k+1)) を結ぶライン セグメントです。
k が偶数の場合、(f(k), f(k+1)) 両点間の周波数における目的の振幅関数は指定されません。これらは遷移領域、つまり "don't care" 領域です。
fとaは、同じ長さです。この長さは、偶数でなければなりません。
目的の振幅応答を定義する際のベクトル f と a の関係は、以下のようになります。

firpm では、偶数の対称性と、ナイキスト周波数で非ゼロの通過帯域をもつ構成に対し、常に偶数のフィルター次数が使用されます。これは、偶数のフィルター次数が偶数の対称性と奇数の次数を示すインパルス応答に対し、ナイキスト周波数での周波数応答が必ず 0 になるからです。n に奇数の値を指定した場合、firpm によりこの値に 1 が加算されます。
firpm では、I 型、II 型、III 型、および IV 型の線形位相フィルターが設計されます。I 型および II 型は、それぞれ偶数 n および奇数 n の既定フィルターです。III 型 (n が偶数) および IV 型 (n が奇数) は、ftype 引数を使用して、それぞれ 'hilbert' または 'differentiator' で指定されます。異なるタイプのフィルターは、周波数応答に対して異なる対称性および制約をもちます (詳細については、[3]を参照してください。)
| 線形位相フィルター タイプ | フィルター次数 | 係数の対称性 | f = 0 での応答 H(f) | f = 1 (ナイキスト) での応答 H(f) |
|---|---|---|---|---|
I 型 | 偶数 | 偶数: | 制約なし | 制約なし |
II 型 | 奇数 | 偶数: | 制約なし | H(1)
|
III 型 | 偶数 | 奇数: | H(0) | H(1) |
| IV 型 | 奇数 | 奇数: | H(0) | 制約なし |
firpm を使用して、希望する周波数応答を定義する関数を作成することもできます。詳細については、ユーザー定義の周波数応答関数を参照してください。
参照
[1] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Selected Papers in Digital Signal Processing. Vol. II. New York: IEEE Press, 1976.
[2] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979, algorithm 5.1.
[3] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999, p. 486.
[4] Parks, Thomas W., and C. Sidney Burrus. Digital Filter Design. New York: John Wiley & Sons, 1987, p. 83.
[5] Rabiner, Lawrence R., James H. McClellan, and Thomas W. Parks. "FIR Digital Filter Design Techniques Using Weighted Chebyshev Approximation." Proceedings of the IEEE®. Vol. 63, Number 4, 1975, pp. 595–610.
拡張機能
バージョン履歴
R2006a より前に導入