issatisfied
構文
説明
例
いくつかの線形制約と非線形制約を含む最適化問題を作成します。
x = optimvar("x"); y = optimvar("y"); obj = (10*(y - x^2))^2 + (1 - x)^2; cons1 = x^2 + y^2 <= 1; cons2 = x + y >= 0; cons3 = y <= sin(x); cons4 = 2*x + 3*y <= 2.5; prob = optimproblem(Objective=obj); prob.Constraints.cons1 = cons1; prob.Constraints.cons2 = cons2; prob.Constraints.cons3 = cons3; prob.Constraints.cons4 = cons4;
100 個のテスト ポイントをランダムに作成します。
rng default % For reproducibility xvals = randn(1,100); yvals = randn(1,100);
点を問題の OptimizationValues オブジェクトに変換し、それらの点の中からすべての制約を満たす点を特定します。
vals = optimvalues(prob,x=xvals,y=yvals); allsat = issatisfied(prob,vals);
実行可能な (満たされている) 点を緑の円、実行不可能な点を赤の x 印でプロットします。
xsat = xvals(allsat); ysat = yvals(allsat); xnosat = xvals(~allsat); ynosat = yvals(~allsat); plot(xsat,ysat,"go",xnosat,ynosat,"rx")
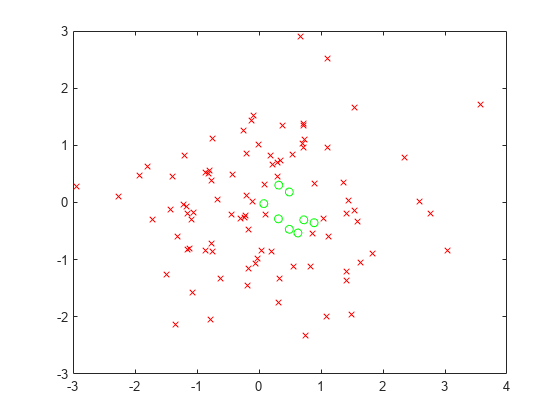
2 つの最適化変数と 3 行 2 列の不等式制約の配列を作成します。
x = optimvar("x"); y = optimvar("y"); cons = optimconstr(3,2); cons(1,1) = x^2 + y^2/4 <= 2; cons(1,2) = 3*x + y <= 4; cons(2,1) = -x - y^3 <= -3; cons(2,2) = 2*x^2 + x*y + 4*y^2 <= 6; cons(3,1) = 2*x + 4*x*y + y^2 <= 5; cons(3,2) = (4 + x*y)^2 <= 24;
点 x = 1/2、y = -1/2 ですべての制約が満たされているかどうかをチェックします。
pt.x = 1/2; pt.y = -1/2; allsat = issatisfied(cons,pt)
allsat = logical
0
すべての制約は満たされていません。どれが満たされているかを調べます。
[allsat,sat] = issatisfied(cons,pt)
allsat = logical
0
sat = 3×2 logical array
1 1
0 1
1 1
constraint(2,1) 以外はすべて満たされています。
いくつかの線形制約と非線形制約を含む最適化問題を作成します。
x = optimvar("x"); y = optimvar("y"); obj = (10*(y - x^2))^2 + (1 - x)^2; cons1 = x^2 + y^2 <= 1; cons2 = x + y >= 0; cons3 = y <= sin(x); cons4 = 2*x + 3*y <= 2.5; prob = optimproblem(Objective=obj); prob.Constraints.cons1 = cons1; prob.Constraints.cons2 = cons2; prob.Constraints.cons3 = cons3; prob.Constraints.cons4 = cons4;
100 個のテスト ポイントをランダムに作成します。
rng default % For reproducibility xvals = randn(1,100); yvals = randn(1,100);
点を問題の OptimizationValues オブジェクトに変換し、それらの点の中からすべての制約を満たす点を特定します。
vals = optimvalues(prob,x=xvals,y=yvals); allsat = issatisfied(prob,vals);
実行可能な (満たされている) 点を緑の円、実行不可能な点を赤の x 印でプロットします。
xsat = xvals(allsat); ysat = yvals(allsat); xnosat = xvals(~allsat); ynosat = yvals(~allsat); plot(xsat,ysat,"go",xnosat,ynosat,"rx")
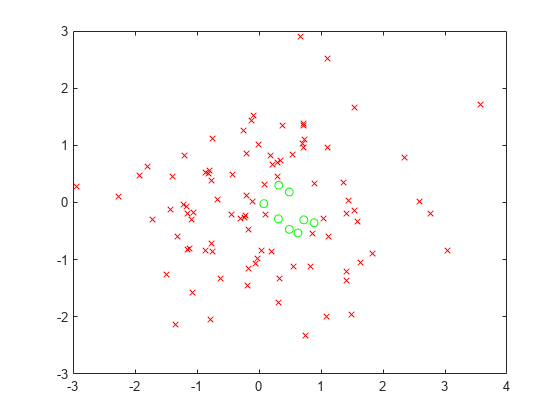
既定の 1e-6 ではなく、許容誤差 1 に関して実行可能な点を特定します。
tol = 1; allsat1 = issatisfied(prob,vals,tol);
実行可能な (満たされている) 点を緑の円、実行不可能な点を赤の x 印でプロットします。
xsat1 = xvals(allsat1); ysat1 = yvals(allsat1); xnosat1 = xvals(~allsat1); ynosat1 = yvals(~allsat1); plot(xsat1,ysat1,"go",xnosat1,ynosat1,"rx")
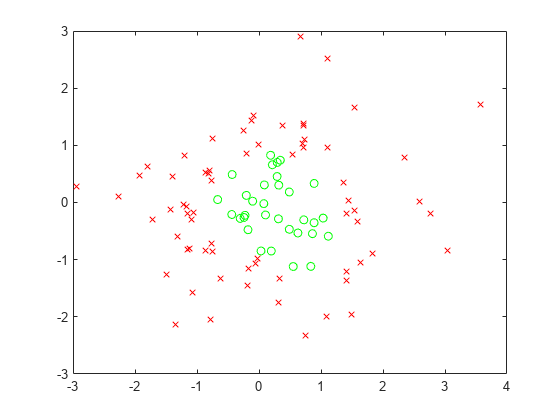
制約満足度の定義を緩くすると、より多くの点が実行可能になります。
いくつかの線形制約と非線形制約を含む最適化問題を作成します。
x = optimvar("x"); y = optimvar("y"); obj = (10*(y - x^2))^2 + (1 - x)^2; cons1 = x^2 + y^2 <= 1; cons2 = x + y >= 0; cons3 = y <= sin(x); cons4 = 2*x + 3*y <= 2.5; prob = optimproblem(Objective=obj); prob.Constraints.cons1 = cons1; prob.Constraints.cons2 = cons2; prob.Constraints.cons3 = cons3; prob.Constraints.cons4 = cons4;
100 個のテスト ポイントをランダムに作成します。
rng default % For reproducibility xvals = randn(1,100); yvals = randn(1,100);
点を問題の OptimizationValues オブジェクトに変換します。
vals = optimvalues(prob,x=xvals,y=yvals);
点で制約を評価します。issatisfied は、すべての制約満足度をすべてのテスト ポイントで同時に評価します。
[~,sat] = issatisfied(prob,vals);
最初の制約について、実行可能な (満たされている) 点を緑の円、実行不可能な点を赤の x 印でプロットします。
x1sat = xvals(sat.cons1); y1sat = yvals(sat.cons1); x1nosat = xvals(~sat.cons1); y1nosat = yvals(~sat.cons1); plot(x1sat,y1sat,"go",x1nosat,y1nosat,"rx") title("Constraint 1 Satisfaction")
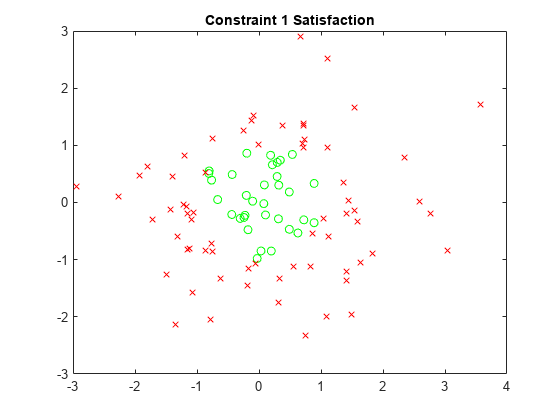
この処理を他の 3 つの制約について繰り返します。
x2sat = xvals(sat.cons2); y2sat = yvals(sat.cons2); x2nosat = xvals(~sat.cons2); y2nosat = yvals(~sat.cons2); plot(x2sat,y2sat,"go",x2nosat,y2nosat,"rx") title("Constraint 2 Satisfaction")
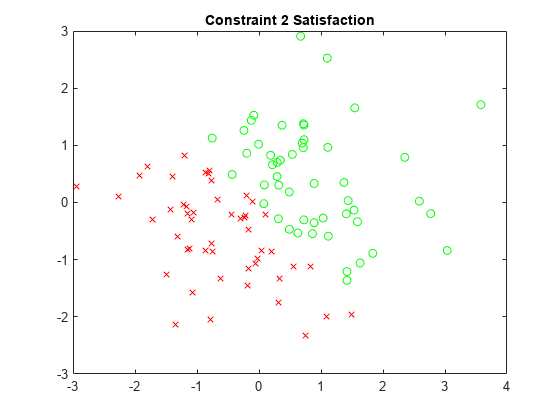
x3sat = xvals(sat.cons3); y3sat = yvals(sat.cons3); x3nosat = xvals(~sat.cons3); y3nosat = yvals(~sat.cons3); plot(x3sat,y3sat,"go",x3nosat,y3nosat,"rx") title("Constraint 3 Satisfaction")
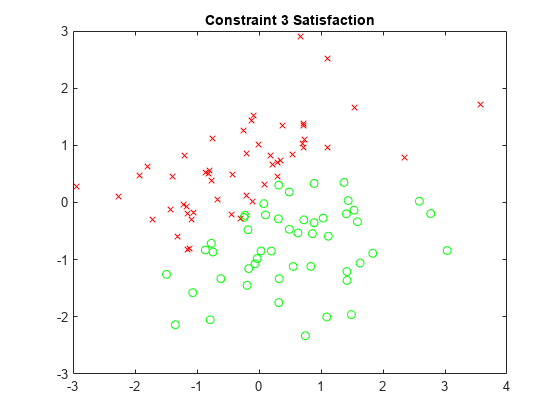
x4sat = xvals(sat.cons4); y4sat = yvals(sat.cons4); x4nosat = xvals(~sat.cons4); y4nosat = yvals(~sat.cons4); plot(x4sat,y4sat,"go",x4nosat,y4nosat,"rx") title("Constraint 4 Satisfaction")
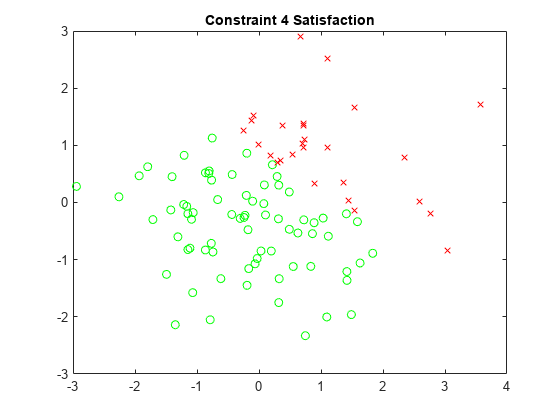
プロットは、制約ごとに異なる満足度の領域を示します。
2 つの最適化変数で一連の方程式を作成します。
x = optimvar("x"); y = optimvar("y"); prob = eqnproblem; prob.Equations.eq1 = x^2 + y^2/4 == 2; prob.Equations.eq2 = x^2/4 + 2*y^2 == 2;
から始めて連立方程式を解きます。
x0.x = 1; x0.y = 1/2; sol = solve(prob,x0)
Solving problem using fsolve. Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
sol = struct with fields:
x: 1.3440
y: 0.8799
点 x0 と sol で方程式を評価します。
vars = optimvalues(prob,x=[x0.x sol.x],y=[x0.y sol.y]); vals = evaluate(prob,vars)
vals =
1×2 OptimizationValues vector with properties:
Variables properties:
x: [1 1.3440]
y: [0.5000 0.8799]
Equation properties:
eq1: [0.9375 8.4322e-10]
eq2: [1.2500 6.7431e-09]
最初の点 x0 は、eq1 と eq2 の両方の方程式の値が非ゼロです。2 つ目の点 sol は、解に期待されるとおり、それらの方程式の値がほぼゼロになります。
issatisfied を使用して方程式の満足度を調べます。
[satisfied details] = issatisfied(prob,vars)
satisfied = 1×2 logical array
0 1
details =
1×2 OptimizationValues vector with properties:
Variables properties:
x: [1 1.3440]
y: [0.5000 0.8799]
Equation properties:
eq1: [0 1]
eq2: [0 1]
最初の点 x0 は解ではなく、その点の satisfied は 0 です。2 つ目の点 sol は解であり、その点の satisfied は 1 です。方程式のプロパティは、最初の点ではどちらの方程式も満たされず、2 つ目の点では両方が満たされることを示しています。
