fill3

塗りつぶされた 3 次元パッチの作成

• 

構文

fill3(X,Y,Z,C)

fill3(X1,Y1,Z1,C1,...,Xn,Yn,Zn,Cn)

fill3(___,Name,Value)

fill3(ax,___)

p = fill3(___)

説明

fill3(X,Y,Z,C) は、塗りつぶされた多角形領域を 3 次元座標軸に Patch オブジェクトとしてプロットします。頂点の位置 (x,y,z) は X、Y、および Z で指定します。

• 1 つの領域をプロットするには、X、Y、および Z をベクトルとして指定します。

• 複数の領域をプロットするには、X、Y、および Z を、各列が 1 つの多角形に対応する行列として指定します。

C は領域の塗りつぶし色を決定します。

fill3(X1,Y1,Z1,C1,...,Xn,Yn,Zn,Cn) は、複数の塗りつぶされた多角形領域を同じ 3 次元座標軸上にプロットします。

fill3(___,Name,Value) は、1 つ以上の名前と値の引数を使用してプロパティを設定し、Patch オブジェクトを変更します。パッチは、前述の構文にある任意の入力引数の組み合わせを使用して指定できます。たとえば、fill3(X,Y,Z,C,'LineWidth',2) は、すべてのパッチの周囲に 2 ポイントの境界線を指定します。プロパティの一覧については、Patch のプロパティを参照してください。

fill3(ax,___) は、現在の座標軸 (gca) ではなく、ax で指定した座標軸に多角形領域をプロットします。

p = fill3(___) は、Patch オブジェクト、または Patch オブジェクトのベクトルを返します。領域をプロットした後にプロパティのクエリと変更を行うには、p を使用します。プロパティの完全な一覧については、Patch のプロパティを参照してください。

例

3 次元座標軸での塗りつぶされた三角形の作成

ベクトル x、y、および z を三角形の頂点の (x,y,z) 座標として指定します。次に、指定した塗りつぶし色 (赤) でその三角形をプロットします。

x = [0 0 0];
y = [0 2 1];
z = [0 0 2];
fill3(x,y,z,'r')

カスタムの塗りつぶし色の指定

ベクトル x1、y1、z1 と x2、y2、z2 を 2 つの四角形の頂点の (x,y,z) 座標として定義します。各四角形の色を RGB 3 成分として指定します。各値では、色の赤、緑、青成分の強度を指定します。両方の四角形を単一の fill3 呼び出しでプロットします。

x1 = [0 0 1 1];
y1 = [3 3 2 2];
z1 = [0 3 2 1];
c1 = [0 0.447 0.741];
x2 = [2 2 3 3];
y2 = [1 1 0 0];
z2 = [1 2 3 0];
c2 = [0.850 0.325 0.098];
fill3(x1,y1,z1,c1,x2,y2,z2,c2)

頂点からの塗りつぶし色の内挿

行列 x、y、および z を 3 つの隣接する正方形の頂点の座標として指定します。c を x、y、および z と同じ次元の行列として指定します。c の各値は、対応する頂点のカラーマップ インデックスを指定します。関数 fill3 は、頂点の色から各正方形の塗りつぶし色を内挿します。

x = [0 0 0; 0 0 2; 0 2 2; 0 2 0];
y = [2 0 2; 0 0 2; 0 0 0; 2 0 0];
z = [2 0 2; 2 2 2; 0 2 2; 0 0 2];
c = [2 2 2; 3 3 0; 2 2 2; 0 0 3];
fill3(x,y,z,c)

作成後のパッチの変更

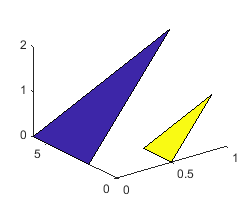
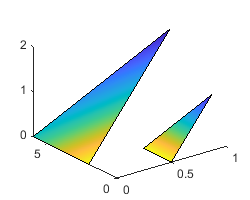
カラーマップ インデックスのベクトル c によって指定された塗りつぶし色で 2 つの三角形をプロットします。返された 2 つのパッチをベクトル p に保存します。

x = [0 1; 1.5 2.5; 3 4];
y = [4 4; 2.5 2.5; 1 1];
z = [0 0; 2 2; 0 0];
c = [1 0];
p = fill3(x,y,z,c);

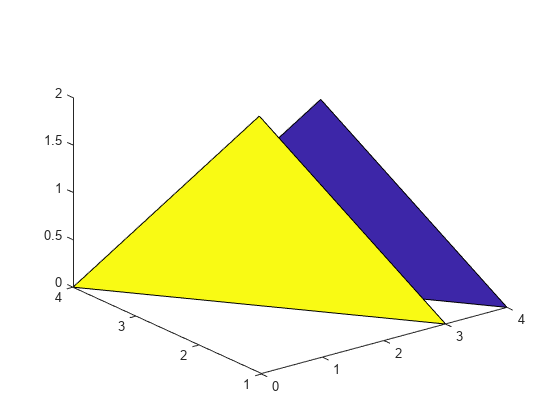
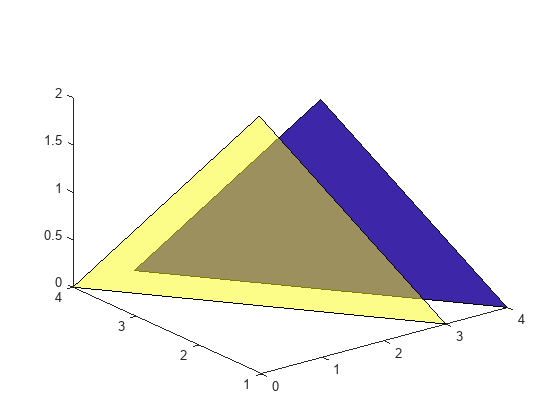
p を使用して最初の三角形を変更します。p の最初の要素の FaceAlpha プロパティを変更して、最初の三角形を透明にします。

p(1).FaceAlpha = 0.5;

入力引数

X — パッチの頂点の x 座標

ベクトル | 行列

パッチの頂点の x 座標。ベクトルまたは行列として指定します。

パッチ数	説明	例
1 つのパッチ	X、Y、および Z を同じ長さのベクトルとして指定します。これらのベクトルは任意の向きにできます。	1 つの三角形パッチをプロットします。 X = [0 0 4]; Y = [2 4 2]; Z = [1 1 1]; C = 1; fill3(X,Y,Z,C)
複数のパッチ (共有している X、Y、または Z)	共有している座標をベクトルとして指定します。その他の座標は行列として指定します。ベクトルの長さは行列の次元の 1 つの長さと一致していなければなりません。行列が正方の場合、MATLAB® は行列の列をベクトルに対してプロットします。	共有している x 座標と z 座標を使用して 2 つの三角形パッチをプロットします。 X = [0 0 4]; Y = [0 -0; 2 -2; 0 0]; Z = [0 0 0]; C = [0 1]; fill3(X,Y,Z,C)
複数のパッチ (X、Y、および Z は一意)	X、Y、および Z を、同じサイズの行列として指定します。MATLAB はこれらの行列の対応する列をプロットします。	一意の x 座標、y 座標、および z 座標を使用して 2 つの三角形パッチをプロットします。 X = [0 5; 0 5; 4 9]; Y = [2 0; 4 2; 2 0]; Z = [0 1; 2 3; 1 2]; C = [0 1]; fill3(X,Y,Z,C)

データで閉じた領域が定義されていない場合、fill3 によって領域が閉じられます。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration

Y — パッチの頂点の y 座標

ベクトル | 行列

パッチの頂点の y 座標。ベクトルまたは行列として指定します。

パッチ数	説明	例
1 つのパッチ	X、Y、および Z を同じ長さのベクトルとして指定します。これらのベクトルは任意の向きにできます。	1 つの三角形パッチをプロットします。 X = [0 0 4]; Y = [2 4 2]; Z = [1 1 1]; C = 1; fill3(X,Y,Z,C)
複数のパッチ (共有している X、Y、または Z)	共有している座標をベクトルとして指定します。その他の座標は行列として指定します。ベクトルの長さは行列の次元の 1 つの長さと一致していなければなりません。行列が正方の場合、MATLAB は行列の列をベクトルに対してプロットします。	共有している x 座標と z 座標を使用して 2 つの三角形パッチをプロットします。 X = [0 0 4]; Y = [0 -0; 2 -2; 0 0]; Z = [0 0 0]; C = [0 1]; fill3(X,Y,Z,C)
複数のパッチ (X、Y、および Z は一意)	X、Y、および Z を、同じサイズの行列として指定します。MATLAB はこれらの行列の対応する列をプロットします。	一意の x 座標、y 座標、および z 座標を使用して 2 つの三角形パッチをプロットします。 X = [0 5; 0 5; 4 9]; Y = [2 0; 4 2; 2 0]; Z = [0 1; 2 3; 1 2]; C = [0 1]; fill3(X,Y,Z,C)

データで閉じた領域が定義されていない場合、fill3 によって領域が閉じられます。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration

Z — パッチの頂点の z 座標

ベクトル | 行列

パッチの頂点の z 座標。ベクトルまたは行列として指定します。

パッチ数	説明	例
1 つのパッチ	X、Y、および Z を同じ長さのベクトルとして指定します。これらのベクトルは任意の向きにできます。	1 つの三角形パッチをプロットします。 X = [0 0 4]; Y = [2 4 2]; Z = [1 1 1]; C = 1; fill3(X,Y,Z,C)
複数のパッチ (共有している X、Y、または Z)	共有している座標をベクトルとして指定します。その他の座標は行列として指定します。ベクトルの長さは行列の次元の 1 つの長さと一致していなければなりません。行列が正方の場合、MATLAB は行列の列をベクトルに対してプロットします。	共有している x 座標と z 座標を使用して 2 つの三角形パッチをプロットします。 X = [0 0 4]; Y = [0 -0; 2 -2; 0 0]; Z = [0 0 0]; C = [0 1]; fill3(X,Y,Z,C)
複数のパッチ (X、Y、および Z は一意)	X、Y、および Z を、同じサイズの行列として指定します。MATLAB はこれらの行列の対応する列をプロットします。	一意の x 座標、y 座標、および z 座標を使用して 2 つの三角形パッチをプロットします。 X = [0 5; 0 5; 4 9]; Y = [2 0; 4 2; 2 0]; Z = [0 1; 2 3; 1 2]; C = [0 1]; fill3(X,Y,Z,C)

データで閉じた領域が定義されていない場合、fill3 によって領域が閉じられます。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration

C — パッチの色

色名 | RGB 3 成分 | カラーマップ インデックスのベクトル | カラーマップ インデックスの行列 | ...

パッチの色。色名、RGB 3 成分、カラーマップ インデックスのベクトル、またはカラーマップ インデックスの行列として指定します。

• 色名 — 'red' のような色名、または 'r' のような省略名。

• RGB 3 成分 — 色の赤、緑、青成分の強度を指定する 3 要素の行ベクトル。強度値は [0,1] の範囲でなければなりません。たとえば [0.4 0.6 0.7] のようになります。RGB 3 成分は、カスタム色を作成するのに役立ちます。

• カラーマップ インデックスのベクトル — 領域ごとに 1 つの要素をもつ、数値のベクトル。

• カラーマップ インデックスの行列 — X、Y、および Z と同じ次元をもつ、数値の行列。

色を指定する方法は、配色や、プロットする多角形領域が 1 つであるか複数であるかによって異なります。次の表では、最も一般的な状況について説明します。

配色	色の指定方法	例
すべての領域に単色を適用	次の表のいずれかの色名または省略名を指定するか、1 つの RGB 3 成分を指定します。	行列 x、y、z を作成します。次に、赤で塗りつぶされた領域をプロットします。 x = [0.5 0; 0.5 0; 1 1]; y = [0 2; 2 6; 1 4]; z = [0 0; 0 0; 1 2]; fill3(x,y,z,'r')
領域ごとに 1 つの色	カラーマップ インデックスの n 行 1 列または 1 行 n 列のベクトルを指定します。ここで、n は多角形領域の数です。	行列 x、y、z、およびベクトル c を作成します。次に、指定したカラーマップの色で塗りつぶされた領域をプロットします。 x = [0.5 0; 0.5 0; 1 1]; y = [0 2; 2 6; 1 4]; z = [0 0; 0 0; 1 2]; c = [1 0]; fill3(x,y,z,c)
面の色の内挿	m 行 n 列のカラーマップ インデックスの行列を指定します。ここで、[m,n] = size(X) です。頂点ごとに 1 つの色を指定します。	行列 x、y、z、および c を作成します。次に、頂点の色 c から内挿された塗りつぶし色で塗りつぶされた領域をプロットします。 x = [0.5 0; 0.5 0; 1 1]; y = [0 2; 2 6; 1 4]; z = [0 0; 0 0; 1 2]; c = [1 1; 1 0.5; 0 0]; fill3(x,y,z,c)

一般的な色の色名と RGB 3 成分

色名	省略名	RGB 3 成分	16 進数カラー コード	外観
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"

次の表に、ライト テーマとダーク テーマでのプロットの既定のカラー パレットを示します。

パレット	パレットの色
"gem" — ライト テーマの既定値 R2025a より前: ほとんどのプロットで、これらの色が既定で使用されます。
"glow" — ダーク テーマの既定値

orderedcolors 関数と rgb2hex 関数を使用すると、これらのパレットの RGB 3 成分および 16 進数カラー コードを取得できます。たとえば、"gem" パレットの RGB 3 成分を取得し、16 進数カラー コードに変換します。

RGB = orderedcolors("gem");
H = rgb2hex(RGB);

R2023b より前: RGB = get(groot,"FactoryAxesColorOrder") を使用して、RGB 3 成分を取得します。

R2024a より前: H = compose("#%02X%02X%02X",round(RGB*255)) を使用して、16 進数カラー コードを取得します。

ax — プロットする座標軸

Axes オブジェクト | PolarAxes オブジェクト

プロットする座標軸。Axes オブジェクトまたは PolarAxes オブジェクトとして指定します。座標軸を指定しない場合、fill3 は現在の座標軸にプロットするか Axes オブジェクト (直交座標軸) を作成します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: fill3(x,y,z,c,'FaceAlpha',.5,'LineStyle',':') は、点線のエッジをもつ半透明の多角形を作成します。

メモ

ここでは、パッチ プロパティの一部だけを紹介しています。完全な一覧については、Patch のプロパティ を参照してください。

FaceColor — 面の色

'interp' | 'flat' | RGB 3 成分 | 16 進数カラー コード | 'r' | 'g' | 'b' | ...

面の色。'interp'、'flat' RGB 3 成分、16 進数カラー コード、色名、または省略名として指定します。

各面に異なる色を作成するには、面ごとに 1 つの色または頂点ごとに 1 つの色を含む配列として CData または FaceVertexCData プロパティを指定します。色は面ごとに周囲の頂点の色から内挿することも、一様にすることもできます。内挿された色の場合、このプロパティを 'interp' として指定します。一様な色の場合、このプロパティを 'flat' として指定します。頂点ごとに 'flat' と異なる色を指定すると、指定する最初の頂点の色によって面の色が決まります。

すべての面に単色を指定するには、このプロパティを RGB 3 成分、16 進数カラー コード、色名、または省略名として指定します。

• RGB 3 成分は、色の赤、緑、青成分の強度を指定する 3 成分の行ベクトルです。強度値は [0,1] の範囲でなければなりません。たとえば [0.4 0.6 0.7] のようになります。

• 16 進数カラー コードは、ハッシュ記号 (#) で始まり、3 桁または 6 桁の 0 から F までの範囲の 16 進数が続く文字ベクトルまたは string スカラーです。この値は大文字と小文字を区別しません。したがって、カラー コード '#FF8800'、'#ff8800'、'#F80'、および '#f80' は等価です。

色名	省略名	RGB 3 成分	16 進数カラー コード	外観
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"
"none"	該当なし	該当なし	該当なし	色なし

次の表に、ライト テーマとダーク テーマでのプロットの既定のカラー パレットを示します。

パレット	パレットの色
"gem" — ライト テーマの既定値 R2025a より前: ほとんどのプロットで、これらの色が既定で使用されます。
"glow" — ダーク テーマの既定値

orderedcolors 関数と rgb2hex 関数を使用すると、これらのパレットの RGB 3 成分および 16 進数カラー コードを取得できます。たとえば、"gem" パレットの RGB 3 成分を取得し、16 進数カラー コードに変換します。

RGB = orderedcolors("gem");
H = rgb2hex(RGB);

R2023b より前: RGB = get(groot,"FactoryAxesColorOrder") を使用して、RGB 3 成分を取得します。

R2024a より前: H = compose("#%02X%02X%02X",round(RGB*255)) を使用して、16 進数カラー コードを取得します。

FaceAlpha — 面の透明度

1 (既定値) | 範囲 [0,1] のスカラー | 'flat' | 'interp'

面の透明度。次の値のいずれかとして指定します。

• 範囲 [0,1] のスカラー — すべての面に一様な透明度を使用します。値 1 は完全に不透明で、値 0 は完全に透明です。このオプションは FaceVertexAlphaData プロパティの透明度値を使用しません。

• 'flat' — FaceVertexAlphaData プロパティの値に基づいて面ごとに異なる透明度を使用します。まず、FaceVertexAlphaData プロパティを、面または頂点ごとに 1 つの透明度値を含むベクトルとして指定しなければなりません。面全体の透明度は、最初の頂点の透明度値によって決まります。

• 'interp' — FaceVertexAlphaData プロパティの値に基づいて面ごとに内挿された透明度を使用します。まず、FaceVertexAlphaData プロパティを、頂点ごとに 1 つの透明度値を含むベクトルとして指定しなければなりません。頂点の値を内挿することにより、各面に異なる透明度が使用されます。

EdgeColor — エッジの色

'none' | 'flat' | 'interp' | RGB 3 成分 | 16 進数カラー コード | 'r' | 'g' | 'b' | ...

エッジの色。次の表のいずれかの値として指定します。エッジの既定色は黒で、[0 0 0] の値で指定されます。複数の多角形で共有されるエッジの場合、その表示色は最初に描画された多角形によって決まります。

値	説明	結果
RGB 3 成分、16 進数カラー コード、色名	すべてのエッジに 1 つの色を使用します。詳細については、次の表を参照してください。
'flat'	エッジごとに異なる色を使用します。エッジの色を設定するには、その前の頂点の色を指定します。まず、頂点ごとに 1 つの色を含む配列として CData または FaceVertexCData を指定しなければなりません。エッジの色は、頂点を指定した順序によって決まります。
'interp'	内挿されたエッジの色。まず、頂点ごとに 1 つの色を含む配列として CData または FaceVertexCData を指定しなければなりません。エッジの色を指定するには、2 つの境界頂点の値を線形内挿します。
'none'	エッジは表示されません。	エッジは表示されません。

RGB 3 成分および 16 進数カラー コードは、カスタム色を指定するのに役立ちます。

• RGB 3 成分は、色の赤、緑、青成分の強度を指定する 3 成分の行ベクトルです。強度値は [0,1] の範囲でなければなりません。たとえば [0.4 0.6 0.7] のようになります。

• 16 進数カラー コードは、ハッシュ記号 (#) で始まり、3 桁または 6 桁の 0 から F までの範囲の 16 進数が続く文字ベクトルまたは string スカラーです。この値は大文字と小文字を区別しません。したがって、カラー コード "#FF8800"、"#ff8800"、"#F80"、および "#f80" は等価です。

あるいは、名前を使用して一部の一般的な色を指定できます。次の表に、名前の付いた色オプション、等価の RGB 3 成分、および 16 進数カラー コードを示します。

色名	省略名	RGB 3 成分	16 進数カラー コード	外観
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"

次の表に、ライト テーマとダーク テーマでのプロットの既定のカラー パレットを示します。

パレット	パレットの色
"gem" — ライト テーマの既定値 R2025a より前: ほとんどのプロットで、これらの色が既定で使用されます。
"glow" — ダーク テーマの既定値

orderedcolors 関数と rgb2hex 関数を使用すると、これらのパレットの RGB 3 成分および 16 進数カラー コードを取得できます。たとえば、"gem" パレットの RGB 3 成分を取得し、16 進数カラー コードに変換します。

RGB = orderedcolors("gem");
H = rgb2hex(RGB);

R2023b より前: RGB = get(groot,"FactoryAxesColorOrder") を使用して、RGB 3 成分を取得します。

R2024a より前: H = compose("#%02X%02X%02X",round(RGB*255)) を使用して、16 進数カラー コードを取得します。

LineStyle — ライン スタイル

"-" (既定値) | "--" | ":" | "-." | "none"

ライン スタイル。次の表にリストされたオプションのいずれかとして指定します。

ライン スタイル	説明	結果として得られる線
"-"	実線
"--"	破線
":"	点線
"-."	一点鎖線
"none"	ラインなし	ラインなし

出力引数

p — 表示される多角形領域

Patch オブジェクト | Patch オブジェクトのベクトル

表示される多角形領域。Patch オブジェクトまたは Patch オブジェクトのベクトルとして返されます。各パッチはプロットされる 1 つの領域に対応します。領域をプロットした後でプロパティのクエリや変更を行うには、p を使用します。

代替機能

関数 patch を使用して 3 次元座標軸上に塗りつぶされた多角形を作成します。この関数では、塗りつぶされた領域を定義および構成するための次のいくつかの追加オプションが用意されています。

• 面と頂点のセットを指定して多角形を作成する。

• 同じ行列内に n が異なる複数の n 角形を指定する。

• カスタム RBG 値から面の色を内挿する。

拡張機能

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

fill3 関数は GPU 配列入力をサポートしますが、次の使用上の注意および制限があります。

• この関数は GPU 配列を受け入れますが、GPU 上では実行されません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

fill3 関数は分散配列をサポートしますが、次の使用上の注意および制限があります。

• この関数は分散配列に対して演算を行いますが、クライアントの MATLAB で実行されます。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

R2025a: 極座標での塗りつぶされた 3 次元パッチの作成

極座標で塗りつぶされた 3 次元パッチを作成するには、最初の引数として PolarAxes オブジェクトを指定します。

R2021a: 関数 fill と関数 fill3 で作成された Patch オブジェクトの XData、YData および ZData プロパティによって元のデータ型の値が返される

関数 fill または関数 fill3 で作成された Patch オブジェクトの XData、YData および ZData プロパティは、座標を double 値として返すのではなく、元の入力データ型を使用して返します。

以前のリリースでは、datetime 座標、duration 座標および categorical 座標は、XData、YData および ZData プロパティに格納される際に double 値に変換されます。

たとえば、次のコードは datetime の x 座標をもつ塗りつぶされた多角形を 3 次元座標軸上に作成します。次に、XData プロパティに格納されている値を使用して x2 を計算します。R2020b では、h.XData と x2 は double 配列です。R2021a では、h.XData と x2 は datetime 配列です。

x = datetime('01-Jan-2018') + days([0 1 1 0]);
y = [0 0 1 1];
z = [0 0 1 1];
h = fill3(x,y,z,'red');
x2 = h.XData + 1;

コード内で double 値を保持するには、Patch オブジェクトの Vertices プロパティから double 値を取得します。x 座標、y 座標および z 座標は、Vertices 配列の 1 列目、2 列目および 3 列目に double 値として格納されています。

x2 = h.Vertices(:,1) + 1;

あるいは、関数 ruler2num を使用します。座標値と対応する軸ルーラーを関数 ruler2num に渡します。

ax = gca;
x2 = ruler2num(h.XData,ax.XAxis) + 1;

参考

patch | fill | colormap | surf