カスタム深層学習層の定義
ヒント
このトピックでは、問題に合わせてカスタム深層学習層を定義する方法を説明します。Deep Learning Toolbox™ に組み込まれている層の一覧については、深層学習層の一覧を参照してください。
目的のタスクに必要な層が Deep Learning Toolbox に用意されていない場合、このトピックを指針として使用して独自のカスタム層を定義できます。カスタム層を定義した後、その層の有効性、GPU 互換性、定義した勾配の出力の正しさを自動的にチェックできます。
ニューラル ネットワーク層のアーキテクチャ
学習時には、ネットワークのフォワード パスとバックワード パスが反復して実行されます。
ネットワークのフォワード パスでは、各層は前の層の出力を取り、関数を適用し、結果を次の層に出力 (順伝播) します。また、LSTM 層などのステートフルな層では、層の状態を更新します。
層は複数の入力または出力を持つことができます。たとえば、層は複数の前の層から X1, …, XN を受け取り、出力 Y1, …, YM を後続の層に順伝播できます。
ネットワークのフォワード パスの最後に、ソフトウェアは予測とターゲットの間の損失 L を計算します。
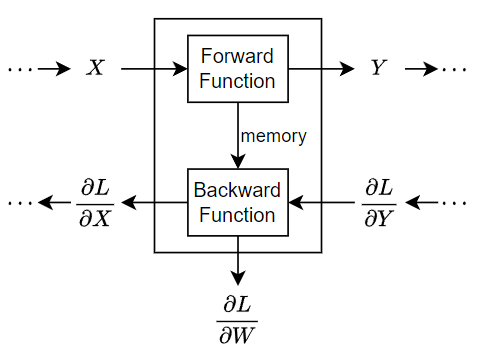
ネットワーク経由のバックワード パスでは、それぞれの層は、層の出力についての損失の微分を受け取り、入力についての損失 L の微分を計算し、その結果を逆伝播します。層に学習可能なパラメーターがある場合、層は層の重み (学習可能なパラメーター) の微分も計算します。ソフトウェアは、重みの微分を使用して学習可能なパラメーターを更新します。計算量を節約するために、順方向関数はオプションのメモリ出力を使用して逆方向関数と情報を共有できます。
次の図は、深層ニューラル ネットワークにおけるデータのフローを示すもので、1 つの入力 X、1 つの出力 Y、および学習可能なパラメーター W がある層経由のデータ フローを強調しています。
カスタム層テンプレート
カスタム層を定義するには、このクラス定義テンプレートを使用します。このテンプレートは、カスタム層のクラス定義の構造を提供します。概要は次のとおりです。
層のプロパティ、学習可能なパラメーター、状態パラメーターに関する、オプションの
propertiesブロック。詳細については、カスタム層のプロパティを参照してください。層のコンストラクター関数。
関数
predictとオプションの関数forward。詳細については、順方向関数を参照してください。状態プロパティをもつ層におけるオプションの関数
resetState。詳細については、リセット ステート関数を参照してください。オプションの関数
backward。詳細については、逆方向関数を参照してください。
classdef myLayer < nnet.layer.Layer % ... % & nnet.layer.Formattable ... % (Optional) % & nnet.layer.Acceleratable % (Optional) properties % (Optional) Layer properties. % Declare layer properties here. end properties (Learnable) % (Optional) Layer learnable parameters. % Declare learnable parameters here. end properties (State) % (Optional) Layer state parameters. % Declare state parameters here. end properties (Learnable, State) % (Optional) Nested dlnetwork objects with both learnable % parameters and state parameters. % Declare nested networks with learnable and state parameters here. end methods function layer = myLayer() % (Optional) Create a myLayer. % This function must have the same name as the class. % Define layer constructor function here. end function layer = initialize(layer,layout) % (Optional) Initialize layer learnable and state parameters. % % Inputs: % layer - Layer to initialize % layout - Data layout, specified as a networkDataLayout % object % % Outputs: % layer - Initialized layer % % - For layers with multiple inputs, replace layout with % layout1,...,layoutN, where N is the number of inputs. % Define layer initialization function here. end function [Y,state] = predict(layer,X) % Forward input data through the layer at prediction time and % output the result and updated state. % % Inputs: % layer - Layer to forward propagate through % X - Input data % Outputs: % Y - Output of layer forward function % state - (Optional) Updated layer state % % - For layers with multiple inputs, replace X with X1,...,XN, % where N is the number of inputs. % - For layers with multiple outputs, replace Y with % Y1,...,YM, where M is the number of outputs. % - For layers with multiple state parameters, replace state % with state1,...,stateK, where K is the number of state % parameters. % Define layer predict function here. end function [Y,state,memory] = forward(layer,X) % (Optional) Forward input data through the layer at training % time and output the result, the updated state, and a memory % value. % % Inputs: % layer - Layer to forward propagate through % X - Layer input data % Outputs: % Y - Output of layer forward function % state - (Optional) Updated layer state % memory - (Optional) Memory value for custom backward % function % % - For layers with multiple inputs, replace X with X1,...,XN, % where N is the number of inputs. % - For layers with multiple outputs, replace Y with % Y1,...,YM, where M is the number of outputs. % - For layers with multiple state parameters, replace state % with state1,...,stateK, where K is the number of state % parameters. % Define layer forward function here. end function layer = resetState(layer) % (Optional) Reset layer state. % Define reset state function here. end function [dLdX,dLdW,dLdSin] = backward(layer,X,Y,dLdY,dLdSout,memory) % (Optional) Backward propagate the derivative of the loss % function through the layer. % % Inputs: % layer - Layer to backward propagate through % X - Layer input data % Y - Layer output data % dLdY - Derivative of loss with respect to layer % output % dLdSout - (Optional) Derivative of loss with respect % to state output % memory - Memory value from forward function % Outputs: % dLdX - Derivative of loss with respect to layer input % dLdW - (Optional) Derivative of loss with respect to % learnable parameter % dLdSin - (Optional) Derivative of loss with respect to % state input % % - For layers with state parameters, the backward syntax must % include both dLdSout and dLdSin, or neither. % - For layers with multiple inputs, replace X and dLdX with % X1,...,XN and dLdX1,...,dLdXN, respectively, where N is % the number of inputs. % - For layers with multiple outputs, replace Y and dLdY with % Y1,...,YM and dLdY,...,dLdYM, respectively, where M is the % number of outputs. % - For layers with multiple learnable parameters, replace % dLdW with dLdW1,...,dLdWP, where P is the number of % learnable parameters. % - For layers with multiple state parameters, replace dLdSin % and dLdSout with dLdSin1,...,dLdSinK and % dLdSout1,...,dldSoutK, respectively, where K is the number % of state parameters. % Define layer backward function here. end end end
形式を整えた入出力
dlarray オブジェクトを使用すると、次元にラベルを付けることができるため、高次元のデータをより簡単に扱うことができます。たとえば、"S"、"T"、"C"、"B" のラベルを使用して、各次元が空間、時間、チャネル、バッチのどの次元に対応するかを示すことができます。特に指定がないその他の次元については、ラベル "U" を使用します。特定の次元に対して演算を行うオブジェクト関数 dlarray の場合、dlarray オブジェクトの形式を直接整えるか、DataFormat オプションを使用することで、次元ラベルを指定できます。
形式を整えた dlarray オブジェクトを層関数で使用することで、次元の並べ替え、追加、削除を行う層など、入力と出力の形式が異なる層を定義することもできます。たとえば、形式が "SSCB" (spatial、spatial、channel、batch) であるイメージのミニバッチを入力として受け取り、形式が "CBT" (channel、batch、time) であるシーケンスのミニバッチを出力する層を定義できます。形式を整えた dlarray オブジェクトを使用すると、入力形式が異なるデータの処理が可能な層を定義することもできます。たとえば、形式 "SSCB" (spatial、spatial、channel、batch) と "CBT" (channel、batch、time) の入力をサポートする層を定義できます。
nnet.layer.Formattable クラスからの継承を選択することで、ソフトウェアが層とデータをやり取りする際に、形式を整えたデータや形式を整えていないデータをどのように処理するかを指定できます。次の表は、ソフトウェアがカスタム層内の形式を整えたデータと形式を整えていないデータを処理する方法を示しています。
| 層の定義 | 入力データの処理 | 出力データの処理 |
|---|---|---|
nnet.layer.Formattable から継承する | ソフトウェアは層入力を層関数に直接渡します。
| ソフトウェアは層関数の出力を後続の層に直接渡します。
警告
|
nnet.layer.Formattable から継承しない | ソフトウェアは形式を整えた入力から形式を削除し、形式を整えていないデータを層関数に渡します。
| 出力データの形式は整っていてはなりません。ソフトウェアは、形式を整えていない層関数の出力に層入力の形式を適用し、その結果を後続の層に渡します。
|
形式を整えた入力をもつカスタム層の定義方法を示す例については、形式を整えた入力をもつカスタム深層学習層の定義を参照してください。
カスタム層の高速化
カスタム層の定義時に逆方向関数を指定しない場合、自動微分を使用して勾配が自動的に決定されます。
逆方向関数がないカスタム層でネットワークに学習させる場合、カスタム層の順方向関数の各 dlarray 入力オブジェクトがトレースされ、自動微分に使用される計算グラフが決定されます。このトレース処理には時間がかかる場合があります。また、同じトレースが繰り返し計算される場合があります。トレースの最適化、キャッシュ、再利用を行うことで、ネットワーク学習時の勾配計算を高速化できます。また、学習後にこれらのトレースは再利用され、ネットワーク予測が高速化されます。
トレースは、層入力のサイズ、形式、基となるデータ型によって異なります。つまり、入力のサイズ、形式、基となるデータ型がキャッシュに含まれていない場合、層によって新しいトレースがトリガーされます。既にキャッシュされているトレースに対して入力の値のみが異なる場合、新しいトレースはトリガーされません。
カスタム層が高速化をサポートするように指定するには、カスタム層の定義時に nnet.layer.Acceleratable クラスからも継承します。nnet.layer.Acceleratable からカスタム層を継承すると、dlnetwork オブジェクトを使ってデータを渡すときにトレースが自動的にキャッシュされます。
たとえば、カスタム層 myLayer が高速化をサポートするように指定するには、次の構文を使用します。
classdef myLayer < nnet.layer.Layer & nnet.layer.Acceleratable ... end
高速化の考慮事項
トレースのキャッシュの特性上、すべての関数が高速化をサポートしているわけではありません。
キャッシュ プロセスでは、変更される可能性がある、または外部の要因に左右される値またはコード構造がキャッシュされる場合があります。以下のようなカスタム層を高速化する際は、注意が必要です。
乱数を生成する。
dlarrayオブジェクトの値によって決まる条件を含むifステートメントやwhileループを使用する。
キャッシュ プロセスでは計算が追加されるため、場合によっては、高速化によってコードの実行時間が長くなってしまうことがあります。このシナリオは、再利用できない新しいキャッシュを作成することに頻繁に時間が費やされる場合に発生します。たとえば、シーケンス長が異なる複数のミニバッチを関数に渡すと、それぞれのシーケンス長ごとに新しいトレースがトリガーされます。
カスタム層の高速化によって速度が低下する場合は、Acceleratable クラスを削除して高速化を無効にするか、Acceleration オプションを "none" に設定して dlnetwork オブジェクトの関数 predict と forward の高速化を無効にしてください。
カスタム層の高速化サポートを有効にする方法の詳細については、Custom Layer Function Accelerationを参照してください。
カスタム層のプロパティ
層のプロパティはクラス定義の properties セクションで宣言します。
既定では、カスタム層には次のプロパティがあります。これらのプロパティを properties セクションで宣言しないでください。
| Property | 説明 |
|---|---|
Name | 層の名前。文字ベクトルまたは string スカラーとして指定します。Layer 配列入力の場合、trainnet 関数および dlnetwork 関数は、名前のない層に自動的に名前を割り当てます。 |
Description | 層についての 1 行の説明。string スカラーまたは文字ベクトルとして指定します。この説明は、 層の説明を指定しない場合、層のクラス名が表示されます。 |
Type | 層の型。文字ベクトルまたは string スカラーとして指定します。 層のタイプを指定しない場合、層のクラス名が表示されます。 |
NumInputs | 層の入力の数。正の整数として指定します。この値を指定しない場合、NumInputs は InputNames の名前の数に自動的に設定されます。既定値は 1 です。 |
InputNames | 層の入力の名前。文字ベクトルの cell 配列として指定します。この値を指定せず、NumInputs が 1 より大きい場合、InputNames は {'in1',...,'inN'} に自動的に設定されます。ここで、N = NumInputs です。既定値は {'in'} です。 |
NumOutputs | 層の出力の数。正の整数として指定します。この値を指定しない場合、NumOutputs は OutputNames の名前の数に自動的に設定されます。既定値は 1 です。 |
OutputNames | 層の出力の名前。文字ベクトルの cell 配列として指定します。この値を指定せず、NumOutputs が 1 より大きい場合、OutputNames は {'out1',...,'outM'} に自動的に設定されます。ここで、M = NumOutputs です。既定値は {'out'} です。 |
層にその他のプロパティがない場合は、properties セクションを省略できます。
ヒント
複数の入力がある層を作成する場合、層のコンストラクターで NumInputs と InputNames のいずれかのプロパティを設定しなければなりません。複数の出力がある層を作成している場合、層のコンストラクターで NumOutputs と OutputNames のいずれかのプロパティを設定しなければなりません。例については、複数の入力があるカスタム深層学習層の定義を参照してください。
学習可能なパラメーター
層の学習可能なパラメーターはクラス定義の properties (Learnable) セクションで宣言します。
学習可能なパラメーターとして、数値配列または dlnetwork オブジェクトを指定できます。dlnetwork オブジェクトが学習可能なパラメーターと状態パラメーターの両方をもつ場合 (たとえば、LSTM 層をもつ dlnetwork オブジェクトの場合)、properties (Learnable, State) セクションでこれを指定する必要があります。層に学習可能なパラメーターがない場合は、Learnable 属性をもつ properties セクションを省略できます。
オプションで、学習可能なパラメーターの学習率係数および L2 係数を指定できます。既定では、それぞれの学習可能なパラメーターの学習率係数と L2 係数は 1 に設定されています。組み込みの層とカスタム層のどちらの場合も、以下の関数を使用して、学習率係数と L2 正則化係数を設定および取得できます。
| 関数 | 説明 |
|---|---|
setLearnRateFactor | 学習可能なパラメーターの学習率係数を設定します。 |
setL2Factor | 学習可能なパラメーターの L2 正則化係数を設定します。 |
getLearnRateFactor | 学習可能なパラメーターの学習率係数を取得します。 |
getL2Factor | 学習可能なパラメーターの L2 正則化係数を取得します。 |
学習可能なパラメーターの学習率係数および L2 係数を指定するには、構文 layer = setLearnRateFactor(layer,parameterName,value) および layer = setL2Factor(layer,parameterName,value) をそれぞれ使用します。
学習可能なパラメーターの学習率係数および L2 係数の値を取得するには、構文 getLearnRateFactor(layer,parameterName) および getL2Factor(layer,parameterName) をそれぞれ使用します。
たとえば、この構文は、学習可能なパラメーター "Alpha" の学習率係数を 0.1 に設定します。
layer = setLearnRateFactor(layer,"Alpha",0.1);状態パラメーター
再帰層などのステートフルな層の場合、層の状態パラメーターはクラス定義の properties (State) セクションで宣言します。学習可能なパラメーターが、学習可能なパラメーターと状態パラメーターの両方をもつ dlnetwork オブジェクトの場合 (たとえば、LSTM 層をもつ dlnetwork オブジェクトの場合)、対応するプロパティを properties (Learnable, State) セクションで指定する必要があります。層に状態パラメーターがない場合は、State 属性をもつ properties セクションを省略できます。
層に状態パラメーターがある場合、順方向関数によって、更新された層の状態が返されなければなりません。詳細については、順方向関数を参照してください。
カスタムのリセット ステート関数を指定するには、構文 layer = resetState(layer) を使用してクラス定義に関数を追加します。詳細については、リセット ステート関数を参照してください。
関数 trainnet を使用して、状態パラメーターをもつカスタム層が含まれるネットワークに並列学習させることはできません。状態パラメーターをもつカスタム層があるネットワークに学習させるには、ExecutionEnvironment 学習オプションが "auto"、"gpu"、または "cpu" でなければなりません。
学習可能なパラメーターと状態パラメーターの初期化
層のコンストラクター関数内またはカスタム関数 initialize 内で、層の学習可能なパラメーターと状態を初期化するよう指定できます。
学習可能なパラメーターまたは状態パラメーターの初期化において、層の入力からサイズ情報を取得する必要がない場合 (たとえば、重み付き加算層の学習可能なパラメーターの重みが、層の入力数に等しいサイズをもつベクトルである場合)、層のコンストラクター関数内で重みを初期化できます。例については、複数の入力があるカスタム深層学習層の定義を参照してください。
学習可能なパラメーターまたは状態パラメーターの初期化において、層の入力からサイズ情報を取得する必要がある場合 (たとえば、SReLU 層の学習可能なパラメーターの重みが、入力データのチャネル数に等しいサイズをもつベクトルである場合)、入力データ レイアウトに関する情報を利用するカスタム初期化関数内で重みを初期化できます。例については、学習可能なパラメーターを含むカスタム深層学習層の定義を参照してください。
順方向関数
層によっては学習時と予測時の動作が異なる場合があります。たとえば、ドロップアウト層は学習時にのみドロップアウトを行い、予測時には何の影響も与えません。層は、フォワード パスを実行するために 2 つの関数 predict と forward のいずれかを使用します。フォワード パスが予測時に発生する場合、層は関数 predict を使用します。フォワード パスが学習時に発生する場合、層は関数 forward を使用します。予測時と学習時で異なる 2 つの関数を必要としない場合は、関数 forward を省略できます。この場合、学習時に層は predict を使用します。
層に状態パラメーターがある場合、順方向関数によって、更新された層の状態パラメーターが数値配列として返されなければなりません。
カスタム関数 forward とカスタム関数 backward の両方を定義する場合、順方向関数によって、memory 出力が返されなければなりません。
関数 predict の構文は、層のタイプによって異なります。
Y = predict(layer,X)は、層を介して入力データXを転送し、結果Yを出力します。この場合、layerは、1 つの入力と 1 つの出力をもちます。[Y,state] = predict(layer,X)は、更新された状態パラメーターstateも出力します。この場合、layerは 1 つの状態パラメーターをもちます。
複数の入力、複数の出力、または複数の状態パラメーターを使用して、層の構文を調整できます。
複数の入力をもつ層の場合、
XをX1,...,XNに置き換えます。ここで、Nは入力の数です。NumInputsプロパティはNと一致しなければなりません。複数の出力をもつ層の場合、
YをY1,...,YMに置き換えます。ここで、Mは出力の数です。NumOutputsプロパティはMと一致しなければなりません。複数の状態パラメーターをもつ層の場合、
stateをstate1,...,stateKに置き換えます。ここで、Kは状態パラメーターの数です。
ヒント
層への入力の数が変化する可能性がある場合、X1,…,XN ではなく varargin を使用します。この場合、varargin は入力の cell 配列です。ここで、varargin{i} は Xi に対応します。
出力の数が変化する可能性がある場合、Y1,…,YM ではなく varargout を使用します。この場合、varargout は出力の cell 配列です。ここで、varargout{j} は Yj に対応します。
ヒント
学習可能なパラメーターの dlnetwork オブジェクトがカスタム層にある場合、カスタム層の関数 predict 内で、dlnetwork の関数 predict を使用します。これを行うと、dlnetwork オブジェクトの関数 predict は適切な層処理を使用して予測を行います。dlnetwork に状態パラメーターがある場合、ネットワークの状態も返します。
関数 forward の構文は、層のタイプによって異なります。
Y = forward(layer,X)は、層を介して入力データXを転送し、結果Yを出力します。この場合、layerは、1 つの入力と 1 つの出力をもちます。[Y,state] = forward(layer,X)は、更新された状態パラメーターstateも出力します。この場合、layerは 1 つの状態パラメーターをもちます。[__,memory] = forward(layer,X)は、前述の構文のいずれかを使用して、カスタム関数backwardのメモリ値も返します。カスタム関数forwardとカスタム関数backwardの両方が層に存在する場合、順方向関数によってメモリ値が返されなければなりません。
複数の入力、複数の出力、または複数の状態パラメーターを使用して、層の構文を調整できます。
複数の入力をもつ層の場合、
XをX1,...,XNに置き換えます。ここで、Nは入力の数です。NumInputsプロパティはNと一致しなければなりません。複数の出力をもつ層の場合、
YをY1,...,YMに置き換えます。ここで、Mは出力の数です。NumOutputsプロパティはMと一致しなければなりません。複数の状態パラメーターをもつ層の場合、
stateをstate1,...,stateKに置き換えます。ここで、Kは状態パラメーターの数です。
ヒント
層への入力の数が変化する可能性がある場合、X1,…,XN ではなく varargin を使用します。この場合、varargin は入力の cell 配列です。ここで、varargin{i} は Xi に対応します。
出力の数が変化する可能性がある場合、Y1,…,YM ではなく varargout を使用します。この場合、varargout は出力の cell 配列です。ここで、varargout{j} は Yj に対応します。
ヒント
学習可能なパラメーターの dlnetwork オブジェクトがカスタム層にある場合、カスタム層の関数 forward 内で、dlnetwork オブジェクトの関数 forward を使用します。これを行うと、dlnetwork オブジェクトの関数 forward は適切な層処理を使用して学習を行います。
入力の次元は、データのタイプと結合層の出力によって異なります。
| 層入力 | 例 | |
|---|---|---|
| 形状 | データ形式 | |
| 2 次元イメージ | h×w×c×N の数値配列。ここで、h、w、c、および N は、それぞれイメージの高さ、幅、チャネル数、および観測値の数です。 | "SSCB" |
| 3 次元イメージ | h×w×d×c×N の数値配列。ここで、h、w、d、c、および N は、それぞれイメージの高さ、幅、深さ、チャネル数、およびイメージの観測値の数です。 | "SSSCB" |
| ベクトル シーケンス | c×N×s の行列。ここで、c はシーケンスの特徴の数、N はシーケンスの観測値の数、s はシーケンス長です。 | "CBT" |
| 2 次元イメージ シーケンス | h×w×c×N×s の配列。ここで、h、w、および c はそれぞれイメージの高さ、幅、およびチャネル数に対応し、N はイメージ シーケンスの観測値の数、s はシーケンス長です。 | "SSCBT" |
| 3 次元イメージ シーケンス | h×w×d×c×N×s の配列。ここで、h、w、d、および c はそれぞれイメージの高さ、幅、深さ、チャネル数に対応し、N はイメージ シーケンスの観測値の数、s はシーケンスの長さです。 | "SSSCBT" |
| 特徴 | c 行 N 列の配列。ここで、c は特徴の数、N は観測値の数です。 | "CB" |
シーケンスを出力する層の場合、その層は、任意の長さのシーケンス、または時間次元をもたないデータを出力できます。
カスタム層順方向関数の出力は複素数値にすることができます。 (R2024a 以降)層が複素数値データを出力する場合、ニューラル ネットワークでカスタム層を使用するときに、後続の層または損失関数が複素数値入力をサポートしていることを確認しなければなりません。カスタム層の関数 predict または関数 forward で複素数を使用すると、学習可能なパラメーターが複素数になる可能性があります。複素数値の学習可能なパラメーターを使用してモデルに学習させるには、関数 trainnet を "sgdm" ソルバー、"adam" ソルバー、または "rmsprop" ソルバーと共に使用し、関数 trainingOptions を使用してそれらを指定するか、関数 sgdmupdate、adamupdate、または rmspropupdate でカスタム学習ループを使用します。
R2024a より前: カスタム層順方向関数の出力は複素数であってはなりません。カスタム層の関数 predict または関数 forward に複素数が含まれる場合は、すべての出力を実数値に変換してから返します。カスタム層の関数 predict または関数 forward で複素数を使用すると、学習可能なパラメーターが複素数になる可能性があります。自動微分を使用する場合 (つまり、カスタム層の逆方向関数を記述するのでない場合)、関数の計算を開始する時点で、学習可能なすべてのパラメーターを実数値に変換します。これにより、自動微分アルゴリズムが複素数値の勾配を出力することはなくなります。
リセット ステート関数
dlnetwork オブジェクトの関数 resetState は、既定では状態パラメーターをもつカスタム層に影響を与えません。ネットワーク オブジェクトの関数 resetState が層に対して行う動作を定義するには、状態パラメーターをリセットするオプションの層関数 resetState を層定義の中に定義します。
関数 resetState の構文は layer = resetState(layer) でなければなりません。ここで、返される層はリセットされた状態プロパティをもちます。
関数 resetState では、学習可能なパラメーターと状態パラメーターを除く層プロパティを設定してはなりません。この関数でそれ以外の層プロパティを設定した場合、層は予期せぬ動作をする可能性があります。 (R2023a 以降)
逆方向関数
層の逆方向関数は、入力データについての損失の微分を計算し、結果を前の層に出力 (逆伝播) します。層に学習可能なパラメーター (層の重みなど) がある場合、backward は学習可能なパラメーターの微分も計算します。関数 trainnet を使用すると、層は、バックワード パスの間にこれらの微分を使用して学習可能なパラメーターを自動的に更新します。
逆方向関数の定義はオプションです。逆方向関数を指定せず、層の順方向関数が dlarray オブジェクトをサポートしている場合、自動微分を使用して逆方向関数が自動的に決定されます。dlarray オブジェクトをサポートしている関数の一覧については、dlarray をサポートする関数の一覧を参照してください。次のことを行う場合、カスタム逆方向関数を定義します。
特定のアルゴリズムを使用して微分を計算する。
dlarrayオブジェクトをサポートしない順方向関数で演算を使用する。
学習可能なパラメーターを持つ dlnetwork オブジェクトを含むカスタム層では、カスタム逆方向関数がサポートされていません。
カスタム逆方向関数を定義するには、backward という名前の関数を作成します。
関数 backward の構文は、層のタイプによって異なります。
dLdX = backward(layer,X,Y,dLdY,memory)は、層入力についての損失の微分dLdXを返します。この場合、layerは 1 つの入力と 1 つの出力をもちます。Yは順方向関数の出力に対応し、dLdYはYについての損失の微分に対応します。関数の入力memoryは、順方向関数のメモリ出力に対応します。[dLdX,dLdW] = backward(layer,X,Y,dLdY,memory)は、学習可能なパラメーターについての損失の微分dLdWも返します。この場合、layerは 1 つの学習可能なパラメーターをもちます。[dLdX,dLdSin] = backward(layer,X,Y,dLdY,dLdSout,memory)は、状態入力についての損失の微分dLdSinも返します。この場合、layerは 1 つの状態パラメーターをもちます。dLdSoutは層の状態出力についての損失の微分に対応します。[dLdX,dLdW,dLdSin] = backward(layer,X,Y,dLdY,dLdSout,memory)は、学習可能なパラメーターについての損失の微分dLdW、および層の状態入力についての損失の微分dLdSinも返します。この場合、layerは 1 つの状態パラメーターと 1 つの学習可能なパラメーターをもちます。
複数の入力、複数の出力、複数の学習可能なパラメーター、または複数の状態パラメーターを使用して、層の構文を調整できます。
複数の入力をもつ層の場合、
XとdLdXをそれぞれX1,...,XNとdLdX1,...,dLdXNに置き換えます。ここで、Nは入力の数です。複数の出力をもつ層の場合、
YとdLdYをそれぞれY1,...,YMとdLdY1,...,dLdYMに置き換えます。ここで、Mは出力の数です。複数の学習可能なパラメーターをもつ層の場合、
dLdWをdLdW1,...,dLdWPに置き換えます。ここで、Pは学習可能なパラメーターの数です。複数の状態パラメーターをもつ層の場合、
dLdSinとdLdSoutをそれぞれdLdSin1,...,dLdSinKとdLdSout1,...,dLdSoutKに置き換えます。ここで、Kは状態パラメーターの数です。
フォワード パスとバックワード パスの間に使用されない変数が保存されることを防いでメモリ使用量を削減するには、対応する入力引数を ~ に置き換えます。
ヒント
backward への入力の数が変化する可能性がある場合、layer の後に入力引数ではなく varargin を使用します。この場合、varargin は入力の cell 配列になります。ここで、最初の N 個の要素は N 個の層入力に対応し、その次の M 個の要素は M 個の層出力に対応し、その次の M 個の要素は M 個の層出力についての損失の微分に対応し、その次の K 個の要素は K 個の状態出力についての損失に関する K 個の微分に対応し、最後の要素は memory に対応します。
出力の数が変化する可能性がある場合、出力引数ではなく varargout を使用します。この場合、varargout は出力の cell 配列になります。ここで、最初の N 個の要素は N 個の層入力についての損失に関する N 個の微分に対応し、その次の P 個の要素は P 個の学習可能なパラメーターについての損失の微分に対応し、その次の K 個の要素は K 個の状態入力についての損失の微分に対応します。
X と Y の値は順方向関数の場合と同じです。dLdY の次元は Y の次元と同じです。
dLdX の次元およびデータ型は、X の次元およびデータ型と同じです。dLdW の次元およびデータ型は、W の次元およびデータ型と同じです。
入力データに対する損失の微分を計算するには、出力データに対する損失の微分と入力データに対する出力データの微分を使って、連鎖律を使用できます。
関数 trainnet を使用する場合、層は、バックワード パスの間に微分 dLdW を使用して学習可能なパラメーターを自動的に更新します。
カスタム逆方向関数の定義方法を示す例については、カスタム層の逆方向関数の指定を参照してください。
カスタム層逆方向関数の出力は複素数値にすることができます。 (R2024a 以降)複素数値の勾配を使用すると、学習可能なパラメーターが複素数になる場合があります。複素数値の学習可能なパラメーターを使用してモデルに学習させるには、関数 trainnet を "sgdm" ソルバー、"adam" ソルバー、または "rmsprop" ソルバーと共に使用し、関数 trainingOptions を使用してそれらを指定するか、関数 sgdmupdate、adamupdate、または rmspropupdate でカスタム学習ループを使用します。
R2024a より前: カスタム層逆方向関数の出力は複素数であってはなりません。逆方向関数に複素数が含まれる場合は、逆方向関数のすべての出力を実数値に変換してから返します。
GPU 互換性
層の順方向関数が dlarray オブジェクトを完全にサポートしている場合、層は GPU 互換です。そうでない場合、GPU 互換にするには、層関数が入力をサポートし、gpuArray (Parallel Computing Toolbox) 型の出力を返さなければなりません。
多くの MATLAB® 組み込み関数が入力引数 gpuArray (Parallel Computing Toolbox) および dlarray をサポートしています。dlarray オブジェクトをサポートしている関数の一覧については、dlarray をサポートする関数の一覧を参照してください。GPU で実行される関数の一覧については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。深層学習に GPU を使用するには、サポートされている GPU デバイスもなければなりません。サポートされているデバイスの詳細については、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。MATLAB での GPU の使用の詳細は、MATLAB での GPU 計算 (Parallel Computing Toolbox)を参照してください。
コード生成の互換性
コード生成用のカスタム層を作成するには、層の定義でプラグマ %#codegen を指定しなければなりません。コード生成は、状態プロパティ (属性が State であるプロパティ) をもつカスタム層をサポートしません。
さらに、サードパーティのライブラリを使用するコードを生成する場合は、次の点に注意してください。
コード生成では、2 次元イメージ入力または特徴入力のみをもつカスタム層がサポートされます。
層の順方向関数の入力と出力は、同じバッチ サイズでなければなりません。
非スカラーのプロパティは、single、double、または文字配列でなければなりません。
スカラーのプロパティは、数値型、logical 型、または string 型でなければなりません。
コード生成をサポートするカスタム層を作成する方法を示す例については、コード生成用のカスタム深層学習層の定義を参照してください。
ネットワーク構成
それ自体がニューラル ネットワークを定義するカスタム層を作成するには、層定義の properties (Learnable) セクションで、学習可能なパラメーターとして dlnetwork オブジェクトを宣言します。この手法は "ネットワーク構成" と呼ばれます。以下の場合にネットワーク構成を使用できます。
コントロール フローをもつネットワーク (入力データに応じて動的に変更できるセクションをもつネットワークなど) の作成。
ループをもつネットワーク (自分自身に出力をフィードバックするセクションをもつネットワークなど) の作成。
重みの共有の実装 (ツイン ニューラル ネットワークや敵対的生成ネットワーク (GAN) など、異なるデータが同じ層を通過する必要があるネットワークなどにおいて)。
学習可能なパラメーターと状態パラメーターの両方をもつ入れ子ネットワーク (たとえば、バッチ正規化層または LSTM 層をもつネットワークなど) の場合は、層定義の properties (Learnable, State) セクションでネットワークを宣言します。
層の有効性のチェック
カスタム深層学習層を作成する場合、関数 checkLayer を使用して、層が有効であることをチェックできます。この関数は、層について、有効性、GPU 互換性、勾配定義の正しさ、コード生成の互換性をチェックします。層が有効であることをチェックするには、次のコマンドを実行します。
checkLayer(layer,layout)
layer は層のインスタンス、layout は層への入力に対して有効なサイズとデータ形式を指定する networkDataLayout オブジェクトです。複数の観測値をチェックするには、ObservationDimension オプションを使用します。コード生成の互換性チェックを実行するには、CheckCodegenCompatibility オプションを 1 (true) に設定します。入力サイズが大きい場合、勾配チェックの実行に時間がかかります。チェックを高速化するには、指定する有効な入力サイズを小さくします。詳細については、カスタム層の有効性のチェックを参照してください。
checkLayer を使用したカスタム層の有効性のチェック
カスタム層 sreluLayer について層の有効性をチェックします。
この例にサポート ファイルとして添付されているカスタム層 sreluLayer は、入力データに SReLU 演算を適用します。この層にアクセスするには、この例をライブ スクリプトとして開きます。
層のインスタンスを作成します。
layer = sreluLayer;
層への典型的な入力に要求される入力サイズと形式を指定する networkDataLayout オブジェクトを作成します。有効な入力サイズとして [24 24 20 128] を指定します。ここで、各次元は、前の層の出力における高さ、幅、チャネル数、および観測値の数に対応します。形式を "SSCB" (空間、空間、チャネル、バッチ) として指定します。
validInputSize = [24 24 20 128];
layout = networkDataLayout(validInputSize,"SSCB");checkLayer を使用して、層の有効性をチェックします。
checkLayer(layer,layout)
Skipping GPU tests. No compatible GPU device found. Skipping code generation compatibility tests. To check validity of the layer for code generation, specify the CheckCodegenCompatibility and ObservationDimension options. Running nnet.checklayer.TestLayerWithoutBackward .......... .......... Done nnet.checklayer.TestLayerWithoutBackward __________ Test Summary: 20 Passed, 0 Failed, 0 Incomplete, 14 Skipped. Time elapsed: 0.16436 seconds.
この関数によって層に関する問題は検出されていません。
参考
trainnet | trainingOptions | dlnetwork | functionLayer | checkLayer | setLearnRateFactor | setL2Factor | getLearnRateFactor | getL2Factor | findPlaceholderLayers | replaceLayer | PlaceholderLayer | networkDataLayout