自己組織化マップニューラルネットワークによるクラスター化

自己組織化特徴マップ (SOFM) は、入力空間でのグループ化の方法に従った入力ベクトルの分類を学習します。これは、自己組織化マップの隣接するニューロンが入力空間の隣接するセクションを認識するように学習するという点で、競合層とは異なります。そのため、自己組織化マップは分布 (競合層と同様) と、学習を行う入力ベクトルのトポロジの両方を学習します。

SOFM の層内のニューロンは、最初はトポロジ関数に従って、物理的な位置に配置されます。関数 gridtop、hextop、randtop は、ニューロンをそれぞれグリッドトポロジ、六角形トポロジ、ランダムトポロジに配置できます。ニューロン間の距離は、それらの位置から距離関数で計算されます。距離関数には dist、boxdist、linkdist、および mandist の 4 つがあります。リンク距離が最も一般的です。これらのトポロジと距離関数については、トポロジ (gridtop、hextop、randtop)と距離関数 (dist、linkdist、mandist、boxdist)で説明します。

ここで、自己組織化特徴マップネットワークは、競合層で使用したものと同じ手順で勝者ニューロン i* を識別します。ただし、勝者ニューロンのみを更新するのではなく、勝者ニューロンの近傍 N_i_* (d) 内のすべてのニューロンが Kohonen 規則を使用して更新されます。具体的には、そのようなすべてのニューロン i ∊ N_i_* (d) は次のように調整されます。

${}_{i}w (q) = {}_{i}w (q - 1) + α (p (q) - {}_{i}w (q - 1))$

または

${}_{i}w (q) = (1 - α) {}_{i}w (q - 1) + α p (q)$

ここで、"近傍" N_i_* (d) には、勝者ニューロン i* の半径 d 内にあるすべてのニューロンのインデックスが含まれます。

$N_{i} (d) = {j, d_{i j} \leq d}$

そのため、ベクトル p が与えられると、勝者ニューロンの重み "および" その近傍が p の方向に移動します。結果として、多くが与えられると、近傍のニューロンはお互いに似たベクトルを学習しています。

"バッチアルゴリズム" と呼ばれる、SOFM 学習の別のバーションでは、重みが更新される前にデータセット全体をネットワークに与えます。このアルゴリズムは次に、各入力ベクトルに対する勝者ニューロンを決定します。その後、各重みベクトルは、自身が勝者であるか、勝者の近傍にあるような入力ベクトルすべての平均位置の方向に移動します。

近傍の概念を説明するために、下の図で考えてみましょう。左側の図は、ニューロン 13 の周囲の半径 d = 1 の 2 次元近傍を示しています。右側の図は、半径 d = 2 の近傍を示しています。

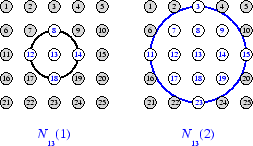
Side by side diagrams each showing a two-dimensional neighborhood of radius d.

これらの近傍は、N₁₃(1) = {8, 12, 13, 14, 18} や
N₁₃(2) = {3, 7, 8, 9, 11, 12, 13, 14, 15, 17, 18, 19, 23} のように記述できます。

SOFM 内のニューロンは、2 次元パターンに配置する必要はありません。1 次元配置または 3 次元以上の配置を使用できます。1 次元 SOFM の場合、ニューロンは半径 1 の中に 2 つの近傍しかありません (またはニューロンが線の終点ならば近傍は 1 つです)。たとえば、ニューロンと近傍の長方形や六角形の配置を使用して、別の方法で距離を定義することもできます。ネットワーク性能は、近傍の正確な形状には左右されません。

トポロジ (`gridtop`、`hextop`、`randtop`)

関数 gridtop、hextop、および randtop を使用して、元のニューロンの位置に対して別のトポロジを指定できます。

gridtop トポロジは、前の図に示したものに似た長方形グリッドのニューロンで始まります。たとえば、6 個のニューロンから成る 2 x 3 の配列にするとします。これは次のように実現できます。

pos = gridtop([2, 3])
pos =
     0     1     0     1     0     1
     0     0     1     1     2     2

ここで、ニューロン 1 は位置 (0,0)、ニューロン 2 は位置 (1,0)、ニューロン 3 は位置 (0,1) などのようになります。

Plot showing the positions of six neurons arranged in a 2-by-3 grid.

次元のサイズを反転して gridtop を呼び出すと、わずかに異なる配置になることに注意してください。

pos = gridtop([3, 2])
pos =
     0     1     2     0     1     2
     0     0     0     1     1     1

次のコードを使用して、gridtop トポロジで 8 x 10 のニューロンのセットを作成できます。

pos = gridtop([8 10]);
plotsom(pos)

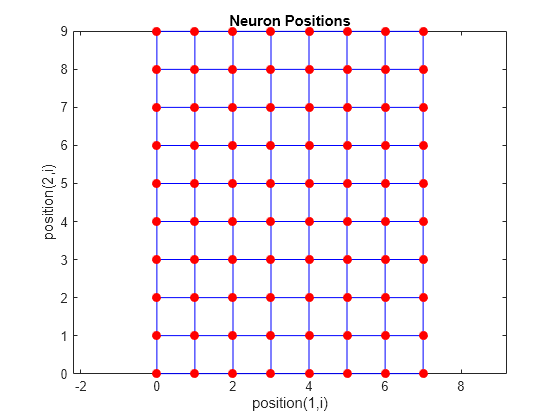
Figure contains an axes object. The axes object with title Neuron Positions, xlabel position(1,i), ylabel position(2,i) contains 2 objects of type line. One or more of the lines displays its values using only markers

ご覧のように、gridtop トポロジのニューロンは、実際にグリッド上にあります。

関数 hextop では、類似のニューロンのセットが作成されますが、六角形パターンになります。2 x 3 パターンの hextop ニューロンは、次のように生成されます。

pos = hextop([2, 3])
pos =
         0    1.0000    0.5000    1.5000         0    1.0000
         0         0    0.8660    0.8660    1.7321    1.7321

hextop は、selforgmap によって生成される SOM ネットワークに対する既定のパターンであることに注意してください。

次のコードを使用して、hextop トポロジで 8 x 10 のニューロンのセットを作成してプロットできます。

pos = hextop([8 10]);
plotsom(pos)

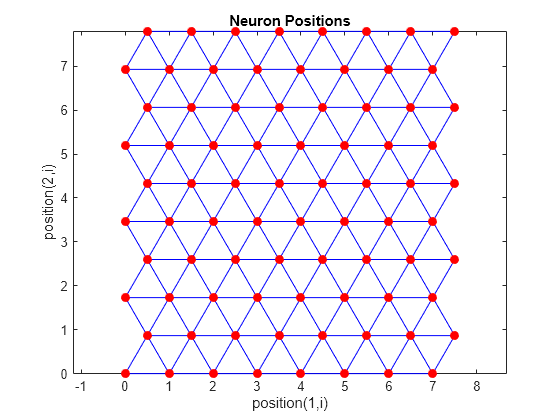
ニューロンの位置が六角形の配置になっていることに注意してください。

最後に、関数 randtop では、N 次元のランダムパターンのニューロンが作成されます。次のコードによって、ニューロンのランダムパターンが生成されます。

pos = randtop([2, 3])
pos =
         0    0.7620    0.6268    1.4218    0.0663    0.7862
    0.0925         0    0.4984    0.6007    1.1222    1.4228

次のコードを使用して、randtop トポロジで 8 x 10 のニューロンのセットを作成してプロットできます。

pos = randtop([8 10]);
plotsom(pos)

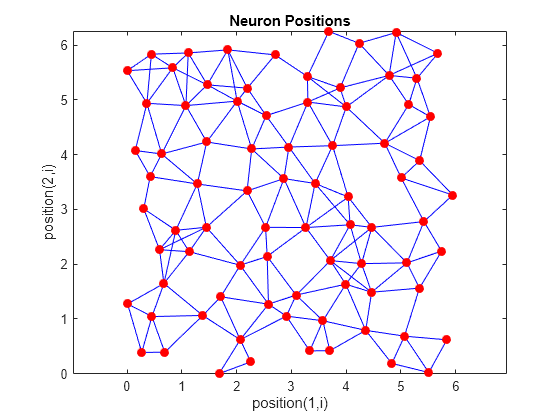
例については、これらのトポロジ関数のヘルプを参照してください。

距離関数 (`dist`、`linkdist`、`mandist`、`boxdist`)

このツールボックスでは、特定のニューロンからその近傍への距離を計算するための方法が 4 種類あります。それぞれの計算手法は、特殊関数で実装されています。

関数 dist では、"ホーム" ニューロンから他のニューロンまでのユークリッド距離が計算されます。3 個のニューロンがあるとします。

pos2 = [0 1 2; 0 1 2]
pos2 =
     0     1     2
     0     1     2

次を使用して、各ニューロンから他のニューロンまでの距離を求めます。

D2 = dist(pos2)
D2 =
         0    1.4142    2.8284
    1.4142         0    1.4142
    2.8284    1.4142         0

このように、ニューロン 1 からそれ自身までの距離は 0、ニューロン 1 からニューロン 2 までの距離は 1.4142 などとなります。

以下のグラフには、複数のニューロンから成る 2 次元 (gridtop) 層のホームニューロンを示しています。ホームニューロンには、その周囲に直径の増加に対応する近傍があります。直径 1 の近傍には、ホームニューロンとそれに隣接するニューロンが含まれます。直径 2 の近傍には、直径 1 のニューロンとそれに隣接するニューロンが含まれます。

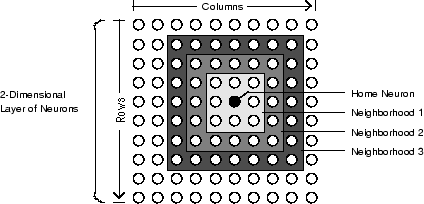
Graph showing a home neuron in a two-dimensional layer of neurons.

関数 dist では、S 個のニューロンから成る層マップに対するすべての近傍は、距離の S 行 S 列の行列で表されます。上記のような特定の距離 (隣接する近傍に対して 1、近傍 2 に対して 2 など) は、関数 boxdist によって生成されます。gridtop 構成に 6 個のニューロンがあるとします。

pos = gridtop([2, 3])
pos =
     0     1     0     1     0     1
     0     0     1     1     2     2

このとき、ボックス距離は次のようになります。

d = boxdist(pos)
d =
     0     1     1     1     2     2
     1     0     1     1     2     2
     1     1     0     1     1     1
     1     1     1     0     1     1
     2     2     1     1     0     1
     2     2     1     1     1     0

ニューロン 1 から 2、3、4 までの距離は、これらが隣接する近傍にあるため 1 になります。ニューロン 1 から 5 と 6 までの距離はどちらも 2 です。3 と 4 の両方から他のすべてのニューロンまでの距離はわずか 1 です。

あるニューロンからの "リンク距離" は、考慮するニューロンに到達するために必要なリンク数、つまりステップ数になります。そのため、linkdist を使用して同じニューロンのセットの距離を計算すると、次のようになります。

dlink =
     0     1     1     2     2     3
     1     0     2     1     3     2
     1     2     0     1     1     2
     2     1     1     0     2     1
     2     3     1     2     0     1
     3     2     2     1     1     0

2 つのベクトル x と y の間のマンハッタン距離は次のように計算されます。

D = sum(abs(x-y))

そのため、

W1 = [1 2; 3 4; 5 6]
W1 =
     1     2
     3     4
     5     6

と

P1 = [1;1]
P1 =
     1
     1

について、距離は次のようになります。

Z1 = mandist(W1,P1)
Z1 =
     1
     5
     9

mandist によって計算された距離は、確かに上記の数式に従っています。

アーキテクチャ

この SOFM のアーキテクチャは以下のとおりです。

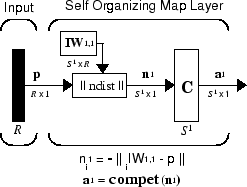
Schematic of a Self Organizing Feature Map Network, where input vector p is passed to a competitive layer that calculates output a.

このアーキテクチャは競合ネットワークと似ていますが、バイアスを使用していない点で異なります。競合伝達関数は、勝者ニューロン i* に対応する出力要素 a¹_i に対して、1 を生成します。a¹ の他のすべての出力要素は 0 です。

ただし、前述のとおり、勝者ニューロンに近いニューロンは、勝者ニューロンと共に更新されます。ニューロンのトポロジはさまざまなものを選択できます。同様に、勝者ニューロンに近いニューロンを計算するために、さまざまな距離の式を選択できます。

自己組織化マップニューラルネットワークの作成 (`selforgmap`)

新しい SOM ネットワークは関数 selforgmap を使用して作成できます。この関数は 2 つの学習フェーズで使用する変数を定義します。

順序付けフェーズの学習率
順序付けフェーズのステップ数
調整フェーズの学習率
調整フェーズの近傍距離

これらの値は、学習と適応に使用されます。

次の例を考えます。

2 つの要素から成る入力ベクトルを持つネットワークを作成し、2 行 3 列の六角形ネットワークに 6 個のニューロンがあるようにするとします。このネットワークを得るためのコードは次のとおりです。

net = selforgmap([2 3]);

学習するベクトルは次のとおりとします。

P = [.1 .3 1.2 1.1 1.8 1.7 .1 .3 1.2 1.1 1.8 1.7;...
0.2 0.1 0.3 0.1 0.3 0.2 1.8 1.8 1.9 1.9 1.7 1.8];

次を使用して、ネットワークを構成し、データを入力してこのすべてをプロットできます。

net = configure(net,P);
plotsompos(net,P)

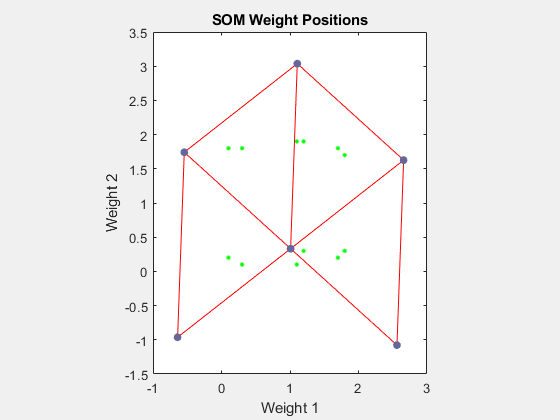
Figure SOM Weight Positions (plotsompos) contains an axes object. The axes object with title SOM Weight Positions, xlabel Weight 1, ylabel Weight 2 contains 3 objects of type line. One or more of the lines displays its values using only markers

緑色の点は学習ベクトルです。selforgmap の初期化によって、初期重みが入力空間に広がります。これらは最初、学習ベクトルから少し離れていることに注意してください。

ネットワークをシミュレーションするときに、各ニューロンの重みベクトルと入力ベクトルとの間の負の距離が計算され (negdist)、重み付けされた入力が求められます。重み付けされた入力は、正味入力 (netsum) でもあります。正味入力は競合 (compet) し、最も大きい正の正味入力を持つニューロンのみが 1 を出力します。

学習 (`learnsomb`)

自己組織化特徴マップの既定の学習は、バッチモード (trainbu) で行われます。自己組織化マップの重み学習関数は learnsomb です。

最初に、ネットワークは各入力ベクトルに対する勝者ニューロンを識別します。その後、各重みベクトルは、自身が勝者であるか、勝者の近傍にあるような入力ベクトルすべての平均位置の方向に移動します。近傍のサイズを定義する距離は、2 つのフェーズを通じて学習中に変更されます。

順序付けフェーズ

このフェーズは、指定したステップ数だけ行われます。近傍距離は、指定された初期距離から始まり、調整近傍距離 (1.0) まで減少します。このフェーズで近傍距離が減少するのに伴い、ネットワークのニューロンは通常、物理的な順序付けと同じトポロジを使用して、入力空間で自分自身の順序付けを行います。

調整フェーズ

このフェーズは、学習または適応の後に行われます。近傍サイズは 1 未満に減少します。そのため、各標本の勝者ニューロンの学習だけが行われます。

これらのネットワークでよく使用される特定の値をいくつか見てみましょう。

学習は learnsomb の学習パラメーター (以下に既定値を示す) に従って行われます。

学習パラメーター	既定値	目的
`LP.init_neighborhood`	`3`	初期近傍サイズ
`LP.steps`	`100`	順序付けフェーズのステップ数

近傍サイズ NS は、順序付けフェーズと調整フェーズの 2 つのフェーズを通じて変更されます。

順序付けフェーズは、ステップ数 LP.steps だけ行われます。このフェーズの間、アルゴリズムによって ND が初期近傍サイズ LP.init_neighborhood から 1 まで調整されます。このフェーズの間に、ニューロンの重みが、関連するニューロンの位置と一致するように入力空間に順序付けられます。

調整フェーズの間は、ND は 1 未満です。このフェーズの間に、順序付けフェーズで求められたトポロジカル順序を保持しながら、重みが入力空間に比較的均等に広がることが期待されます。

つまり、ニューロンの重みベクトルは最初、入力空間の中で入力ベクトルが存在する領域の方向にいっせいに大きいステップで移動します。それから近傍サイズが 1 まで減少するにつれて、マップは与えられた入力ベクトルに対してトポロジカルに順序付けられるようになります。近傍サイズが 1 になると、ネットワークはかなり適切に順序付けられています。学習は、ニューロンが入力ベクトル全体に均等に広がるまで続けられます。

競合層と同様に、自己組織化マップのニューロンは、入力空間のセクション全体で均等な確率で入力ベクトルが提示された場合、それらの間隔がほぼ等しい距離になるように順序付けられます。また、入力ベクトルが入力空間全体で異なる頻度で提示された場合、特徴マップの層のニューロンは、その層の入力ベクトルの頻度に比例するように領域に割り当てられます。

したがって、特徴マップは入力を分類するように学習が行われる一方で、入力のトポロジと分布の両方も学習します。

次を使用して、ネットワークの学習を 1000 エポック行うことができます。

net.trainParam.epochs = 1000;
net = train(net,P);

Figure Neural Network Training (03-Mar-2023 09:05:30) contains an object of type uigridlayout.

plotsompos(net,P)

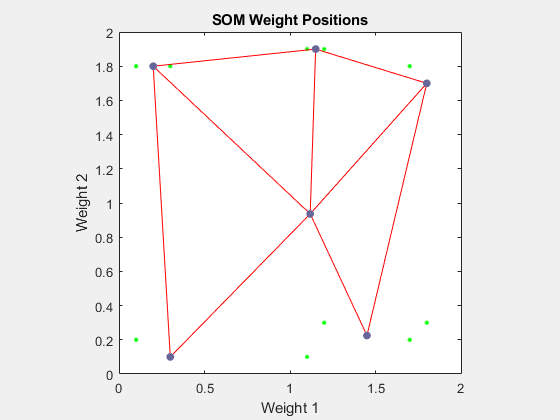
ニューロンがさまざまな学習グループの方向に移動を始めることがわかります。ニューロンが各グループにもっと近づくには、さらに学習が必要です。

前述のように、自己組織化マップは、ニューロンが重みを更新する点で従来の競合学習とは異なります。特徴マップでは、勝者のみが更新される代わりに、勝者とその近傍の重みが更新されます。結果として、近傍ニューロンが類似の重みベクトルを持ち、類似の入力ベクトルに対して応答するようになります。

例

以下に 2 つの例を簡単に示します。同様の例1 次元自己組織化マップと2 次元自己組織化マップも試してみてください。

1 次元自己組織化マップ

0°と 90°の間に均等に分布する 100 個の 2 要素単位入力ベクトルを考えます。

angles = 0:0.5*pi/99:0.5*pi;

以下はこのデータのプロットです。

P = [sin(angles); cos(angles)];

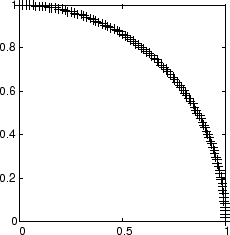
Plot of 100 unit vectors spread evenly between 0 degrees and 90 degrees.

自己組織化マップは 10 個のニューロンから成る 1 次元層として定義されます。このマップは、上で示したこれらの入力ベクトルについて学習が行われます。当初、これらのニューロンは図の中央にあります。

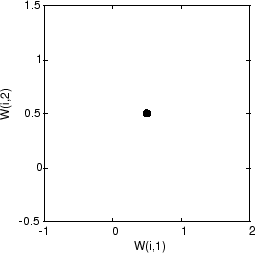
Plot of the weight vectors before training, showing a single point.

もちろん、すべての重みベクトルが入力ベクトル空間の中央から始まるので、現在は 1 つの円に見えます。

学習を開始すると、重みベクトルは、入力ベクトルの方向にいっせいに移動します。これらは、近傍サイズが減少するにつれて、順序付けられていきます。最終的に、層の重みが調整され、各ニューロンが多くの入力ベクトルによって占められている入力空間の領域に強く応答するようになります。近傍ニューロンの重みベクトルの配置には、入力ベクトルのトポロジも反映されています。

Plot of the weight vectors after training, showing the weight vectors lying on the boundary of the unit circle, mirroring the input vectors.

自己組織化マップは、入力ベクトルがランダムな順序で使用されて学習が行われるので、同じ初期ベクトルで開始しても学習の結果が必ず同じになるわけではないことに注意してください。

2 次元自己組織化マップ

この例では、2 次元自己組織化マップの学習方法を示します。

最初に、次のコードでランダムな入力データが作成されます。

P = rands(2,1000);

以下はこれらの 1000 個の入力ベクトルのプロットです。

Plot of 1000 random input vectors between [-1 -1] and [1 1].

これらの入力ベクトルを分類するために、30 個のニューロンから成る 5 x 6 の 2 次元マップが使用されます。2 次元マップは、5 x 6 個のニューロンで、マンハッタン距離近傍関数 mandist に従って距離が計算されます。

その後、20 サイクルごとに表示しながら、5000 提示サイクルにわたってマップの学習が行われます。

以下は 40 サイクル後の自己組織化マップです。

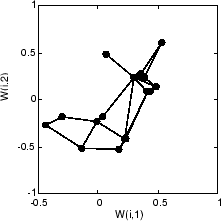
Plot of weight vectors after 40 cycles.

円で示されている重みベクトルは、ほぼランダムに配置されています。しかし、わずか 40 サイクル後に、線で結ばれている近傍ニューロンの重みベクトルは互いに近くなっています。

以下は 120 サイクル後のマップです。

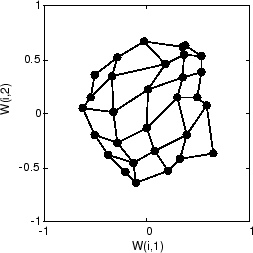
Plot of weight vectors after 120 cycles.

120 サイクル後には、入力ベクトルを制約する入力空間のトポロジに従って、マップの組織化が始まっています。

500 サイクル後の以下のプロットは、マップが入力空間全体にわたってさらに均等に分布していることを示しています。

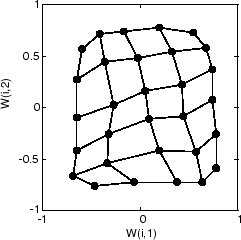
Plot of weight vectors after 500 cycles.

最終的に、5000 サイクル後に、マップは入力空間全体にかなり均等に広がります。さらに、ニューロンは、この問題における入力ベクトルの均等な分布を反映して、非常に均等に配置されます。

Plot of weight vectors after 5000 cycles.

このように 2 次元自己組織化マップは、入力空間のトポロジを学習します。

自己組織化マップが、近傍ニューロンが類似の入力を認識するように組織化されるまでにそれほど時間を要さないのに対して、入力ベクトルの分布に従って最終的に配置されるまでには時間を要することに注意してください。

バッチアルゴリズムを使用した学習

バッチ学習アルゴリズムは、一般的にインクリメンタルアルゴリズムよりもはるかに高速であり、SOFM 学習の既定アルゴリズムになっています。以下のコマンドを使用して、単純なデータセットに対してこのアルゴリズムの実験を行えます。

x = simplecluster_dataset
net = selforgmap([6 6]);
net = train(net,x);

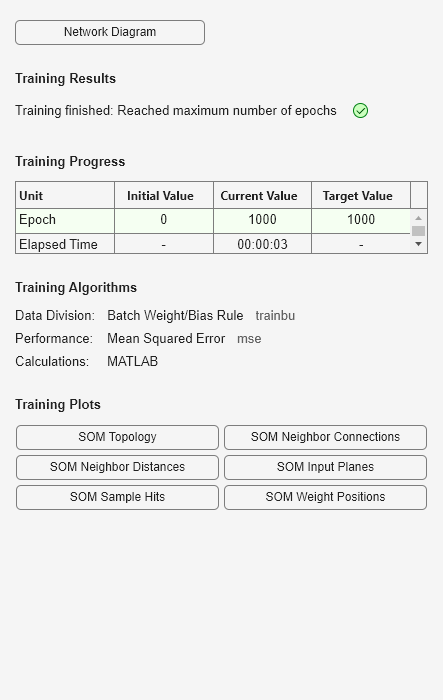
このコマンドシーケンスでは、36 個のニューロンから成る 6 x 6 の 2 次元マップが作成され、学習が行われます。学習中は、次の図が表示されます。

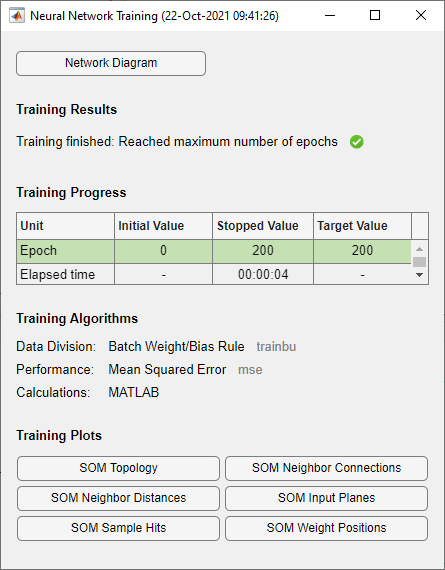
Neural Network Training Progress Window, showing that the network trained for 200 epochs in 4 seconds.

このウィンドウから、さまざまな便利な可視化にアクセスできます。[SOM Weight Positions] をクリックすると、データ点と重みベクトルの位置を示す次の図が表示されます。図が示しているように、バッチアルゴリズムをわずか 200 回反復しただけで、マップは入力空間にうまく分布しています。

Plot of the data points and weight vectors, with the 36 weight vectors arranged according to the distribution of input data points.

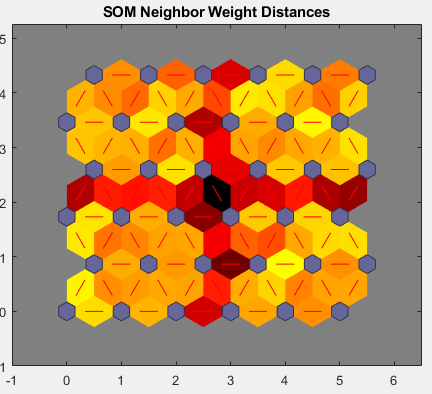
入力空間の次元数が多い場合は、すべての重みを一度に可視化することはできません。この場合、[SOM Neighbor Distances] をクリックします。近傍ニューロン間の距離を示す次の図が表示されます。

この図は、次の色分けを使用しています。

青い六角形はニューロンを表す。
赤線は近傍ニューロンを結合する。
赤線を含む領域内の色はニューロン間の距離を示す。
色が濃いほど、距離が遠いことを表す。
色が薄いほど、距離が近いことを表す

薄い色のセグメントから成る 4 つのグループが表示され、濃い色のセグメントと境界が接しています。このグループ化は、ネットワークがデータを 4 つのグループにクラスター化したことを示します。これら 4 つのグループは、前の重み位置の図でも確認できます。

Neighbour distances plot.

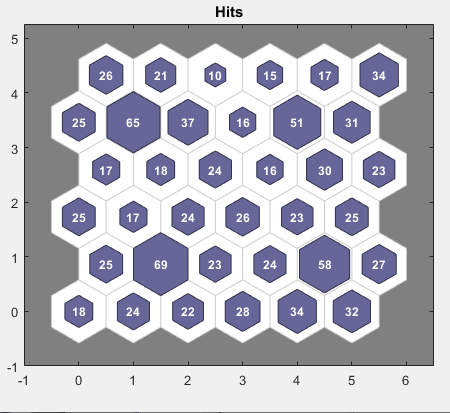
もう 1 つの便利な図では、各ニューロンに関連付けられたデータ点の数を確認できます。[SOM Sample Hits] をクリックして次の図を表示します。データがニューロン全体に非常に均等に分布していれば理想的です。この例では、データは隅にあるニューロンに少し集中していますが、全体の分布は非常に均等です。

Sample hits plot showing how many data points are associated with each neuron by plotting 36 hexagons representing the neurons, each with a number overlaid indicating how many data points are associated with that neuron.

重み平面の図を使用すると、重み自体も可視化できます。学習ウィンドウで [SOM 入力平面] をクリックして次の図を表示します。入力ベクトルの各要素 (この場合は 2 個) に対して 1 つずつ重み平面があります。これらは、各入力を各ニューロンに結合する重みを可視化したものです (薄い色と濃い色はそれぞれ大きな重みと小さな重みを表します)。2 つの入力の結合パターンが非常に似ている場合、入力に高い相関があると想定できます。この場合、入力 1 の結合は、入力 2 の結合とは非常に異なっています。

Weight planes plots, showing two weights planes that appear different indicating that the inputs are not highly correlated.