多項式モデル

多項式モデルについて

曲線の多項式モデルは次で与えられます

$y = \sum_{i = 1}^{n + 1} p_{i} x^{n + 1 - i}$

ここで、n + 1 は多項式の "位数"、n は多項式の "次数" であり、1 ≤ n ≤ 9 です。位数は近似される係数の数、次数は予測子変数の最大のべき乗数です。

このガイドでは、多項式はその次数に着目して記述します。たとえば、3 次多項式は次で与えられます

$γ = p_{1} x^{3} + p_{2} x^{2} + p_{3} x + p_{4}$

簡単な経験的モデルが必要な場合、通常は多項式が使用されます。多項式モデルを使用すると内挿または外挿を実行でき、またグローバル近似によりデータを特徴付けることもできます。たとえば、J 型熱電対の 0 から 760 度の温度範囲における温度から電圧への変換は、7 次多項式で記述されます。

メモ:

グローバルなパラメトリック近似は必要なく、できるだけ柔軟な近似が必要な場合は、区分的多項式が最適な手法である可能性があります。詳細については、ノンパラメトリック近似を参照してください。

多項式近似の主な利点に、あまり複雑でないデータへの妥当な柔軟性、および線形であることによる近似プロセスの単純さがあります。主な欠点は、高次近似が不安定になる場合があることです。また、どの次数の多項式もデータ範囲内では適切な近似を与えますが、その範囲の外では大きなずれが生じる可能性があります。そのため、多項式による外挿を行うときは注意が必要です。

高次多項式を使用して近似する場合、近似手順では非常に大きな値を含む行列の基底として予測子の値を使用するため、スケーリングの問題が発生することがあります。これに対処するには、データをゼロ平均にセンタリングし単位標準偏差にスケーリングすることにより、データを正規化する必要があります。データを正規化するには、曲線フィッターアプリで [データのセンタリングとスケーリング] チェックボックスをオンにします。

多項式モデルによる対話的な近似

MATLAB^® コマンドラインで curveFitter と入力して曲線フィッターアプリを開きます。または、[アプリ] タブの [数学、統計および最適化] グループで [曲線フィッター] をクリックします。
曲線フィッターアプリで曲線または曲面のデータを選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。ダイアログボックスでデータ変数を選択します。
- 曲線データ ([X データ] と [Y データ]、またはインデックスに対する [Y データ] のみ) を選択すると、既定の曲線近似が作成されます (既定の曲線近似は [多項式] 近似です)。
- 曲面データ ([X データ]、[Y データ]、[Z データ]) を選択すると、既定の曲面近似が作成されます (既定の曲面近似は [内挿] 近似です)。[近似タイプ] セクションの矢印をクリックしてギャラリーを開き、[回帰モデル] グループの [多項式] をクリックします。

曲線データの場合は、X の [多項式] 近似が作成されます。

Fit Options pane for curve data polynomial fit

曲面データの場合は、X および Y の [多項式] 近似が作成されます。

Fit Options pane for surface data polynomial fit

[近似オプション] ペインで、次のオプションを指定できます。

変数 X および変数 Y の次数:
- 曲線データの場合、X の次数は 9 までです。
- 曲面データの場合、X と Y の次数は 5 までです。[多項式] 近似の次数は、X および Y の次数がその上限です。詳細については、多項式曲面近似における多項式の項の定義を参照してください。
使用するロバスト線形最小二乗近似法 (Off、LAR または Bisquare)。詳細については、関数 fitoptions の名前と値の引数 Robust を参照してください。
範囲の設定や項の除外を行います。範囲を 0 に設定すると任意の項を除外できます。[結果] ペインを参照し、モデル項、係数の値、適合度の統計量を確認します。

ヒント

データ変数間のスケールが大きく異なる場合は、[データのセンタリングとスケーリング] チェックボックスがオンの場合とオフの場合とで近似の違いを確認してください。データのスケーリングにより近似を改善できる可能性がある場合は、[結果] ペインにメッセージが表示されます。

さまざまな多項式近似を比較する例については、曲線フィッターアプリにおける近似の比較を参照してください。

関数 fit による多項式近似

スクリプトを開く

この例では、関数 fit を使用して多項式によりデータを近似する方法を示します。この手順では、多項式曲線や多項式曲面による近似とプロット、近似オプションの指定、適合度の統計量の確認、予測の計算、信頼区間の表示を行います。

多項式ライブラリモデルは、関数 fit および fittype の入力引数です。モデルタイプを poly の末尾に x の次数 (最大 9) または x と y の次数 (最大 5) を付けて指定します。たとえば、'poly2' で 2 次曲線、または 'poly33' で 3 次曲面を指定します。

2 次多項式曲線の作成とプロット

データを読み込み、2 次多項式で近似します。文字列 'poly2' で 2 次多項式を指定します。

load census;
fitpoly2=fit(cdate,pop,'poly2')
% Plot the fit with the plot method.
plot(fitpoly2,cdate,pop)
% Move the legend to the top left corner.
legend('Location','NorthWest' );

fitpoly2 = 

     Linear model Poly2:
     fitpoly2(x) = p1*x^2 + p2*x + p3
     Coefficients (with 95% confidence bounds):
       p1 =    0.006541  (0.006124, 0.006958)
       p2 =      -23.51  (-25.09, -21.93)
       p3 =   2.113e+04  (1.964e+04, 2.262e+04)

3 次曲線の作成

3 次多項式 'poly3' で近似します。

fitpoly3=fit(cdate,pop,'poly3')
plot(fitpoly3,cdate,pop)

Warning: Equation is badly conditioned. Remove repeated data points or try
centering and scaling. 

fitpoly3 = 

     Linear model Poly3:
     fitpoly3(x) = p1*x^3 + p2*x^2 + p3*x + p4
     Coefficients (with 95% confidence bounds):
       p1 =   3.855e-06  (-4.078e-06, 1.179e-05)
       p2 =    -0.01532  (-0.06031, 0.02967)
       p3 =       17.78  (-67.2, 102.8)
       p4 =       -4852  (-5.834e+04, 4.863e+04)

近似オプションの指定

3 次近似の場合、方程式が悪条件であることを示す警告が表示されるため、'Normalize' オプションを指定してセンタリングとスケーリングを試みる必要があります。データのセンタリングとスケーリング、ロバスト近似オプションを両方指定して 3 次多項式で近似します。ロバストの 'on' によって、ロバスト線形最小二乗近似法の既定の方法 'Bisquare' 相当が簡便に設定されます。

fit3=fit(cdate, pop,'poly3','Normalize','on','Robust','on')
plot(fit3,cdate,pop)

fit3 = 

     Linear model Poly3:
     fit3(x) = p1*x^3 + p2*x^2 + p3*x + p4
       where x is normalized by mean 1890 and std 62.05
     Coefficients (with 95% confidence bounds):
       p1 =     -0.4619  (-1.895, 0.9707)
       p2 =       25.01  (23.79, 26.22)
       p3 =       77.03  (74.37, 79.7)
       p4 =       62.81  (61.26, 64.37)

ライブラリモデルの 'poly3' に設定できるパラメーターを確認するには、関数 fitoptions を使用します。

fitoptions poly3

ans = 

  llsqoptions with properties:

        Lower: []
        Upper: []
       Robust: 'Off'
    Normalize: 'off'
      Exclude: []
      Weights: []
       Method: 'LinearLeastSquares'

適合度の統計量の取得

3 次多項式の適合度の統計量を取得するには 'gof' 出力引数を指定します。

[fit4, gof]=fit(cdate, pop,'poly3','Normalize','on');
gof

gof = 

  struct with fields:

           sse: 149.7687
       rsquare: 0.9988
           dfe: 17
    adjrsquare: 0.9986
          rmse: 2.9682

残差のプロットによる近似の評価

残差をプロットするには、plot メソッドにプロットタイプとして 'residuals' を指定します。

plot(fit4,cdate, pop,'residuals');

データ範囲外の近似の検証

既定の設定では、近似はデータの範囲全体についてプロットされます。別の範囲で近似をプロットするには、近似をプロットする前に x 軸範囲を設定します。たとえば、近似から外挿された値を確認するには、x 軸範囲の上限を 2050 に設定します。

plot( cdate, pop, 'o' );
xlim( [1900, 2050] );
hold on
plot( fit4 );
hold off

予測限界のプロット

予測限界をプロットするには、プロットタイプとして 'predobs' または 'predfun' を使用します。

plot(fit4,cdate,pop,'predobs')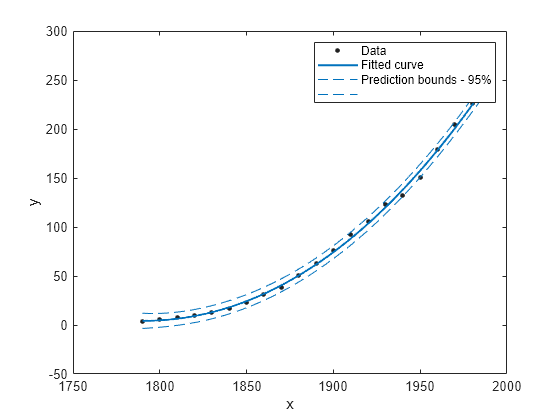

3 次多項式の予測限界を 2050 年までプロットします。

plot( cdate, pop, 'o' );
xlim( [1900, 2050] )
hold on
plot( fit4, 'predobs' );
hold off

新しいクエリ点での信頼限界の取得

いくつかの新しいクエリ点で近似を評価します。

cdateFuture = (2000:10:2020).';
popFuture = fit4( cdateFuture )

popFuture =

  276.9632
  305.4420
  335.5066

predint メソッドを使用し、将来の人口の予測について 95% 信頼限界を計算します。

ci = predint( fit4, cdateFuture, 0.95, 'observation' )

ci =

  267.8589  286.0674
  294.3070  316.5770
  321.5924  349.4208

近似とデータに対して、予測された将来の人口を信頼区間と共にプロットします。

plot(cdate, pop, 'o');
xlim([1900, 2040])
hold on
plot(fit4)
h = errorbar(cdateFuture,popFuture,popFuture-ci(:,1),ci(:,2)-popFuture,'.');
hold off
legend('cdate v pop','poly3','prediction','Location','NorthWest')

多項式曲面の近似とプロット

曲面データを読み込み、x と y の 4 次多項式で近似します。

load franke;
fitsurface=fit([x,y],z, 'poly44','Normalize','on')
plot(fitsurface, [x,y],z)

fitsurface = 

     Linear model Poly44:
     fitsurface(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3 
                    + p21*x^2*y + p12*x*y^2 + p03*y^3 + p40*x^4 + p31*x^3*y 
                    + p22*x^2*y^2 + p13*x*y^3 + p04*y^4
       where x is normalized by mean 1982 and std 868.6
       and where y is normalized by mean 0.4972 and std 0.2897
     Coefficients (with 95% confidence bounds):
       p00 =      0.3471  (0.3033, 0.3909)
       p10 =     -0.1502  (-0.1935, -0.107)
       p01 =     -0.4203  (-0.4637, -0.377)
       p20 =      0.2165  (0.1514, 0.2815)
       p11 =      0.1717  (0.1175, 0.2259)
       p02 =     0.03189  (-0.03351, 0.09729)
       p30 =     0.02778  (0.00749, 0.04806)
       p21 =     0.01501  (-0.002807, 0.03283)
       p12 =    -0.03659  (-0.05439, -0.01879)
       p03 =      0.1184  (0.09812, 0.1387)
       p40 =    -0.07661  (-0.09984, -0.05338)
       p31 =    -0.02487  (-0.04512, -0.004624)
       p22 =   0.0007464  (-0.01948, 0.02098)
       p13 =    -0.02962  (-0.04987, -0.009366)
       p04 =    -0.02399  (-0.0474, -0.0005797)

多項式モデルの近似オプション

すべての近似法に、既定のプロパティとして Normalize、Exclude、Weights および Method があります。例については、コマンドラインでの近似オプションの指定を参照してください。

多項式モデルには、Method プロパティの値として LinearLeastSquares があり、次の表に示す追加の近似オプションプロパティがあります。すべての近似オプションの詳細については、fitoptions のリファレンスページを参照してください。

プロパティ	説明
`Robust`	使用するロバスト線形最小二乗近似法を指定します。値は `'on'`、`'off'`、`'LAR'` または `'Bisquare'` です。既定の設定は `'off'` です。 `'LAR'` は最小絶対残差法を指定し、`'Bisquare'` は二重平方重み法を指定します。`'on'` は既定の方法である `'Bisquare'` と同等です。
`Lower`	近似される係数の下限のベクトル。既定値は空のベクトルであり、近似が下限によって制約されないことを示します。範囲を指定する場合、ベクトルの長さは係数の数と等しくなければなりません。個々の制約なしの下限は `-Inf` によって指定できます。
`Upper`	近似される係数の上限のベクトル。既定値は空のベクトルであり、近似が上限によって制約されないことを示します。範囲を指定する場合、ベクトルの長さは係数の数と等しくなければなりません。個々の制約なしの上限は `Inf` によって指定できます。

多項式曲面近似における多項式の項の定義

x および y 入力の次数を指定することにより、多項式曲面モデルに含まれる項を制御できます。i が x の次数で j が y の次数の場合、多項式全体の次数は i および j がその上限です。各項の x の次数は i 以下であり、各項の y の次数は j 以下です。i と j の最大値はどちらも 5 です。

以下に例を示します。

poly21  Z = p00 + p10*x + p01*y + p20*x^2 + p11*x*y

poly13  Z = p00 + p10*x + p01*y + p11*x*y + p02*y^2 
                      + p12*x*y^2 + p03*y^3

poly55  Z = p00 + p10*x + p01*y +...+ p14*x*y^4 
                      + p05*y^5

たとえば、x の次数を 3、y の次数を 2 に指定すると、モデル名は poly32 になります。モデル項は次の表のようになります。

項の次数	0	1	2
0	1	y	y²
1	x	xy	xy²
2	x²	x²y	該当なし
3	x³	該当なし	該当なし

多項式全体の次数は i および j の上限は超えられません。この例で、x³y や x²y² などの項は、次数の合計が 3 を上回るため除外されます。どちらの場合も、全次数は 4 です。