回転ディスクの制御設計

この例では次を使用します。

この例では、[1] に記載のある連動回転ディスクで構成される機械システムのゲインスケジュール $H_{2}$ コントローラーを設計する方法を示します。

連動回転ディスク

次の図に 1 対の回転ディスクを示します。スロットディスクは $Ω_{1}$ rad/s および $Ω_{2}$ rad/s の速度で回転します。ディスクの質量 $M_{1}$ および $M_{2}$ は、水平面上を半径方向にスライドして動きます。2 つの質量は、圧縮と引張の両方の力を伝えるワイヤ、カプラー、およびプーリから成るシステムで連結されます。この連結システムはバネ定数 $k$ のバネとして機能し、各質量の滑り運動による摩擦は減衰係数 $b$ でモデル化されます。

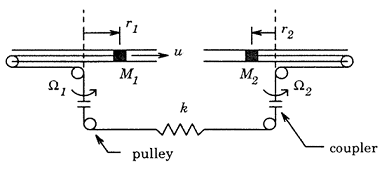
A pair of spinning disks.

目標は、2 つの質量の位置 (質量 $M_{1}$ の $r_{1}$ と $M_{2}$ の $r_{2}$ ) を制御することです。制御入力は質量 $M_{1}$ に作用する半径方向の力 $f_{u}$ で、各質量に半径方向の外乱力 $f_{1}$ および $f_{2}$ が作用します。運動方程式は次のとおりです。

$M_{1} (\ddot{r_{1}} - Ω_{1}^{2} r_{1}) + b \dot{r_{1}} + k (r_{1} + r_{2}) = f_{u} + f_{1}$

$M_{2} (\ddot{r_{2}} - Ω_{2}^{2} r_{2}) + b \dot{r_{2}} + k (r_{1} + r_{2}) = f_{2}$

ここで、以下となります。

$M_{1}$ = 1 kg です。これは、ディスク 1 のスライドする質量の大きさです。
$M_{1}$ = 2 kg です。これは、ディスク 2 のスライドする質量の大きさです。
$b$ = 1 kg/s です。これは、摩擦による減衰係数です。
$k$ = 200 N/m です。これは、質量を連結するシステムのバネ定数です。
$r_{1} (t)$ は、スライドする質量 $M_{1}$ のディスク 1 の中心からの位置 (m) です。
$r_{2} (t)$ は、スライドする質量 $M_{2}$ のディスク 2 の中心からの位置 (m) です。
$Ω_{1} (t)$ は、ディスク 1 の回転速度 (rad/s) です。
$Ω_{2} (t)$ は、ディスク 2 の回転速度 (rad/s) です。
$f_{u}$ は、質量 $M_{1}$ に対して半径方向に作用する制御力 (N) です。
$f_{1}$ と $f_{2}$ は、 $M_{1}$ と $M_{2}$ のそれぞれに対して半径方向に作用する外乱力 (N) です。

回転ディスクの回転速度は、範囲 $Ω_{1} \in [0, 3]$ および $Ω_{2} \in [0, 5]$ (rad/s) で変動します。これらの速度は事前にはわかりませんが、測定したものを制御設計に使用できます。制御設計の目的は、質量 $M_{2}$ の半径方向の位置を指示することです。制御入力は質量 $M_{1}$ に適用され、ディスク連結システムを通じて質量 $M_{2}$ に伝わることに注意してください。

LPV モデル

運動方程式は、速度 $Ω_{1}$ および $Ω_{2}$ 以外は線形です。スケジューリングパラメーターとして $p_{1} = Ω_{1}^{2}$ 、 $p_{2} = Ω_{2}^{2}$ 、 $p_{1} \in [0, 9]$ 、 $p_{2} \in [0, 25]$ を選択すると、システム全体の LPV モデルは次のようになります。

$\dot{x} (t) = [\begin{array}{c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ p_{1} - \frac{k}{M_{1}} & - \frac{k}{M_{1}} & - \frac{b}{M_{1}} & 0 \\ - \frac{k}{M_{2}} & p_{2} - \frac{k}{M_{2}} & 0 & - \frac{b}{M_{2}} \end{array}] x (t) + [\begin{array}{c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \frac{1}{M_{1}} & \frac{0.1}{M_{1}} & 0 \\ 0 & 0 & \frac{0.1}{M_{2}} \end{array}] [\begin{array}{c} f_{u} (t) \\ f_{1} (t) \\ f_{2} (t) \end{array}]$

$y (t) = [\begin{array}{c} 0 & 1 & 0 & 0 \end{array}] x (t)$

ここで、状態ベクトル $x (t) = [\begin{array}{c} r_{1} (t) \\ r_{2} (t) \\ \dot{r_{1}} (t) \\ \dot{r_{2}} (t) \end{array}]$ です。

この LPV モデルを作成するには、行列 $A$ 、 $B$ 、 $C$ を計算する関数 disksGFCN をスケジューリングパラメーター $p = [\begin{array}{c} p_{1} \\ p_{2} \end{array}]$ の関数として記述します。この関数のコードを確認するには、ファイル disksGFCN.m を参照するか、コマンドラインで「type disksGFCN」と入力します。

システムのパラメーターを定義します。

m1 = 1;
m2 = 0.5;
k = 200;
b = 1;

LPV システムを定義します。

fh = @(t,p) disksGFCN(t,p,m1,m2,k,b);
G = lpvss(["p1","p2"],fh);

ゲインスケジュール H2 制御設計

ゲインスケジュール $H_{2}$ 最適コントローラーを設計します。最初に、( ${Ω_{1}^{2}}_{}$ , $Ω_{2}^{2}$ ) 値のグリッドの各点における $H_{2}$ 最適コントローラーを設計します。固定の回転速度の場合、このようなコントローラーにより、重み付けされた相互接続に対する外乱 $d = [\begin{array}{c} f_{1} (t) \\ f_{2} (t) \end{array}]$ から誤差 $e$ への閉ループ $H_{2}$ ノルムが最小化されます。重みが適切に選択されるように、この相互接続で制御則の目的の $H_{2}$ 性能を定義します。コントローラーは、基準値 $r$ と測定値 $y$ を受け取り、指令値 $u_{c}$ を生成します。

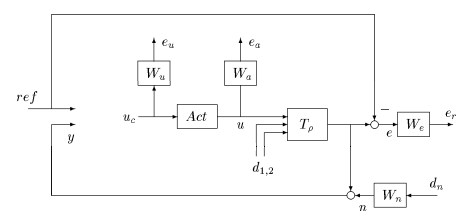
The weighted design interconnection.

重みを定義し、この相互接続の LPV モデルを作成します。

% Add input/output names to plant
G.InputName = {'u'; 'f1'; 'f2'};
G.OutputName = 'Gy';

% Actuator model
act = ss(-100,100,1,0);
act.InputName = 'uc';
act.OutputName = 'u';

% Weight: Control Command
Wu = ss(1/50);
Wu.InputName = 'uc';
Wu.OutputName = 'eu';

% Weight: Actuator Output
Wa = ss(0.00001);
Wa.InputName = 'u';
Wa.OutputName = 'ea';

% Weight: Tracking Error
We = tf(2,[1 0.04]);
We.InputName = 'e';
We.OutputName = 'er';

% Weight: Noise
Wn = tf([1,0.4],[0.01 400]);
Wn.InputName = 'dn';
Wn.OutputName = 'n';

% Form synthesis interconnection
sum1 = sumblk('y = Gy + n');
sum2 = sumblk('e = Gy - r');
IC = connect(G,act,Wu,Wa,We,Wn,sum1,sum2,{'r','f1','f2','dn','uc'},...
     {'eu','ea','er','r','y'});

( ${Ω_{1}^{2}}_{}$ , $Ω_{2}^{2}$ ) 値のグリッドを作成し、各グリッド点における $H_{2}$ 最適コントローラーを計算します。

p1 = linspace(0,9,3);
p2 = linspace(0,25,3);
[p1,p2] = ndgrid(p1,p2);

グリッド点の IC をサンプリングし、 $H_{2}$ 最適コントローラーを設計します。

nmeas = 2;   % # of measurements
ncon = 1;    % # of controls
ICs = sample(IC,[],p1,p2);
Ks = ss( zeros([ncon nmeas size(p1)]) );
for i=1:numel(p1)
   Ks(:,:,i) = h2syn(ICs(:,:,i),nmeas,ncon);
end

ssInterpolant を使用して、これらの $H_{2}$ コントローラーをグリッド点間に線形に内挿するゲインスケジュールコントローラーを作成します。この手法は、回転速度がゆっくり変化する場合に有効です。急激に変化する場合の LPV の代替方法については、[1] に記載されています。

Ks.SamplingGrid = struct('p1',p1,'p2',p2);
Klpv = ssInterpolant(Ks,[]);
Klpv.InputName = {'r','Gy'};
Klpv.OutputName = {'uc'};

LTI の性能の評価

制御設計よりも細かいグリッドを使用して、固定の回転速度についてゲインスケジュールコントローラーを評価します。

[r;f1;f2] から Gy への閉ループシステムを形成します。

CL = connect(G,act,Klpv,{'r','f1','f2'},{'Gy'});

より細かい点のグリッドで開ループと閉ループを評価します。

p1 = linspace(0,9,5);
p2 = linspace(0,25,5);
[p1,p2] = ndgrid(p1,p2);
Gs = sample(G,[],p1,p2);
CLs = sample(CL,[],p1,p2);

コントローラーは最小限のオーバーシュートで適切に追従しています。整定時間は約 2.5 秒で、定常状態の追従誤差は 3% 未満です。さらに、外乱の影響も最小限しかありません。

step(CLs,5)
grid on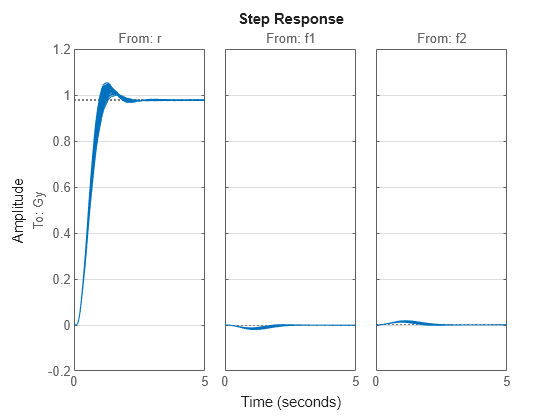

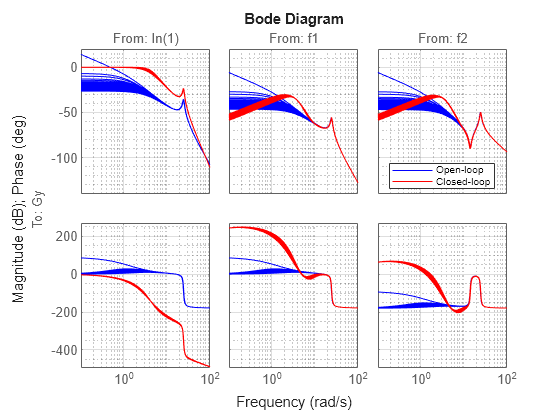
MATLAB figure

r から Gy への閉ループボード応答で、DC ゲインが帯域幅 3 rad/s 付近で 1 近くになっています。外乱抑制は 1 rad/s 未満で、開ループより適切です。

bode(Gs,"b",CLs,"r",{0.1,100})
legend("Open-loop","Closed-loop","Location","best")
grid minor

MATLAB figure

LPV の性能の評価

最後に、時変の回転速度を使用して時間領域シミュレーションでゲインスケジュールコントローラーを評価します。パラメーターは時間によって次のように変化します。

$p_{1} (t) = Ω_{1}^{2} (t) = \sin (t) + 1.5$ , $p_{2} (t) = Ω_{2}^{2} (t) = 0.5 \cos (5 t) + 3$ .

基準信号 $r$ は単位ステップで、外乱は次のように設定されます。

$f_{1} (t) = \cos (3 t) + \sin (5 t) + \cos (8 t)$ , $f_{2} (t) = \cos (t) + \sin (2 t) + \cos (4 t)$ .

システムへの入力を定義します。

t = 0:0.01:15;
u = ones(size(t));
d1 = cos(3*t)+sin(5*t)+cos(8*t);
d2 = cos(t)+sin(2*t)+cos(4*t);

パラメーターの軌跡を定義します。

p1 = sin(t)+1.5;
p2 = 0.5*cos(5*t)+3;

外乱がある場合とない場合について LPV モデルをシミュレートします。

[y1,t1,x1] = lsim(CL,[u;d1;d2],t,[],[p1;p2]);
[y2,t2,x2] = lsim(CL,[u;0*d1;0*d2],t,[],[p1;p2]);

figure 
plot(t1,y1,"b",t2,y2,"r");
grid on;
title("LPV Simulation")
ylabel("y");
legend("With disturbances","Without disturbances","Location","best")

Figure contains an axes object. The axes object with title LPV Simulation, ylabel y contains 2 objects of type line. These objects represent With disturbances, Without disturbances.

外乱による誤差は 5% ほどで、これは外乱なしの応答からの 1 ～ 2 Hz の振動に相当します。なお、この周波数範囲は、LTI の周波数応答解析で外乱が出力信号に最も影響していると示されている範囲です。

データ関数

type disksGFCN.m

function [A,B,C,D,E,dx0,x0,u0,y0,Delays] = GFCN(t,p,m1,m2,k,b)
% Matrices and offsets for LPV model of spinning disks.

% Enforce 0<=p1<=9, 0<=p2<=25
p(1) = max(0,min(p(1),9));
p(2) = max(0,min(p(2),25));

% Define state-space matrices
A = [   0              0            1       0    ; ...
        0              0            0       1    ; ...
    p(1)-k/m1       -k/m1        -b/m1     0    ; ...
      -k/m2         p(2)-k/m2       0     -b/m2  ];
B = [    0      0       0     ; ...
         0      0       0     ; ...
      1/m1   .1/m1      0     ; ...  
         0      0     .1/m2 ];
C = [ 0 1 0 0];
D = [0 0 0];
E = [];
% no offsets or delays
dx0 = []; x0 = []; u0 = []; y0 = []; Delays = [];

参考文献

[1] Wu, Fen. "Control of Linear Parameter Varying Systems," Ph.D. dissertation, Department of Mechanical Engineering, University of California at Berkeley, May 1995.

参考

lpvss | sample | ndgrid