LLR 推定用のニューラルネットワークの学習とテスト

この例では次を使用します。

この例では、厳密な対数尤度比 (LLR) の推定用に信号とチャネル劣化要因を生成して LLRNet というニューラルネットワークの学習を行う方法を示します。

5G New Radio (NR) や第 2 世代衛星デジタルビデオ放送規格 (DVB-S.2) などの最新の通信システムでは、軟復調ビット値を利用した前方誤り訂正アルゴリズムを使用しています。これらのシステムでは LLR の手法を使用して軟ビット値を計算します。LLR は、ビットが 0 である確率とビットが 1 である確率の比の対数と定義されます。以下で求められます。

$l_{i} ≜ \log (\frac{P_{r} (c_{i} = 0 | s_{}^{ˆ})}{P_{r} (c_{i} = 1 | s_{}^{ˆ})})$ , $i = 1, . . ., k$

ここで、 $s_{}^{ˆ}$ は k ビットの受信シンボル、 $c_{i}$ はシンボルの $i^{t h}$ 番目のビットです。加法性ホワイトガウスノイズ (AWGN) チャネルと仮定すると、厳密な LLR の式の計算は以下のとおりです。

$l_{i} ≜ \log (\frac{\sum_{s \in c_{i}^{0}} \exp (- \frac{‖ s_{}^{ˆ} - s ‖_{2}^{2}}{σ^{2}})}{\sum_{s \in c_{i}^{1}} \exp (- \frac{‖ s_{}^{ˆ} - s ‖_{2}^{2}}{σ^{2}})})$

ここで、 $σ^{2}$ はノイズ分散です。指数と対数の計算には、特に組み込みシステムでは非常にコストがかかります。そのため、ほとんどの実用的なシステムでは最大対数近似が使用されます。与えられた配列 $x$ について、最大対数近似は以下のとおりです。

$\log (\sum_{j} \exp (- x_{j}^{2})) \approx \max_{j} (- x_{j}^{2})$ .

これを厳密な LLR の式に代入すると、最大対数 LLR 近似は以下になります [1]。

$l_{i} \approx \frac{1}{σ^{2}} (\min_{s \in C_{i}^{1}} ‖ s_{}^{ˆ} - s ‖_{2}^{2} - \min_{s \in C_{i}^{0}} ‖ s_{}^{ˆ} - s ‖_{2}^{2})$ .

LLRNet では、ニューラルネットワークを使用し、特定の SNR 値のベースバンド複素数受信シンボルを考慮して厳密な LLR 値を推定します。隠れ層の少ない浅層ネットワークでも、近似 LLR アルゴリズムと複雑度が同等の厳密な LLR 値を推定できる可能性があります [1]。

M-ary QAM の厳密な LLR、最大対数近似 LLR、および LLRNet の比較

5G NR では M-ary QAM 変調が使用されます。この節では、16-QAM、64-QAM、および 256-QAM 変調の LLR 値の推定における LLRNet の正確性を調べます。M-ary QAM システムが AWGN チャネル条件で動作するものと仮定します。この仮定は、周波数選択性のチャネルでシンボルがイコライズされる場合にも有効です。ここでは、以下の 3 つのアルゴリズムで計算した LLR 値を示します。

厳密な LLR
最大対数近似 LLR
LLRNet

16-QAM の LLR 推定の性能

受信する可能性があるシンボルの 99.7% ( $\pm 3 σ$ ) をカバーするシンボル値の厳密な LLR と近似 LLR の値を計算します。AWGN と仮定すると、受信信号の 99.7% ( $\pm 3 σ$ ) が $[\max_{s \in C} (R e (s) + 3 σ) \min_{s \in C} (R e (s) - 3 σ)] + i [\max_{s \in C} (I m (s) + 3 σ) \min_{s \in C} (I m (s) - 3 σ)]$ の範囲に含まれます。この空間に一様分布する I/Q シンボルを生成し、関数qamdemodを使用して厳密な LLR と近似 LLR の値を計算します。

M = 16;             % Modulation order
k = log2(M);        % Bits per symbols
SNRValues = -5:5:5; % in dB
numSymbols = 1e4;
numSNRValues = length(SNRValues);
symOrder = llrnetQAMSymbolMapping(M);

const = qammod(0:15,M,symOrder,'UnitAveragePower',1);
maxConstReal = max(real(const));
maxConstImag = max(imag(const));

numBits = numSymbols*k;
exactLLR = zeros(numBits,numSNRValues);
approxLLR = zeros(numBits,numSNRValues);
rxSym = zeros(numSymbols,numSNRValues);
for snrIdx = 1:numSNRValues
    SNR = SNRValues(snrIdx);
    noiseVariance = 10^(-SNR/10);
    sigma = sqrt(noiseVariance);
    
    maxReal = maxConstReal + 3*sigma;
    minReal = -maxReal;
    maxImag = maxConstImag + 3*sigma;
    minImag = -maxImag;
    
    r = (rand(numSymbols,1)*(maxReal-minReal)+minReal) + ...
        1i*(rand(numSymbols,1)*(maxImag-minImag)+minImag);
    rxSym(:,snrIdx) = r;
    
    exactLLR(:,snrIdx) = qamdemod(r,M,symOrder,...
        'UnitAveragePower',1,'OutputType','llr','NoiseVariance',noiseVariance);
    approxLLR(:,snrIdx) = qamdemod(r,M,symOrder,...
        'UnitAveragePower',1,'OutputType','approxllr','NoiseVariance',noiseVariance);
end

ニューラルネットワークの設定と学習

1 つの入力層、1 つの隠れ層、および 1 つの出力層を含む浅層ニューラルネットワークを設定します。受信シンボルをネットワークに入力し、学習を行って厳密な LLR 値を推定します。このネットワークでは実数入力を想定しているため、2 列のベクトルを作成し、1 列目を受信シンボルの実数値、2 列目を受信シンボルの虚数値とします。また、出力は $k \times N$ のベクトルでなければなりません。 $k$ はシンボルあたりのビット数、 $N$ はシンボル数です。

nnInput = zeros(numSymbols,2,numSNRValues);
nnOutput = zeros(numSymbols,k,numSNRValues);
for snrIdx = 1:numSNRValues
    rxTemp = rxSym(:,snrIdx);
    rxTemp = [real(rxTemp) imag(rxTemp)];
    nnInput(:,:,snrIdx) = rxTemp;
    
    llrTemp = exactLLR(:,snrIdx);
    nnOutput(:,:,snrIdx) = reshape(llrTemp, k, numSymbols)';
end

16-QAM シンボルの場合、隠れ層は 8 ニューロン、出力層は 4 ニューロンです。これはシンボルあたりのビット数に相当します。関数 llrnetNeuralNetwork は、事前構成されたニューラルネットワークを返します。このニューラルネットワークに 3 つの異なる SNR 値について学習させます。関数 qamdemod を使用して計算した厳密な LLR 値を、想定される出力値として使用します。

hiddenLayerSize = 8;
trainedNetworks = cell(1,numSNRValues);
for snrIdx=1:numSNRValues
    fprintf('Training neural network for SNR = %1.1fdB\n', ...
        SNRValues(snrIdx))
    x = nnInput(:,:,snrIdx)';
    y = nnOutput(:,:,snrIdx)';
    
    MSExactLLR = mean(y(:).^2);
    fprintf('\tMean Square LLR = %1.2f\n', MSExactLLR)
    
    % Train the Network. Use parallel pool, if available. Train three times
    % and pick the best one.
    mse = inf;
    for p=1:3
        netTemp = llrnetNeuralNetwork(hiddenLayerSize);
        if parallelComputingLicenseExists()
            [netTemp,tr] = train(netTemp,x,y,'useParallel','yes');
        else
            [netTemp,tr] = train(netTemp,x,y);
        end
        % Test the Network
        predictedLLRSNR = netTemp(x);
        mseTemp = perform(netTemp,y,predictedLLRSNR);
        fprintf('\t\tTrial %d: MSE = %1.2e\n', p, mseTemp)
        if mse > mseTemp
            mse = mseTemp;
            net = netTemp;
        end
    end
    
    % Store the trained network
    trainedNetworks{snrIdx} = net;
    fprintf('\tBest MSE = %1.2e\n', mse)
end

Training neural network for SNR = -5.0dB

	Mean Square LLR = 4.43

		Trial 1: MSE = 7.44e-05
		Trial 2: MSE = 6.90e-05
		Trial 3: MSE = 6.81e-05

	Best MSE = 6.81e-05

Training neural network for SNR = 0.0dB

	Mean Square LLR = 15.74

		Trial 1: MSE = 1.86e-03
		Trial 2: MSE = 4.04e-04
		Trial 3: MSE = 9.05e-05

	Best MSE = 9.05e-05

Training neural network for SNR = 5.0dB

	Mean Square LLR = 60.01

		Trial 1: MSE = 8.59e-03
		Trial 2: MSE = 2.19e-02
		Trial 3: MSE = 2.14e-02

	Best MSE = 8.59e-03

このネットワークの性能判定基準は平均二乗誤差 (MSE) です。最終的な MSE 値が示しているように、ニューラルネットワークは厳密な LLR の平均二乗値より少なくとも 40 dB 小さい MSE 値に収束します。SNR が増加すれば LLR 値も増加し、相対的に MSE 値が高くなることに注意してください。

16-QAM の結果

LLRNet の LLR の推定値を厳密な LLR および近似 LLR の推定値と比較します。1e4 の 16-QAM シンボルをシミュレートし、3 つのすべての手法を使用して LLR 値を計算します。前の節で生成したシンボルは使用しないでください。それらのシンボルを使用して LLRNet の学習を行ったため、LLRNet に不当に有利になることを避けるためです。

numBits = numSymbols*k;
d = randi([0 1], numBits, 1);

txSym = qammod(d,M,symOrder,'InputType','bit','UnitAveragePower',1);

exactLLR = zeros(numBits,numSNRValues);
approxLLR = zeros(numBits,numSNRValues);
predictedLLR = zeros(numBits,numSNRValues);
rxSym = zeros(length(txSym),numSNRValues);
for snrIdx = 1:numSNRValues
    SNR = SNRValues(snrIdx);
    sigmas = 10^(-SNR/10);
    r = awgn(txSym,SNR);
    rxSym(:,snrIdx) = r;
    
    exactLLR(:,snrIdx) = qamdemod(r,M,symOrder,...
        'UnitAveragePower',1,'OutputType','llr','NoiseVariance',sigmas);
    approxLLR(:,snrIdx) = qamdemod(r,M,symOrder,...
        'UnitAveragePower',1,'OutputType','approxllr','NoiseVariance',sigmas);
    
    net = trainedNetworks{snrIdx};
    x = [real(r) imag(r)]';
    tempLLR = net(x);
    predictedLLR(:,snrIdx) = reshape(tempLLR, numBits, 1);
end

qam16Results.exactLLR = exactLLR;
qam16Results.approxLLR = approxLLR;
qam16Results.predictedLLR = predictedLLR;
qam16Results.RxSymbols = rxSym;
qam16Results.M = M;
qam16Results.SNRValues = SNRValues;
qam16Results.HiddenLayerSize = hiddenLayerSize;
qam16Results.NumSymbols = numSymbols;

次の図は、厳密な LLR、最大対数近似 LLR、および LLRNet で推定した LLR 値と奇数ビットの受信シンボルの実数部を示したものです。LLRNet は SNR 値が低い場合でも厳密な LLR 値と一致しています。

llrnetPlotLLR(qam16Results,'16-QAM LLR Comparison')

64-QAM と 256-QAM の LLR 推定の性能

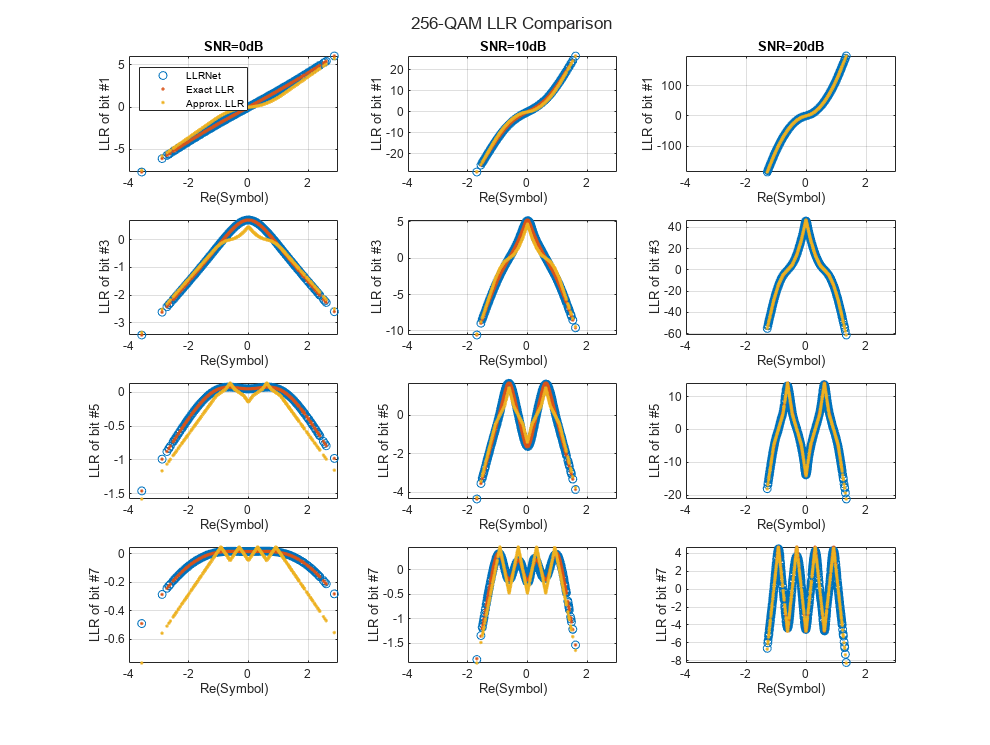
より高い次数の QAM についても LLRNet で LLR 値を推定できるか確認します。64-QAM および 256-QAM について、補助関数 llrnetQAMLLR を使用して 16-QAM と同じプロセスを繰り返します。次の図は、厳密な LLR、最大対数近似 LLR、および LLRNet で推定した LLR 値と奇数ビットの受信シンボルの実数部を示したものです。

trainNow = false;
if trainNow
    % Parameters for 64-QAM
    simParams(1).M = 64; %#ok<UNRCH>
    simParams(1).SNRValues = 0:5:10;
    simParams(1).HiddenLayerSize = 16;
    simParams(1).NumSymbols = 1e4;
    simParams(1).UseReLU = false;
    
    % Parameters for 256-QAM
    simParams(2).M = 256;
    simParams(2).SNRValues = 0:10:20;
    simParams(2).HiddenLayerSize = 32;
    simParams(2).NumSymbols = 1e4;
    simParams(2).UseReLU = false;
    
    simResults = llrnetQAMLLR(simParams);
    llrnetPlotLLR(simResults(1),sprintf('%d-QAM LLR Comparison',simResults(1).M))
    llrnetPlotLLR(simResults(2),sprintf('%d-QAM LLR Comparison',simResults(2).M))
else
    load('llrnetQAMPerformanceComparison.mat', 'simResults')
    for p=1:length(simResults)
        llrnetPlotLLR(simResults(p),sprintf('%d-QAM LLR Comparison',simResults(p).M))
    end
end

DVB-S.2 のパケットエラーレート

DVB-S.2 システムでは、軟復調器を使用して LDPC 復号化器に対する入力を生成します。厳密な LLR、近似 LLR、および LLRNet のそれぞれで、関数 llrNetDVBS2PER を使用して、DVB-S.2 システムのパケットエラーレート (PER) を 16-APSK 変調と 2/3 の LDPC 符号でシミュレートします。この関数は、comm.PSKDemodulatorSystem object™ と関数dvbsapskdemodを使用して厳密な LLR と近似 LLR の値を計算し、comm.AWGNChannelSystem object を使用してチャネルをシミュレートします。

simulateNow を true に設定 (またはドロップダウンで [Simulate] を選択) し、関数 llrnetDVBS2PER を使用して subsystemType、EsNoValues、および numSymbols の値の PER シミュレーションを実行します。Parallel Computing Toolbox™ がインストールされている場合、この関数ではparforコマンドを使用してシミュレーションが並列に実行されます。シミュレーション時間は、Intel® Xeon® W-2133 CPU @ 3.6GHz でサイズが 6 の並列プールでのコードの実行 (Parallel Computing Toolbox)を実行した場合で約 40 分です。simulateNow を false に設定 (またはドロップダウンで [Plot saved results] を選択) して、subsystemType='16APSK 2/3'、EsNoValues=8.6:0.1:8.9、および numSymbols=10000 の値の PER の結果を読み込みます。

trainNow を true に設定 (またはドロップダウンで [Train LLRNet] を選択) し、与えられた subsystemType および numSymbols に対する EsNoValues の各値を LLR ニューラルネットワークに学習させます。Parallel Computing Toolbox がインストールされている場合は、オプションの名前と値のペア 'useParallel' を 'yes' に設定して関数 train を呼び出すことでシミュレーションを並列に実行できます。シミュレーション時間は、Intel Xeon W-2133 CPU @ 3.6GHz でサイズが 6 の並列プールでのコードの実行 (Parallel Computing Toolbox)を実行した場合で約 21 分です。trainNow を false に設定 (またはドロップダウンで [Use saved networks] を選択) して、subsystemType='16APSK 2/3' および EsNoValues=8.6:0.1:8.9 についての学習済みの LLR ニューラルネットワークを読み込みます。

DVB-S.2 の PER シミュレーションの詳細については、DVB-S.2 リンク (Simulink での LDPC 符号化を含む)の例を参照してください。ネットワークの学習の詳細については、関数 llrnetTrainDVBS2LLRNetwork および [1] を参照してください。

simulateNow = false;
if simulateNow
    subsystemType = '16APSK 2/3'; %#ok<UNRCH>
    EsNoValues = 8.6:0.1:8.9;     % in dB
    numFrames = 10000;
    numErrors = 200;
    
    trainNow = false;
    if trainNow && (~strcmp(subsystemType,'16APSK 2/3') || ~isequal(EsNoValues,8.6:0.1:9))
        % Train the networks for each EsNo value
        numTrainSymbols = 1e4;
        hiddenLayerSize = 64;
        llrNets = llrnetTrainDVBS2LLRNetwork(subsystemType, EsNoValues, numTrainSymbols, hiddenLayerSize);
    else
        load('llrnetDVBS2Networks','llrNets','subsystemType','EsNoValues');
    end
    
    % Simulate PER with exact LLR, approximate LLR, and LLRNet
    [perLLR,perApproxLLR,perLLRNet] = llrnetDVBS2PER(subsystemType,EsNoValues,llrNets,numFrames,numErrors);
    llrnetPlotLLRvsEsNo(perLLR,perApproxLLR,perLLRNet,EsNoValues,subsystemType)
else
    load('llrnetDVBS2PERResults.mat','perApproxLLR','perLLR','perLLRNet',...
        'subsystemType','EsNoValues');
    llrnetPlotLLRvsEsNo(perLLR,perApproxLLR,perLLRNet,EsNoValues,subsystemType)
end

この結果が示しているように、LLRNet では対数や指数などの計算量の多い演算を使用しなくても厳密な LLR とほぼ同じ性能が得られます。

その他の調査

DVB-S.2 システムの別の変調および符号化方式を試します。変調タイプと符号化率のすべてのリストについては、DVB-S.2 リンク (Simulink での LDPC 符号化を含む)の例を参照してください。ネットワークの隠れ層のサイズを変えて演算数を少なくし、厳密な LLR と比較した場合の性能の低下を測定することもできます。

この例で使用している補助関数は次のとおりです。実装の詳細については、それぞれのファイルを参照してください。

llrnetDVBS2PER.m: 厳密な LLR、近似 LLR、および LLRNet LLR を使用して DVB-S.2 の PER をシミュレートする
llrnetTrainDVBS2LLRNetwork.m: DVB-S.2 の LLR 推定のためのニューラルネットワークの学習を行う
llrnetQAMLLR.m: M-ary QAM の LLR 推定のためのニューラルネットワークの学習を行って厳密な LLR、近似 LLR、および LLRNet LLR を計算する
llrnetNeuralNetwork.m: LLR 推定のための浅層ニューラルネットワークを構成する

参考文献

[1] O. Shental and J. Hoydis, ""Machine LLRning": Learning to Softly Demodulate," 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 2019, pp. 1-7.

LLR 推定用のニューラル ネットワークの学習とテスト