量子化
量子化は、実質的にアナログ信号をデジタル化するプロセスです。このプロセスでは、一定の範囲で区切られた各分割に含まれる入力サンプル値をそれぞれ異なる共通値にマッピングします。量子化マッピングには、"分割" と "コードブック" が必要です。入力信号をスカラー量子化信号にマッピングするには、quantiz 関数を使用します。
パーティションの表現
量子化の分割は、実数値の集合において、オーバーラップしないで隣接する値の範囲を定義します。分割を指定するには、異なる範囲の明確な端点をベクトルでリストします。
たとえば、分割が実数線を次の 4 つの集合 ("区間") に分割する場合を考えてみます。
{x: x ≤ 0}
{x:0 < x ≤ 1}
{x:1 < x ≤ 3}
{x:3 < x}
この場合、分割を 3 要素のベクトルとして表すことができます。
partition = [0,1,3];
分割ベクトルの長さは、分割区間数よりも 1 小さくなります。
コードブックの表現
コードブックは、分割ベクトルによって定義される一意の区間に分類される入力に割り当てる共通の値を量子化器に指定します。コードブックは、長さが分割の区間の数と同じベクトルとして表されます。以下に例を示します。
codebook = [-1, 0.5, 2, 3];
このベクトルは、分割ベクトル [0,1,3] に対して考えられるコードブックの 1 つです。
各入力サンプルの量子化区間の決定
この例では、量子化区間を決定するため、quantiz関数によって返される index ベクトルと quants ベクトルを調べます。index ベクトルは、各入力サンプルについて入力分割ベクトルで指定された量子化区間を示し、quants ベクトルは、入力サンプルを入力コードブック ベクトルで指定された量子化値にマッピングします。
指定された partition で quantiz 関数を使用してデータ セットを量子化し、返されたベクトルの index を調べます。codebook 入力を指定せずに quantiz を実行すると、この関数は、partition の値に基づいて codebook の量子化値を割り当てます。
data = [2 9 8]; partition = [3,4,5,6,7,8,9]; index = quantiz(data,partition)
index = 1×3
0 6 5
partition によって次のように指定されているため、入力データのサンプル [2 9 8] を示す index ベクトルは、0、6、5 のラベルが付いた区間に含まれます。
区間 0 は、3 以下の実数で構成される。
区間 6 は、8 より大きく 9 以下の実数で構成される。
区間 5 は 7 より大きく 8 以下の実数で構成される。
この例において、コードブック ベクトルを次のように定義するとします。
codebook = [3,3,4,5,6,7,8,9];
次の式は、ベクトル index を量子化された信号 quants に関連付けます。
quants = codebook(index+1)
quants = 1×3
3 8 7
この quants の式は、codebook ベクトルを入力して quants ベクトルを返す場合に quantiz 関数が使用するものとまったく同じです。返されたベクトル quants を調べ、codebook ベクトルで定義されているように、partition ベクトル間隔 [0 6 5] が量子化値 [3 8 7] にマッピングされていることを確認します。
partition = [3,4,5,6,7,8,9]; codebook = [3,3,4,5,6,7,8,9]; [index,quants] = quantiz(data,partition,codebook)
index = 1×3
0 6 5
quants = 1×3
3 8 7
サンプリング後の正弦波の量子化
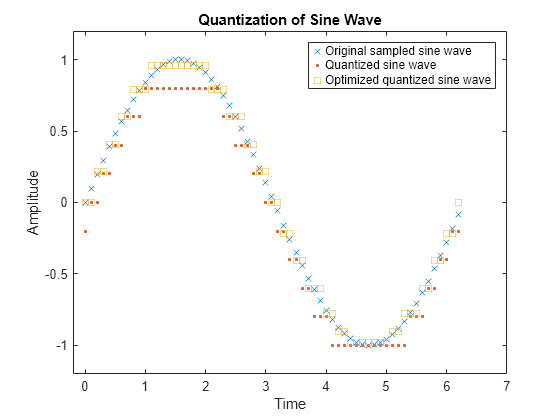
スカラー量子化の性質を説明するために、この例では正弦波を量子化する方法を示します。元の信号と量子化された信号をプロットして、正弦曲線を構成する x 個のシンボルと、量子化された信号を構成するドットを対比させます。各ドットの垂直座標は、ベクトル コードブック内の値です。
t で定義された時間にサンプリングされた正弦波を生成します。間隔が異なる個別のエンドポイントをベクトル要素の値として定義することにより、partition 入力を指定します。partition ベクトルで定義された各間隔の要素の値をもつ codebook 入力を指定します。コードブック ベクトルは、分割ベクトルより 1 要素長くなければなりません。
t = [0:.1:2*pi]; sig = sin(t); partition = [-1:.2:1]; codebook = [-1.2:.2:1];
サンプリング後の正弦波で量子化を実行します。
[index,quants] = quantiz(sig,partition,codebook);
量子化された正弦波とサンプリング後の正弦波をプロットします。
plot(t,sig,'x',t,quants,'.') title('Quantization of Sine Wave') xlabel('Time') ylabel('Amplitude') legend('Original sampled sine wave','Quantized sine wave'); axis([-.2 7 -1.2 1.2])

量子化パラメーターの最適化
大きな信号の集合に対し、微細な量子化方式を使用してパラメーターのテストや選択を行うのは手間のかかる作業です。分割パラメーターとコードブック パラメーターを簡単に生成する方法の 1 つは、一連の "学習データ" に従ってそれらを最適化することです。学習データは、量子化する典型的な種類の信号でなければなりません。
この例では、lloyds関数を使用して、Lloyd アルゴリズムに従って分割およびコードブックを最適化します。このコードは、おおまかな初期推定から開始して、正弦波信号の 1 区間の分割とコードブックを最適化します。この例では、次に、quantiz関数を 2 回実行し、最初の partition 入力および codebook 入力の値と、最適化された partitionOpt 入力および codebookOpt 入力の値を使用して、量子化されたデータを生成します。この例では、最初の量子化と最適化された量子化の歪みも比較します。
正弦波信号と初期量子化パラメーターの変数を定義します。lloyds 関数を使用して分割とコードブックを最適化します。
t = 0:.1:2*pi; sig = sin(t); partition = -1:.2:1; codebook = -1.2:.2:1; [partitionOpt,codebookOpt] = lloyds(sig,codebook);
初期および最適化後の分割ベクトルとコードブック ベクトルを使用して、量子化された信号を生成します。quantiz関数は、平均二乗歪みを自動的に計算して 3 番目の出力引数として出力します。量子化の平均二乗歪みを初期および最適化後の入力引数と比較して、最適化された量子化値を使用すると歪みがどの程度少なくなるかを確認します。
[index,quants,distor] = quantiz(sig,partition,codebook);
[indexOpt,quantOpt,distorOpt] = ...
quantiz(sig,partitionOpt,codebookOpt);
[distor, distorOpt]ans = 1×2
0.0148 0.0022
サンプリングされた正弦波、量子化された正弦波、および最適化後の量子化された正弦波をプロットします。
plot(t,sig,'x',t,quants,'.',t,quantOpt,'s') title('Quantization of Sine Wave') xlabel('Time') ylabel('Amplitude') legend('Original sampled sine wave', ... 'Quantized sine wave', ... 'Optimized quantized sine wave'); axis([-.2 7 -1.2 1.2])
指数信号の量子化と圧縮
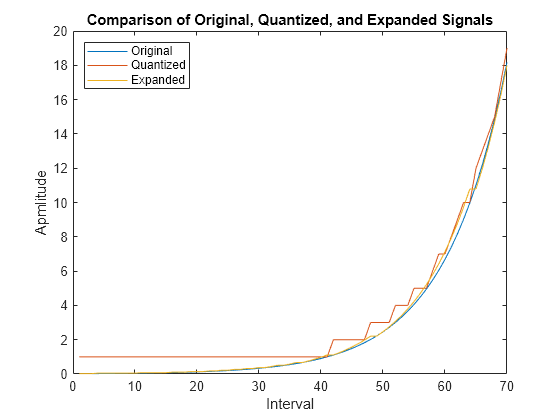
ハイ ダイナミック レンジで信号を送信すると、長さの等しい区間を使用する量子化で信号の歪みと桁落ちが生じる可能性があります。圧伸では、送信側で量子化の前に対数演算を適用して信号を圧縮し、受信側で信号を拡張してフル スケールに戻します。圧伸により、多くの量子化レベルを指定せずに信号の歪みを回避できます。指数信号に 6 ビット量子化を使用したときの歪みを、圧伸を行う場合と行わない場合について比較します。元の指数信号、量子化信号、拡張信号をプロットします。
指数信号を作成してその最大値を計算します。
sig = exp(-4:0.1:4); V = max(sig);
同じ長さの間隔を使用して信号を量子化します。partition 値と codebook 値を設定し、6 ビットの量子化と仮定します。平均二乗歪みを計算します。
partition = 0:2^6 - 1; codebook = 0:2^6; [~,qsig,distortion] = quantiz(sig,partition,codebook);
μ 則方式を適用するように構成した関数 compand を使用して信号を圧縮します。量子化を適用し、量子化した信号を展開します。圧伸した信号の平均二乗歪みを計算します。
mu = 255; % mu-law parameter csig_compressed = compand(sig,mu,V,'mu/compressor'); [~,quants] = quantiz(csig_compressed,partition,codebook); csig_expanded = compand(quants,mu,max(quants),'mu/expander'); distortion2 = sum((csig_expanded - sig).^2)/length(sig);
量子化の平均二乗歪みを、圧伸と量子化を組み合わせた場合の平均二乗歪みと比較します。圧伸して量子化した信号の歪みは、量子化した信号の歪みより 1 桁少なくなっています。長さの等しい区間は指数信号の対数に適していますが、指数信号そのものには適していません。
[distortion, distortion2]
ans = 1×2
0.5348 0.0397
元の指数信号、量子化信号、拡張信号をプロットします。低い信号レベルでの量子化信号エラーを強調表示するため、軸にズームインします。
plot([sig' qsig' csig_expanded']); title('Comparison of Original, Quantized, and Expanded Signals'); xlabel('Interval'); ylabel('Apmlitude'); legend('Original','Quantized','Expanded','location','nw'); axis([0 70 0 20])