compand
μ 則または A 則圧縮器/伸張器による情報源符号化
説明
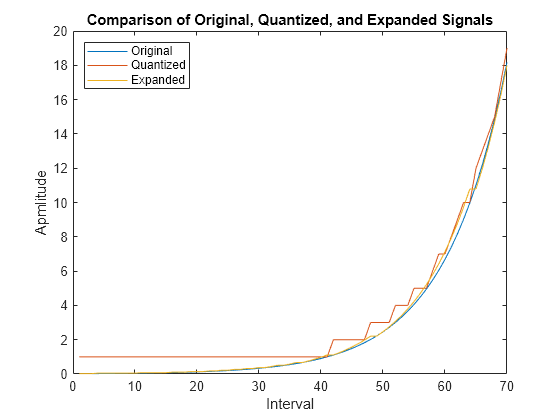
例
入力引数
出力引数
アルゴリズム
音声処理などの用途では、量子化の前に (圧縮器と呼ばれる) 対数演算を使用するのが一般的です。圧縮器の逆演算は、"伸張器" と呼ばれます。圧縮器と伸張器を組み合わせて、"圧伸器" と呼ばれます。
与えられた信号 x に対して、(µ 則) 圧縮器の出力は、以下のようになります。
µ は圧伸器の µ 則パラメーター、log は自然対数、sgn は符号関数 (MATLAB® では sign) です。
入力信号 x の µ 則の伸張は、逆関数 y-1 で求められます。
与えられた信号 x に対して、(A 則) 圧縮器の出力は、以下のようになります。
A は圧伸器の A 則パラメーター、log は自然対数、sgn は符号関数 (MATLAB では sign) です。
入力信号 x の A 則の伸張は、逆関数 y-1 で求められます。
参照
[1] Sklar, Bernard. Digital Communications: Fundamentals and Applications. Englewood Cliffs, NJ: Prentice-Hall, 1988.
バージョン履歴
R2006a より前に導入