硬判定復調と軟判定復調の例

対数尤度比 (LLR) 復調

この例では、畳み込み符号化された通信リンクで硬判定復調の代わりに対数尤度比 (LLR) を使用することで、QPSK 変調に対する BER 性能が向上することを示します。LLR 復調では、ビタビ復号化器を非量子化復号化モードまたは軟判定復号化モードのどちらかで使用できます。非量子化復号化では、復号化器入力は実数値であり、BER の点で優れていますが、現実的には実現不可能です。より現実的な軟判定復号化では、復調器の出力を量子化してから復号化器に送信します。一般に、軟判定復号化により BER のコストが大幅に増大することはなく、むしろ復号化器の複雑度が大幅に低下することが認められます。この例では、シミュレーションを通じて BER 性能を検証します。

この例の Simulink™ バージョンについては、Simulink での LLR と硬判定復調を参照してください。

初期化

シミュレーションパラメーターを初期化します。

M = 4;               % Modulation order
bitsPerIter = 1.2e4; % Number of bits to simulate
EbNo = 3;            % Information bit Eb/No in dB

符号化率 1/2、拘束長 7 コードのコードプロパティを初期化します。

codeRate = 1/2;          % Code rate of convolutional encoder
constLen = 7;            % Constraint length of encoder
codeGenPoly = [171 133]; % Code generator polynomial of encoder
tblen = 32;              % Traceback depth of Viterbi decoder
trellis = poly2trellis(constLen,codeGenPoly);

入力に trellis を使用してcomm.ConvolutionalEncoderSystem object™ を作成します。

enc = comm.ConvolutionalEncoder(trellis);

チャネル

AWGN チャネルに入る信号は、変調され、符号化された信号です。必要なノイズレベルを達成するため、符号化されたビットとマルチビットの各シンボルの Eb/No を調整します。シミュレートする $E_{b} / N_{o}$ 値に基づいて $S N R$ 値を計算します。

SNR = convertSNR(EbNo,"ebno","BitsPerSymbol",log2(M),"CodingRate",codeRate);

ビタビ復号化

それぞれ硬判定、非量子化および軟判定の復号化器として機能するcomm.ViterbiDecoderオブジェクトを作成します。3 つの復号化器すべてについて、トレースバック長を tblen に設定します。

decHard = comm.ViterbiDecoder(trellis,'InputFormat','Hard', ...
    'TracebackDepth',tblen);

decUnquant = comm.ViterbiDecoder(trellis,'InputFormat','Unquantized', ...
    'TracebackDepth',tblen);

decSoft = comm.ViterbiDecoder(trellis,'InputFormat','Soft', ...
    'SoftInputWordLength',3,'TracebackDepth',tblen);

エラーレートの計算

comm.ErrorRateオブジェクトを作成して、復号化されたビットと元の伝送ビットを比較します。ビタビ復号化器は、復号化されたビットストリーム出力に、トレースバック長に等しい遅延を生じさせます。この遅延を考慮に入れるには、comm.ErrorRate オブジェクトの ReceiveDelay プロパティを tblen に設定します。

errHard = comm.ErrorRate('ReceiveDelay',tblen);
errUnquant = comm.ErrorRate('ReceiveDelay',tblen);
errSoft = comm.ErrorRate('ReceiveDelay',tblen);

システムシミュレーション

bitsPerIter の数のメッセージビットを生成します。次に、データを畳み込み符号化および変調します。

txData = randi([0 1],bitsPerIter,1); 
encData = enc(txData);
modData = pskmod(encData,M,pi/4,InputType="bit");

AWGN チャネルを通して、変調された信号を渡します。

[rxSig,nVar] = awgn(modData,SNR);

軟判定モードで comm.ViterbiDecoder オブジェクトを使用する前に、復調器の出力を量子化する必要があります。この例では、SoftInputWordLength が 3 の comm.ViterbiDecoder オブジェクトを使用します。短い語長と少ない BER ペナルティを両立するには、この値が妥当です。3 ビット量子化の分割点を定義します。

demodLLR.Variance = nVar;
partitionPoints = (-1.5:0.5:1.5)/nVar;

受信信号と出力された硬判定ビットを復調します。

hardData = pskdemod(rxSig,M,pi/4,OutputType="bit");

受信信号と出力された LLR 値を復調します。

LLRData = pskdemod(rxSig,M,pi/4,OutputType="llr",NoiseVariance=nVar);

硬判定復号化

復調されたデータをビタビ復号化器を介して渡します。誤り統計を計算します。

rxDataHard = decHard(hardData);
berHard = errHard(txData,rxDataHard);

非量子化復号化

復調されたデータをビタビ復号化器を介して渡します。誤り統計を計算します。

rxDataUnquant = decUnquant(LLRData);
berUnquant = errUnquant(txData,rxDataUnquant);

軟判定復号化

復調されたデータを関数quantizに渡します。軟判定モードでは、ビタビ復号化器は正の数値が 1、負の数値が 0 に相当することを前提とするため、量子化器に渡す前にこのデータを -1 で乗算しなければなりません。量子化器の出力をビタビ復号化器に渡します。誤り統計を計算します。

quantizedValue = quantiz(-LLRData,partitionPoints);
rxDataSoft = decSoft(double(quantizedValue));
berSoft = errSoft(txData,rxDataSoft);

シミュレーション例の実行

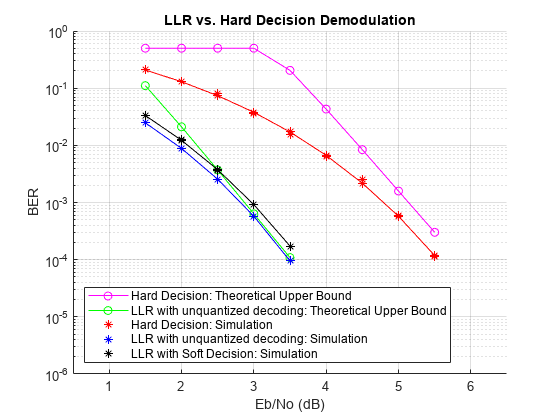
シミュレーションファイル simLLRvsHD を実行し、前述した通信システムを Eb/No 値の範囲全体でシミュレートします。BER を計算し、その結果をプロットします。硬判定復調、非量子化復号化での LLR 復調、および軟判定復号化での LLR 復調の BER 結果はそれぞれ、赤、青、および黒でプロットされます。理論上の結果と比較したシミュレーション結果も表示されます。非量子化復号化の代わりに軟判定復号化を使用することで BER がわずかに低下することを確認します。軟判定復号化の BER 曲線と理論的な限界の BER 曲線との間のギャップは、量子化レベルを上げることで狭めることができます。

この例では BER の結果の計算にある程度時間がかかることがあります。Parallel Computing Toolbox™ (PCT) をインストール済みの場合は、usePCT を true に設定するとシミュレーションを並列実行できます。この場合には、ファイル LLRvsHDwithPCT が実行されます。

範囲の広い Eb/No 値について結果を得るには、適切なサポートファイルを変更します。集計される誤りが多いほど統計的により信頼性の高い結果が得られます。

usePCT = false;
if usePCT && license('checkout','Distrib_Computing_Toolbox') ...
        && ~isempty(ver('parallel'))
    LLRvsHDwithPCT(1.5:0.5:5.5,5);
else
    simLLRvsHD(1.5:0.5:5.5,5);
end

付録

この例では、以下の関数が使用されています。

simLLRvsHD.m — PCT を使用せずにシステムをシミュレートする。
LLRvsHDwithPCT.m — PCT を使用してシステムをシミュレートする。
simLLRvsHDPCT.m — LLRvsHDwithPCT によって呼び出される補助関数。

Simulink での LLR と硬判定復調

この例では次を使用します。

モデルを開く

このモデルでは、畳み込み符号化された通信リンクで、硬判定復調の代わりに対数尤度比 (LLR) を使用すると、BER 性能が向上することを示します。

この例の MATLAB® バージョンについては、対数尤度比 (LLR) 復調を参照してください。

システム設定

このモデル例では、1 つの送信側、1 つの AWGN チャネル、および 3 つの受信側をもつ、畳み込み符号化された通信システムをシミュレートします。畳み込み符号化器の符号化率は 1/2 です。システムでは 16-QAM 変調を採用しています。変調信号は加法性ホワイトガウスノイズチャネルを通過します。一番上の受信側は、硬判定復調を行うように設定されているビタビ復号化器と組み合わせて、硬判定復調を行います。2 番目の受信側には、対数尤度比 (LLR) を計算するように構成されている復調器があり、3 ビットの量子化器を使用して量子化されます。最適な性能を得るには、量子化レベルがノイズ分散に依存していることはよく知られています [2]。量子化器の正確な境界は、ここで経験的に調べます。軟判定復号化を行うように設定されているビタビ復号化器は、これらの量子化された値を処理します。復調器によって計算された LLR 値に -1 を乗算し、ビタビ復号化器で使用する適切な量子化器インデックスに割り当てます。LLR を計算するには、入力時にわかっているノイズ分散を復調器に指定しなければなりません。3 番目の受信側には、非量子化モードで設定されているビタビ復号化器によって処理される LLR を計算する復調器が含まれています。各受信機の BER 性能が計算され、表示されます。

modelName = 'commLLRvsHD';
open_system(modelName);

システムシミュレーションと可視化

さまざまな情報ビットの Eb/No 値にわたって、このシステムをシミュレートします。コードビットおよびマルチビットのシンボルについてこれらの Eb/No 値を調整して、AWGN ブロックおよび Rectangular QAM Baseband Demodulator ブロックに必要なノイズ分散値を取得します。Eb/No 値ごとの BER 結果を収集し、結果を可視化します。

EbNo     = 2:0.5:8; % information rate Eb/No in dB
codeRate = 1/2;     % code rate of convolutional encoder
nBits    = 4;       % number of bits in a 16-QAM symbol
Pavg     = 10;      % average signal power of a 16-QAM modulated signal
snr      = EbNo - 10*log10(1/codeRate) + 10*log10(nBits); % SNR in dB
noiseVarVector = Pavg ./ (10.^(snr./10)); % noise variance

% Initialize variables for storing the BER results
ber_HD  = zeros(1,length(EbNo));
ber_SD  = zeros(1,length(EbNo));
ber_LLR = zeros(1, length(EbNo));

% Loop over all noiseVarVector values
for idx=1:length(noiseVarVector)
    noiseVar = noiseVarVector(idx); %#ok<NASGU>
    sim(modelName);
    % Collect BER results
    ber_HD(idx)  = BER_HD(1);
    ber_SD(idx)  = BER_SD(1);
    ber_LLR(idx) = BER_LLR(1);
end

% Perform curve fitting and plot the results
fitBER_HD  = real(berfit(EbNo,ber_HD));
fitBER_SD  = real(berfit(EbNo,ber_SD));
fitBER_LLR = real(berfit(EbNo,ber_LLR));
semilogy(EbNo,ber_HD,'r*', ...
    EbNo,ber_SD,'g*', ...
    EbNo,ber_LLR,'b*', ...
    EbNo,fitBER_HD,'r', ...
    EbNo,fitBER_SD,'g', ...
    EbNo,fitBER_LLR,'b');
legend('Hard Decision Decoding', ...
    'Soft Decision Decoding','Unquantized Decoding');
xlabel('Eb/No (dB)');
ylabel('BER');
title('LLR vs. Hard Decision Demodulation with Viterbi Decoding');
grid on;

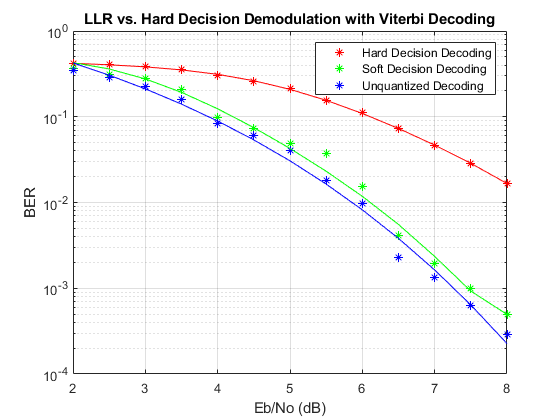
このシステムをさらに実験するには、別の変調タイプを試してください。このシステムでは、より高速で誤りを訂正するためバイナリマッピング方式の変調スキームを使用しますが、グレイマッピング方式の信号コンスタレーションの方が BER 性能が高いことがよく知られています。変調器および復調器のブロック内で、さまざまなコンスタレーション順序オプションで実験します。近似 LLR を計算するように復調器ブロックを構成して、硬判定復調および LLR と比較した BER 性能の違いを調べます。さまざまな Eb/No 値で実験してみます。さらに、変調スキームと Eb/No 値についてさまざまな量子化器の境界を調べます。

Simulink でのデータフローの使用

この例では、Dataflow Subsystem の [領域] パラメーターをデータフローに設定することで、データ駆動型の実行を使用するように構成できます。データフローを使用して、領域内のブロックは、Simulink® のサンプルタイミングではなく使用可能なデータに基づいて実行します。Simulink はシステムをコンカレントスレッドに自動的に分割します。この自動分割はシミュレーションを高速化し、データスループットを増やします。データフローと、複数のスレッドを使用してこの例を実行する方法の詳細については、比較する復調タイプのマルチコアシミュレーションを参照してください。

% Cleanup
close_system(modelName,0);
clear modelName EbNo codeRate nBits Pavg snr noiseVarVector ...
    ber_HD ber_SD ber_LLR idx noiseVar fitBER_HD fitBER_SD fitBER_LLR;

参考文献

[1] J. L. Massey, "Coding and Modulation in Digital Communications", Proc.Int. Zurich Seminar on Digital Communications, 1974

[2] J. A. Heller, I. M. Jacobs, "Viterbi Decoding for Satellite and Space Communication", IEEE® Trans.Comm. Tech. vol COM-19, October 1971