Simulink での LLR と硬判定復調
このモデルでは、畳み込み符号化された通信リンクで、硬判定復調の代わりに対数尤度比 (LLR) を使用すると、BER 性能が向上することを示します。
この例の MATLAB® バージョンについては、対数尤度比 (LLR) 復調を参照してください。
システム設定
このモデル例では、1 つの送信側、1 つの AWGN チャネル、および 3 つの受信側をもつ、畳み込み符号化された通信システムをシミュレートします。畳み込み符号化器の符号化率は 1/2 です。システムでは 16-QAM 変調を採用しています。変調信号は加法性ホワイト ガウス ノイズ チャネルを通過します。一番上の受信側は、硬判定復調を行うように設定されているビタビ復号化器と組み合わせて、硬判定復調を行います。2 番目の受信側には、対数尤度比 (LLR) を計算するように構成されている復調器があり、3 ビットの量子化器を使用して量子化されます。最適な性能を得るには、量子化レベルがノイズ分散に依存していることはよく知られています [2]。量子化器の正確な境界は、ここで経験的に調べます。軟判定復号化を行うように設定されているビタビ復号化器は、これらの量子化された値を処理します。復調器によって計算された LLR 値に -1 を乗算し、ビタビ復号化器で使用する適切な量子化器インデックスに割り当てます。LLR を計算するには、入力時にわかっているノイズ分散を復調器に指定しなければなりません。3 番目の受信側には、非量子化モードで設定されているビタビ復号化器によって処理される LLR を計算する復調器が含まれています。各受信機の BER 性能が計算され、表示されます。
modelName = 'commLLRvsHD';
open_system(modelName);

システム シミュレーションと可視化
さまざまな情報ビットの Eb/No 値にわたって、このシステムをシミュレートします。コード ビットおよびマルチ ビットのシンボルについてこれらの Eb/No 値を調整して、AWGN ブロックおよび Rectangular QAM Baseband Demodulator ブロックに必要なノイズ分散値を取得します。Eb/No 値ごとの BER 結果を収集し、結果を可視化します。
EbNo = 2:0.5:8; % information rate Eb/No in dB codeRate = 1/2; % code rate of convolutional encoder nBits = 4; % number of bits in a 16-QAM symbol Pavg = 10; % average signal power of a 16-QAM modulated signal snr = EbNo - 10*log10(1/codeRate) + 10*log10(nBits); % SNR in dB noiseVarVector = Pavg ./ (10.^(snr./10)); % noise variance % Initialize variables for storing the BER results ber_HD = zeros(1,length(EbNo)); ber_SD = zeros(1,length(EbNo)); ber_LLR = zeros(1, length(EbNo)); % Loop over all noiseVarVector values for idx=1:length(noiseVarVector) noiseVar = noiseVarVector(idx); %#ok<NASGU> sim(modelName); % Collect BER results ber_HD(idx) = BER_HD(1); ber_SD(idx) = BER_SD(1); ber_LLR(idx) = BER_LLR(1); end % Perform curve fitting and plot the results fitBER_HD = real(berfit(EbNo,ber_HD)); fitBER_SD = real(berfit(EbNo,ber_SD)); fitBER_LLR = real(berfit(EbNo,ber_LLR)); semilogy(EbNo,ber_HD,'r*', ... EbNo,ber_SD,'g*', ... EbNo,ber_LLR,'b*', ... EbNo,fitBER_HD,'r', ... EbNo,fitBER_SD,'g', ... EbNo,fitBER_LLR,'b'); legend('Hard Decision Decoding', ... 'Soft Decision Decoding','Unquantized Decoding'); xlabel('Eb/No (dB)'); ylabel('BER'); title('LLR vs. Hard Decision Demodulation with Viterbi Decoding'); grid on;
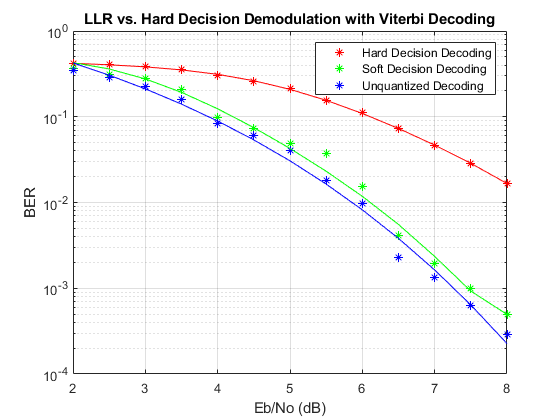
このシステムをさらに実験するには、別の変調タイプを試してください。このシステムでは、より高速で誤りを訂正するためバイナリ マッピング方式の変調スキームを使用しますが、グレイ マッピング方式の信号コンスタレーションの方が BER 性能が高いことがよく知られています。変調器および復調器のブロック内で、さまざまなコンスタレーション順序オプションで実験します。近似 LLR を計算するように復調器ブロックを構成して、硬判定復調および LLR と比較した BER 性能の違いを調べます。さまざまな Eb/No 値で実験してみます。さらに、変調スキームと Eb/No 値についてさまざまな量子化器の境界を調べます。
Simulink でのデータフローの使用
この例では、Dataflow Subsystem の [領域] パラメーターをデータフローに設定することで、データ駆動型の実行を使用するように構成できます。データフローを使用して、領域内のブロックは、Simulink® のサンプル タイミングではなく使用可能なデータに基づいて実行します。Simulink はシステムをコンカレント スレッドに自動的に分割します。この自動分割はシミュレーションを高速化し、データ スループットを増やします。データフローと、複数のスレッドを使用してこの例を実行する方法の詳細については、比較する復調タイプのマルチコア シミュレーションを参照してください。
% Cleanup close_system(modelName,0); clear modelName EbNo codeRate nBits Pavg snr noiseVarVector ... ber_HD ber_SD ber_LLR idx noiseVar fitBER_HD fitBER_SD fitBER_LLR;
参考文献
[1] J. L. Massey, "Coding and Modulation in Digital Communications", Proc.Int. Zurich Seminar on Digital Communications, 1974
[2] J. A. Heller, I. M. Jacobs, "Viterbi Decoding for Satellite and Space Communication", IEEE® Trans.Comm. Tech. vol COM-19, October 1971