このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

モンテカルロ解析によるパラシュートシミュレーション研究

この例では、パラシュート付きの荷物を飛行機から投下するシミュレーションを示します。パラシュートがパッケージから開き、抗力を発生させて降下速度を遅くします。この例では、モンテカルロ解析を使用して、風の乱れ、航空機からの荷物の空中投下高度、およびパラシュートの展開高度の不確実性を考慮したパラシュートシミュレーションの感度調査を実行します。

Simulink モデルの説明

パラシュートシミュレーションアーキテクチャを理解するには、Simulink ™ モデルを開きます。

open_system('ParachuteSim.slx');

最上位モデルは 2 つのサブシステムで構成されています。

環境は、パラシュートが動作する環境を定義します。次のブロックで構成されています。

Flat Earth to LLA ブロックは地球の位置を緯度、経度、高度に変換します。パッケージドロップの初期方位角度と初期緯度および経度は、ブロック内のパラメータとして指定されます。変数 headingInitial は、度単位の初期方位角度に対応します。変数 latInitial と longInitial は、度単位の測地緯度と経度に対応します。

headingInitial    = 45;    
latInitial        = 43.5319;    
longInitial       = 1.2438;

COESA Atmosphere Model は高度に対応する密度値を計算します。
WGS84 Gravity Model は、特定の緯度、経度、高度における地球の重力を計算します。
Wind Shear Model による平均風速の計算、Dryden Wind Turbulence Model (Continuous) による風の乱流の追加、Discrete Wind Gust Model による突風の生成を組み合わせて、リアルな風の環境を作成します。

パラシュートシステムモデルは、6DOF (Euler Angles) ブロックを使用して、初期条件、重量、抗力に基づいてパラシュートモデルをシミュレートします。パラシュートが入った荷物が航空機から落とされると、荷物の重さと空気抵抗の 2 つの力が作用します。パラシュートが開く前は、パッケージの空気抵抗力は無視できるため、パッケージは発射体のような動きをします。パラシュートが開くと、パラシュートの空気抵抗によって降下速度が遅くなります。パラシュートのデフォルト値は、IrvinGQ (旧 Airborne Systems) が製造したフランスのパラシュートの一つである EPC (Ensemble de Parachutage du Combattant) に基づいています。

空気抵抗とパラシュートの重量は反対の力なので、正味の垂直方向の力は重量 $(mass \times g)$ と抵抗力 $(\frac{1}{2} \times rho \times {velocity}^{2} \times C_{d} \times area)$ の差で表されます。ここで、

質量はパラシュートの質量をkgで表します。
gは重力加速度で、9.81 $\frac{m}{s^{2}}$ に近似されます。
rhoは空気の密度で、1.229 $\frac{kg}{m^{3}}$ に近似されます。
速度は $\frac{m}{s}$ のパラシュートの速度に対応します。
$C_{d}$ は抗力係数である
面積は $m^{2}$ におけるパラシュートの面積を表します。

降下中、パラシュートにかかる正味の力がゼロになり、抗力が重量と等しくなる点にすぐに到達します。この関係は、次のようにパラシュートの抗力係数を計算するために使用されます。

area        = 115; 
mass        = 165; 
velocity    = 6;             
g           = 9.81;                      
rho         = 1.229;                      
Cd          = 2*mass*g/(rho*(velocity^2)*area);

環境サブシステムで計算された高度と風速に対応する重力と密度の値は、抗力係数、開高度、パラシュートの質量とともに使用され、パラシュートに作用する正味の力を取得します。変数 hOpening で表される展開高度は、パラシュートがパッケージから展開される高度 (メートル単位) に対応します。開高度は航空機からの空中投下高度よりも低くする必要があることに注意してください。変数 packageMass は、パラシュート付きのパッケージの質量 (kg) に対応します。デフォルトでは、開封高度とパッケージ質量はそれぞれ 500 m と 130 kg に設定されています。

hOpening    = 500;    
packageMass = 130;

パラシュートの正味モーメントはゼロであると仮定します。その後、ネット力とモーメントが 6DOF (Euler Angles) ブロックに入力され、ブロックで指定された初期条件に基づいてパラシュートモデルがシミュレートされます。慣性軸の初期位置は以下のように指定します。変数 ZeInitial は、航空機からの荷物の空中投下高度 (メートル単位) に対応します。デフォルトでは、パッケージの空中投下高度は 2000 m に設定されています。

XeInitial          = 0;  
YeInitial          = 0;   
ZeInitial          = 2000;

x 軸に沿ったパッケージの初期速度は、パッケージが投下されたときの航空機の速度に対応し、デフォルト値は 235 km/h です。y 軸と z 軸に沿ったパッケージの初期速度はゼロ (km/h) と見なされます。初期のオイラー角とオイラー率はゼロと見なされます。3 つのボディ軸の初期速度は、次に示すように convvel 関数を使用して m/s に変換されます。

UInitialKMPH       = 235;     
UInitialMPS        = convvel(UInitialKMPH,'km/h','m/s'); 
VInitialKMPH       = 0;    
VInitialMPS        = convvel(VInitialKMPH,'km/h','m/s'); 
WInitialKMPH       = 0;     
WInitialMPS        = convvel(WInitialKMPH,'km/h','m/s');

パラシュートシミュレーション

デフォルトでは、パラシュートのシミュレーションに風の乱れが導入されます。Discrete Wind Gust Model のパラメータ 突風開始時刻 は突風の開始時刻に対応します。パラシュートが地面に到達するまでの時間は約 100 秒なので、突風開始時間 パラメータに対応する変数 windSeed は、randi 関数を使用して 1 ～ 100 の範囲のランダムな整数として取得されます。風の乱れのないパラシュートモデルをシミュレートするには、windDisturbance 変数を false に設定します。この切り替えは、バリアント選択変数として windDisturbance を持つ Variant Subsystem を使用して Simulink モデルで実行されます。

windDisturbance = true;
if windDisturbance == true
    windSeed = randi(100,1);
end

パラシュートシミュレーションモデルのすべてのパラメータを初期化して設定した後、sim 関数はパラシュートが地面に接触するまでシミュレーションを実行します。結果は、変数 SimResults に Simulink.SimulationOutput オブジェクトとして保存されます。

simResults = sim('ParachuteSim.slx');

シミュレーション結果はパラシュートの応答を特徴づけます。着陸時のパラシュートの状態の概要は以下のとおりです。

パラシュートが地面に着地するまでにかかる時間（秒数）：

TFinal          = simResults.tout(end)

TFinal = 108.3395

パラシュートが地面に当たる x 軸上の位置 (メートル単位):

XeFinal          = simResults.yout{1}.Values.Data(end,1)

XeFinal = 1.1935e+03

パラシュートが地面に当たる y 軸上の位置 (メートル単位):

YeFinal          = simResults.yout{1}.Values.Data(end,2)

YeFinal = -164.5865

パラシュートが地面に衝突するときの x 軸に沿った速度 (m/s):

UeFinal          = simResults.yout{2}.Values.Data(end,1)

UeFinal = -1.9773

パラシュートが地面に衝突するときの y 軸に沿った速度 (m/s):

VeFinal          = simResults.yout{2}.Values.Data(end,2)

VeFinal = -2.8996

パラシュートが地面に衝突するときの z 軸に沿った速度 (m/s):

WeFinal          = simResults.yout{2}.Values.Data(end,3)

WeFinal = -5.1909

変数 YeFinal と VeFinal は風の乱れに依存します。風のない理想的なシナリオを考慮すると、これらの変数はゼロになります。この仮定により、パラシュートは縦方向にのみ動き、x および z 座標で 2D で表されます。ただし、現実的な環境では、パッケージは横方向と縦方向の両方の動きを示し、これは以下に 3D でプロットされています。プロットから、パラシュートが開いて空気抵抗が発生するまで、パッケージが発射体の動きを示していることがわかります。この抗力により降下速度が大幅に低下します。

figure;
plot3(simResults.yout{1}.Values.Data(:,1),simResults.yout{1}.Values.Data(:,2),...
      simResults.yout{1}.Values.Data(:,3));
zlim([0 max(simResults.yout{1}.Values.Data(:,3))]);
grid on;
xlabel('Xe (m)');
ylabel('Ye (m)');
zlabel('Ze (m)');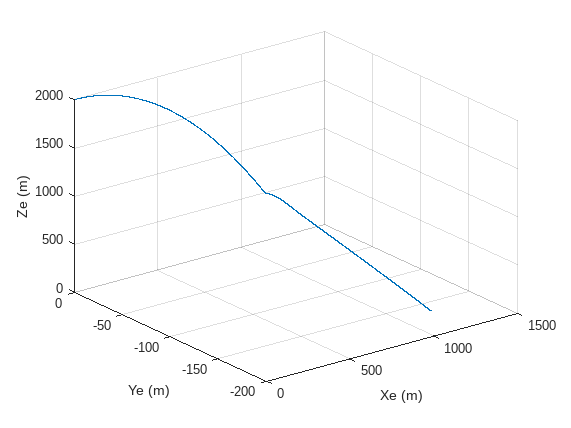

パラシュートシミュレーションの平面衛星ビューを以下に示します。flat2lla 関数は、地球の位置座標から緯度、経度、高度を推定します。geoplot 関数は結果の地理座標をプロットします。geobasemap 関数はベースマップを satellite に変更します。

figure;
llaPosition = flat2lla([simResults.yout{1}.Values.Data(:,1) ...
                        simResults.yout{1}.Values.Data(:,2) ...
                     -1*simResults.yout{1}.Values.Data(:,3)],...
                     [latInitial, longInitial], headingInitial,0);
geoplot(llaPosition(:,1), llaPosition(:,2),'r','LineWidth',2)
geolimits([min(llaPosition(:,1))-0.01 max(llaPosition(:,1))+0.01],...
          [min(llaPosition(:,2))-0.01 max(llaPosition(:,2))+0.01])
geobasemap satellite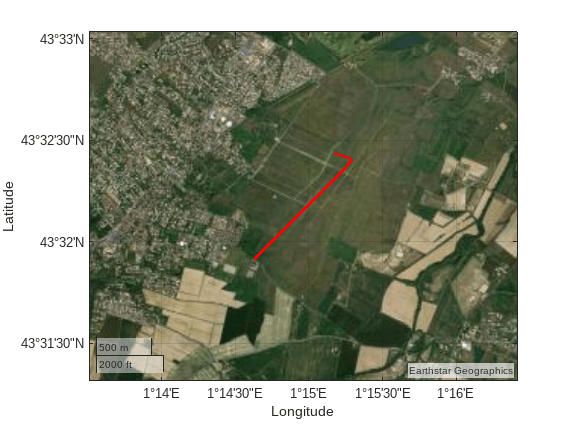

並列シミュレーションを用いたモンテカルロ解析

モンテカルロシミュレーションは、不確実な条件下でのパラシュートの反応を評価します。変数 numSim は、モンテカルロ解析におけるシミュレーションの数を提供します。パラシュートシミュレーションでは、風の乱れ、荷物の空中投下高度、パラシュートの展開高度の不確実性が考慮されます。風の乱れのランダム性は、Discrete Wind Gust Model ブロック内の突風の開始時間を 1 から 100 の範囲で変化させることによって調整されます。

numSim             = 100;
windDisturbance    = true;
gustStartTime      = randi(100,[1 numSim]);

パッケージの空中投下高度とパラシュートの展開高度の不確実性は、それぞれ ZeInitial と hOpening の初期条件に設定された平均値を持つ正規分布曲線に従うと想定されます。空中投下高度と開投高度の標準偏差は以下のように規定されています。

ZeDeviation        = 5;    
hOpeningDeviation  = 5;

次に、randn 関数を使用して、指定された平均と標準偏差を持つ正規分布から、空中投下高度と開高度のランダム値が抽出されます。

airdropAltitude = ZeDeviation.*randn(numSim,1) + ZeInitial;
openingAltitude = hOpeningDeviation.*randn(numSim,1) + hOpening;

モンテカルロ解析ではパラシュートシステムを複数回シミュレートする必要があるため、この例では parsim 関数を使用します。Simulink.SimulationInput オブジェクトは、シミュレーションのさまざまな入力を指定します。parsim 関数は、高速再起動を使用してシミュレーションを実行し、シミュレーションマネージャーを使用して進行状況を監視し、シミュレーションの進行状況を追跡し、Parallel Computing Toolbox ™ を使用してベースワークスペース内の変数を並列ワーカーに転送するように構成されています。

in(1:numSim) = Simulink.SimulationInput('ParachuteSim');
for simNumber = 1:1:numSim
    in(simNumber) = in(simNumber).setVariable('hOpening',openingAltitude(simNumber));
    in(simNumber) = in(simNumber).setVariable('Ze',airdropAltitude(simNumber));
    in(simNumber) = in(simNumber).setVariable('windSeed',gustStartTime(simNumber));
end
simResults = parsim(in, 'UseFastRestart','on','ShowSimulationManager', 'on',...
                    'ShowProgress','on','TransferBaseWorkspaceVariables','on');

[11-Apr-2023 19:39:36] Checking for availability of parallel pool...
Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to parallel pool with 8 workers.
[11-Apr-2023 19:40:30] Starting Simulink on parallel workers...
[11-Apr-2023 19:42:09] Configuring simulation cache folder on parallel workers...
[11-Apr-2023 19:42:10] Transferring base workspace variables used in the model to parallel workers...
[11-Apr-2023 19:42:10] Loading model on parallel workers...
[11-Apr-2023 19:43:32] Running simulations...
[11-Apr-2023 19:45:06] Cleaning up parallel workers...

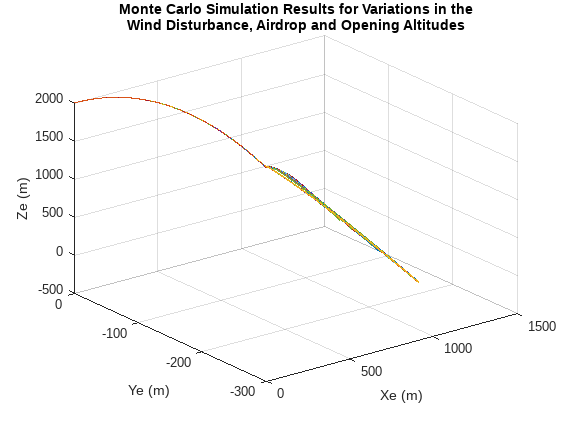
複数のシミュレーションの結果が以下にプロットされています。グラフから、入力の不確実性によってパラシュートの着陸地点にわずかな偏差が生じることがわかります。

figure;
for simNumber = 1:1:numSim
    plot3(simResults(1,simNumber).yout{1}.Values.Data(:,1),...
          simResults(1,simNumber).yout{1}.Values.Data(:,2),...
          simResults(1,simNumber).yout{1}.Values.Data(:,3));
    hold on;
end
grid on;
title(["Monte Carlo Simulation Results for Variations in the";...
       "Wind Disturbance, Airdrop and Opening Altitudes"]);
xlabel('Xe (m)');
ylabel('Ye (m)');
zlabel('Ze (m)');

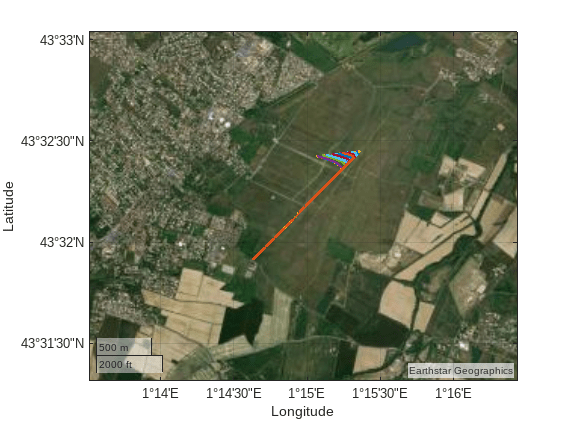
シミュレーション結果は、衛星ビューのジオプロットとしても表示されます。

figure;
gx = geoaxes;
for simNumber = 1:1:numSim
    llaPosition = flat2lla([simResults(1,simNumber).yout{1}.Values.Data(:,1) ...
                            simResults(1,simNumber).yout{1}.Values.Data(:,2) ...
                           -1*simResults(1,simNumber).yout{1}.Values.Data(:,3)],...
                           [latInitial, longInitial], headingInitial,0);
    geoplot(gx,llaPosition(:,1), llaPosition(:,2),'LineWidth',2)
    geolimits(gx,[min(llaPosition(:,1,:))-0.01 max(llaPosition(:,1,:))+0.01],...
                 [min(llaPosition(:,2,:))-0.01 max(llaPosition(:,2,:))+0.01])
    geobasemap(gx,"satellite")
    hold on
end

プロットは、各パラシュートシミュレーションに対応する着陸地点の違いを反映するために拡大表示されます。

figure;
gx = geoaxes;
for simNumber = 1:1:numSim
    llaPosition = flat2lla([simResults(1,simNumber).yout{1}.Values.Data(:,1) ...
                            simResults(1,simNumber).yout{1}.Values.Data(:,2) ...
                         -1*simResults(1,simNumber).yout{1}.Values.Data(:,3)],...
                           [latInitial, longInitial], headingInitial,0);
    geoplot(gx,llaPosition(:,1), llaPosition(:,2),'LineWidth',2)
    geolimits(gx,[43.5375 43.5420],[1.2495 1.2570])
    geobasemap(gx,"satellite")
    hold on
end

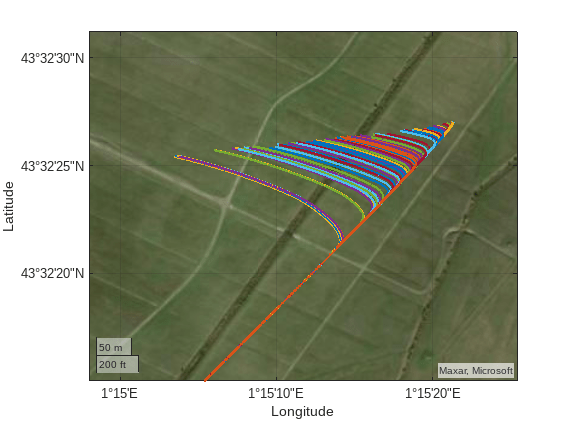
この例では、風の乱れ、空中投下、および開放高度の変化を伴うパラシュートシミュレーションのモンテカルロ解析を示します。突風の開始時間と空中投下および開放高度の標準偏差を変えて、モンテカルロ解析のシミュレーション結果を観察します。

現在のプールを削除

並列プールオブジェクトを使用して、parsim によって作成された並列ワーカーの現在のプールを削除します。

delete(gcp('nocreate'));

Parallel pool using the 'Processes' profile is shutting down.

リファレンス

https://defense-militaire.over-blog.com/2020/12/combien-coutent-les-ensembles-de-parachutage-du-combattant-epc.html