2 次元離散ウェーブレット解析
この節では、Wavelet Toolbox™ ソフトウェアを使用した 2 次元離散ウェーブレット解析の機能について説明します。ツールボックスは、イメージ解析向けに以下の関数を提供します。詳細については、関数リファレンス ページを参照してください。
メモ
この節の説明および例では、インデックス付きイメージ表現に対応する 2 次元配列を使用します。しかし、説明する関数は、トゥルーカラー イメージを使用する場合でも利用できます。これは、m×n×3 の uint8 の配列で表現されます。
解析-分解関数
合成-再構成関数
分解構造ユーティリティ
ノイズ除去と圧縮
関数名 | 目的 |
|---|---|
ウェーブレットによるイメージのノイズ除去 | |
ノイズ除去および圧縮の既定値の提供 | |
ウェーブレットによる 1 次元または 2 次元ノイズ除去のペナルティしきい値 | |
Birgé-Massart 手法を使用した 2 次元ウェーブレットのしきい値 | |
ウェーブレットによるノイズ除去と圧縮 | |
しきい値設定マネージャー |
この節では、次のことを学びます。
イメージを読み込む方法
イメージを解析する方法
イメージを圧縮する方法
ウェーブレットによるイメージの解析と圧縮
この例では、2 次元ウェーブレット解析を使用して、鮮明さを犠牲にすることなく、イメージを効率的に圧縮する方法を示します。
メモ: イメージ I の可視化には、image(I) を直接使用するのではなく、image(wcodemat(I)) を使用します。これは、再スケーリングしたバージョンの I を表示するので、Detail および Approximation をより明確に示すことができます (wcodematを参照)。
イメージを読み込みます。
load porche whos X map
Name Size Bytes Class Attributes X 512x512 2097152 double map 235x3 5640 double
イメージを表示します。
image(X) colormap(map) colorbar
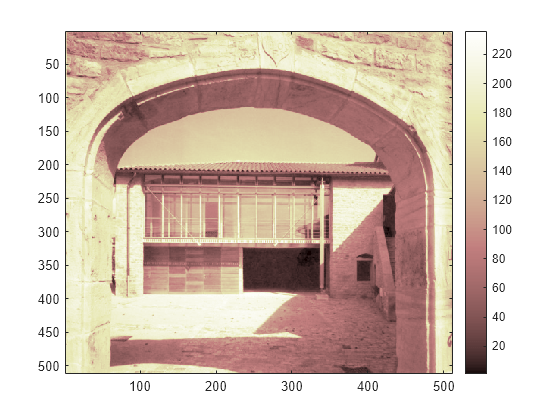
カラーマップが滑らかな場合、ウェーブレット変換をインデックス付きイメージに直接適用できます。そうでない場合、インデックス付きイメージをグレースケール形式に変換する必要があります。詳細については、ウェーブレット: イメージの処理を参照してください。このイメージではカラーマップが滑らかなので、分解を実行できます。
bior3.7 ウェーブレットを使用して、イメージの単一レベル ウェーブレット分解を実行します。係数行列 cA1 は Approximation 係数です。水平方向、垂直方向、対角方向の Detail は、それぞれ行列 cH1、cV1、cD1 に格納されます。
wv = 'bior3.7';
[cA1,cH1,cV1,cD1] = dwt2(X,wv);idwt1 を使用して、係数から Approximation および Detail を構築します (メモ: upcoef2を使うこともできます。)
sx = size(X); A1 = idwt2(cA1,[],[],[],wv,sx); H1 = idwt2([],cH1,[],[],wv,sx); V1 = idwt2([],[],cV1,[],wv,sx); D1 = idwt2([],[],[],cD1,wv,sx);
Approximation と Detail を表示します。
figure tiledlayout(2,2) nexttile image(wcodemat(A1,192)) title('Approximation A1') nexttile image(wcodemat(H1,192)) title('Horizontal Detail H1') nexttile image(wcodemat(V1,192)) title('Vertical Detail V1') nexttile image(wcodemat(D1,192)) title('Diagonal Detail D1') colormap(map)

単一レベルの逆離散ウェーブレット変換によりイメージを再生成します。再生成されたイメージと元のイメージの差は小さいことを確認します。
Xrec = idwt2(cA1,cH1,cV1,cD1,wv); max(abs(X(:)-Xrec(:)))
ans = 1.9895e-13
同じ bior3.7 ウェーブレットを使用して、イメージのレベル 2 ウェーブレット分解を実行します。第 2 レベルの分解のすべての成分 (つまり、第 2 レベルの Approximation と最初の 2 レベルの Detail) の係数は、1 つのベクトル C に連結して返されます。引数 S は、各成分のサイズを記録するブックキーピング行列です。
[c,s] = wavedec2(X,2,wv);
レベル 2 の Approximation 係数を抽出します。第 1 レベルおよび第 2 レベルの Detail 係数を抽出します。
cA2 = appcoef2(c,s,wv,2); [cH2,cV2,cD2] = detcoef2('all',c,s,2); [cH1,cV1,cD1] = detcoef2('all',c,s,1);
レベル 2 の Approximation と レベル 1 およびレベル 2 の Detail を再構成します。
A2 = wrcoef2('a',c,s,wv,2); H1 = wrcoef2('h',c,s,wv,1); V1 = wrcoef2('v',c,s,wv,1); D1 = wrcoef2('d',c,s,wv,1); H2 = wrcoef2('h',c,s,wv,2); V2 = wrcoef2('v',c,s,wv,2); D2 = wrcoef2('d',c,s,wv,2);
Approximation と Detail を表示します。
figure tiledlayout(2,4) nexttile image(wcodemat(A1,192)) title('Approximation A1') nexttile image(wcodemat(H1,192)) title('Horizontal Detail H1') nexttile image(wcodemat(V1,192)) title('Vertical Detail V1') nexttile image(wcodemat(D1,192)) title('Diagonal Detail D1') nexttile image(wcodemat(A2,192)) title('Approximation A2') nexttile image(wcodemat(H2,192)) title('Horizontal Detail H2') nexttile image(wcodemat(V2,192)) title('Vertical Detail V2') nexttile image(wcodemat(D2,192)) title('Diagonal Detail D2') colormap(map)

イメージを圧縮します。ddencmpを使用して既定のパラメーターを計算し、wdencmpを使用して実際の圧縮を実行します。
[thr,sorh,keepapp] = ddencmp('cmp','wv',X); [Xcomp,CXC,LXC,PERF0,PERFL2] = ... wdencmp('gbl',c,s,wv,2,thr,sorh,keepapp);
圧縮後のイメージを元のイメージと比較します。
fprintf('Percentage of wavelet coefficients set to zero: %.4f\n',PERF0);Percentage of wavelet coefficients set to zero: 52.2313
fprintf('Percentage of energy preserved: %.4f\n',PERFL2);Percentage of energy preserved: 99.9982
figure tiledlayout(1,2) nexttile image(X) title('Original Image') axis square nexttile image(Xcomp) title('Compressed Image') axis square colormap(map)

圧縮後のイメージは元の約半数の非ゼロ ウェーブレット係数のみから構成されているにもかかわらず、画質の劣化はほとんど検出できないことがわかります。